Computing Probabilities Of Two Events
Hi there. In this probability post, I will cover the concept of computing probabilities of two events. I cover the keyword and and independent events along with the keyword or and the union of events.

Topics
- The Keyword and & Independent Events
- The Keyword or & Union of Events
- Venn Diagrams For Two Sets
- Practice Problems
- Solutions To Practice Problems
The Keyword and & Independent Events
(I have an earlier post that covers the concept of independent events in probabilities in more detail here.)
When it comes to two or more events in probability the keyword and is similar as to English. In the probability setting, both conditions have to occur at the same time when given the scenario A and B.
Two events A and B are considered when the probability of one event does not affect the probability of the another event.
Let's look at some examples.
Example One
You have ten marbles in a bag. Seven of the ten are red and the remaining three are blue. You pick out two marbles from the bag at random without putting any of the marbles back in the bag. What is the probability that the two marble picks will be both red?
In the first pick, you have a 7 out of 10 chance of picking a red at random.
With the second pick, the number of marbles left in the bag is 9. In addition, there are now 6 red marbles and 3 blue marbles. The probability of picking a second red given that the first pick was a red marble is 6 out of 9.
The probability that the two marble picks are both red is the product of the two fractions.
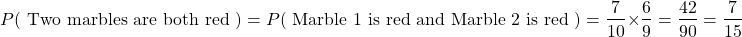
Example Two - Rolling Two Ten Sided Die
When it comes to dice, we are familiar with the common six sided dice. There are also other kinds of dice. For this example, we roll two ten sided dice. You can assume that the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 all have the same chance of showing up on the top of the die.
What is the probability that both ten sided dice have a zero on top?
This question is not too difficult as the two dice are independent from each other when they are rolled. The probability of both dice being zeroes is the product of the individual probabilities.

Example Three - Fair Coin and Spinner
Consider a fair two sided coin with heads and tails along with a spinner with the numbers from 1 to 5. Max flips a coin once and spins the spinner once.
(Spinner Image is a screenshot from ToyTheater website.)
What is the probability of Max flipping a heads and landing an odd number from the spinner?
The probability of flipping a heads is one half. For the spinner, there are three odd numbers out of five from the numbers 1 to 5.
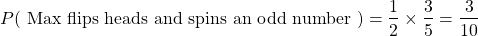
Example Four - Spinner Three Times
The concept of independence and the keyword and can be extended to more than two probability events.
Refer to the above spinner with the numbers 1 to 5 again. What is the probability of spinning all ones in three spins?
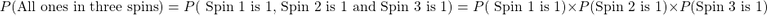
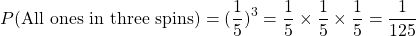

The Keyword or & Union of Events
In the English language the word or means you can only choose one of two choices. When it comes to probability the word or is different. This does confuses newcomers in this topic.
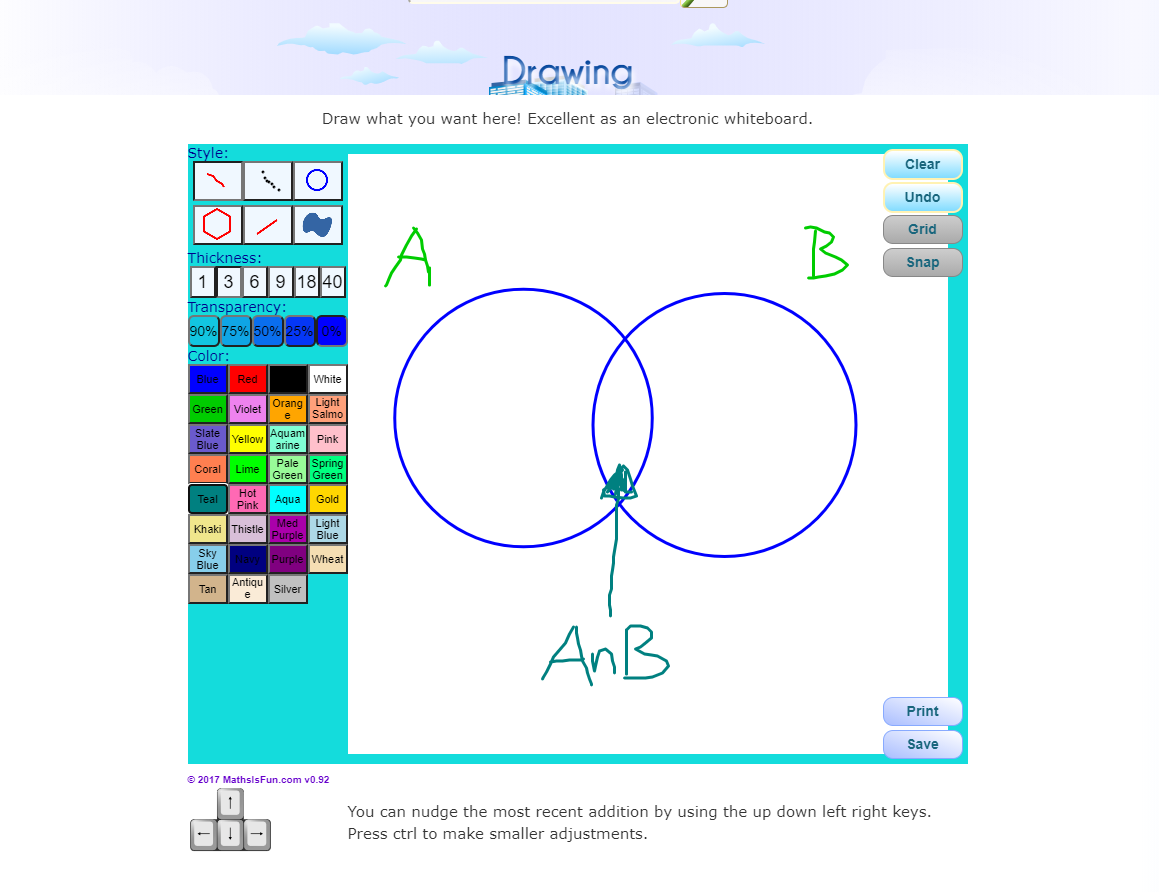
With the A or B or the 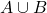 (A Union B) probabilities, consider the cases from the event A and from the event B separately. There might be some overlap between the two events so you have to minus the cases when you have event A and event B at the same time.
(A Union B) probabilities, consider the cases from the event A and from the event B separately. There might be some overlap between the two events so you have to minus the cases when you have event A and event B at the same time.
The explanation from above is better explained with the use of a formula and a Venn diagram for two sets.
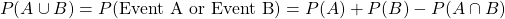
Example One
You flip a fair coin and spin a spinner with the numbers 1 to 5. What is the probability of flipping a tails or landing a 5 from the spinner?
Answer With The Formula Method
Define the event A being flipping a tails and let event B be landing a 5 from the spinner.
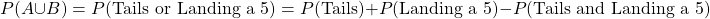
For the probability of landing a tails and landing a five, the concept of independence is used.
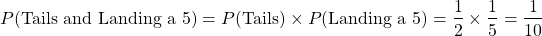
Put all the pieces together to obtain the probability of landing a tails or landing on a 5.
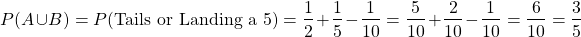
Counting Method
An alternate way of computing the probability of landing a tails or landing on a 5 is through a counting method. We can count the number of cases for tails or for landing on a 5.
Here is a table that lists all the possible ways from the coin flip and spinner.
| Coin Outcome | Spinner Outcome |
|---|---|
| H | 1 |
| H | 2 |
| H | 3 |
| H | 4 |
| H | 5 |
| T | 1 |
| T | 2 |
| T | 3 |
| T | 4 |
| T | 5 |
There are five cases when tails appear from the coin flip. For landing a 5, there are two cases from Tails and 5 and Heads with a 5. But wait. We counted the Tails and 5 case twice though from the flipping a tails alone case and from landing a 5. This is why we subtract one case for the overlap of the Tails and 5 case.
We have 5 + 2 - 1 = 6 cases for a coin being tails or for spinning a 5. This is 6 cases out of 10 possible cases. The answer here is 6 out of 10 or 60%.
Example Two - Roll Of Two Dice
You have two six sided dice and roll both of them. What is the probability that one of the two dice is a 2?
For this question it is best to use the formula. Using a table to list all the possibilities can take time.
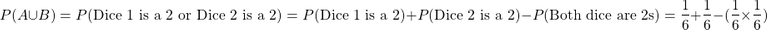

Note
Two probability events are mutually exclusive when the two events cannot happen (impossible) at the same time. The probability of mutually exclusive events is 0.

The probability of event A or event B with mutually exclusive events simplifies to:

Examples of mutually exclusive events include:
- Drawing a King and an Ace in one random card selection from a deck of 52 cards.
- Landing a Heads and Tails on a single coin flip.
- The sum of two dice being a 1 or a 13.
Practice Problems
Peter flips a fair coin three times. What is the probability of all three flips being heads?
Marie spins a wheel twice. The wheel has the numbers 1 to 7. What is the probability that both spins are sevens?
Refer to Marie and the spinner from question 2. What is the probability that one of the spins is a seven?
Noah uses a random number generator which generates a whole number from 1 to 20. What is the probability of the generated number being an even number or a perfect square number. Perfect square numbers include 1, 4, 9, 16, 25 and so on.
Luke claims that flipping a heads from a fair coin and rolling a six from a five sided die are mutually exclusive event. Is Luke correct? Explain your reasoning.

Solutions To Practice Problems
1/8
1/49
13/49
Even number probability is 10/20 or a half. Valid perfect square numbers in this question are 1, 4, 9 and 16. The probability of obtaining a perfect square number is 4 out of 20. From both events, the numbers 4 and 16 are counted twice. The probability of the number being generated being an even number or a perfect square number is 12/20 or 6/10.
Check the probability of flipping a heads on a fair coin and rolling a five. Flipping a heads is one half. Rolling a five is 1 out of 6. The two events are independent so you can take the product of the probabilities. The probability here is 1/12 which is not equal to 0. The two events are not mutually exclusive.

Posted with STEMGeeks
So glad you made it to the trending! I've been learning from your post and because your post, I am going to take math course formally again next month. Keep doing what you do !
Thank you. Which math course are you taking? I assume it would be online correct?
My background is not STEM and I decided to start from 7th grade math 🤣 being in art major for 5 years weaken my math ability. Thanks to crypto I can maintain a bit of it but other than those, yeah I forgot a lot of concept. And yes, it will be conducted online.