Independent Events In Probability
Hello. In this probability post, I cover the concept of independence of probability events. This is taught through examples.
I was planning on putting in some formulas but that might be confusing and would be getting into the territory of probability theory along with some calculus.

Topics
- Independence In Probability Events With Examples
- Practice Problems With Solutions
Independence In Probability Events
Computing the probability of a single random event is nice and all, but when it comes to computing multiple probability events it gets a bit more complicated. The concept of independence in probability occurs when probability events have no effect on each other. This makes probabilities easier to compute with multiple events as the probability of a single trial amongst multiple random trials is the same.

Coin Flipping Example
Consider a two sided fair coin where the probability of heads is 50% and the probability of tails is 50%. A bored person decides to flip the fair coin seven times. The probability of flipping a heads on the first flip is one half, the chance of getting a heads on the second flip is also a half all the way to the probability of flipping a heads on the seventh flip being one half. In each coin flip, there are still two sides to the fair coin.
Flipping the coin on the first try does not affect the probability on the 7th try. We have independence with the probability events as none of the 7 coin flips have any affect on each other. The probability of heads on any of the coin flips is one half.
The probability of all 7 coin flips being all heads would be like this:

Not An Independent Event - Picking Out Three Marbles From A Bag
You have a bag of 12 marbles. Five of the marbles are red, five are blue, one is green and the twelfth marble is yellow.
If you are randomly choosing three marbles from the bag without putting any of the marbles back in the bag, there is no probability independence.
After picking out the first marble, there are 11 marbles left before the second pick. Selecting a second marble from the bag leaves the number of marbles left in the bag from 11 to 10. The third marble pick would be picking one random marble out of 10. As the number of marbles left in the bag changes after each marble pick, we have dependence not independence.
If you want the probability of random selecting 3 blue marbles in three random picks, the calculations would be like this:

Keep in mind that as you pick out a blue marble, the amount of blue marbles available also decreases for the next marble pick.

Example - Multiple Rolls
What is the probability that all five rolls of the single die end up being all ones??
Start with the probability of all seven rolls landing on a one. This is the same as the first roll being a one, second roll is a one to the fifth roll is a one.
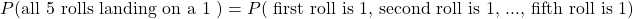
As the rolls do not affect each other, we have the concept of independence for random variables. The right side of the above equality turns into the probability of the first roll being a 1 multiplied by the probability of the second roll being a 1 all the way to the probability of the fifth roll being a 1.
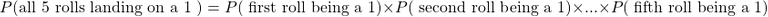
Each roll landing on a one has probability of 1 out of 6. There are five rolls that have a probability of 1 out of 6.
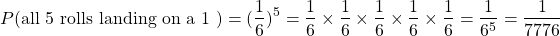

Practice Problems With Solutions
Here are three practice problems with solutions below.
Question One
What is the probability of rolling a three from a fair six sided die four times in four rolls?
Question Two
Develop a formula for the probability of heads from an unfair coin given an unknown amount of coin tosses n. This unfair coin has a probability of heads denoted as h and the probability of tails is q. Note that h is not equal to q but h + q = 1.
Question Three
Consider a random number generator that generates a random 5 digit code. The digit candidates that can be generated are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Repeated digits are allowed in the 5 digit code. What is the probability of the first four numbers being an eight with the last digit being a multiple of 3?
Solutions
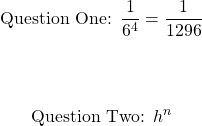
Question Three
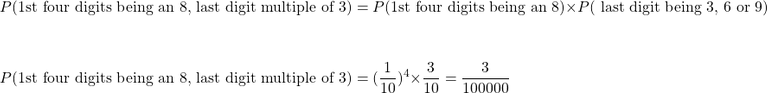

Posted with STEMGeeks
It has been a long, long time since I've taken a statistics course at all, but it was nice to see that my memory was jogged by your explanation, and it made a very great amount of sense. At least to me. Very nicely done!
The problem with this branch of mathematics is its application to places it doesn't belong.
Such as, what is the probability of a sting of coincidences happening?
What is the probability of life forming on this planet?
We see these as random event, when they are anything but.
And finally, the granddaddy of them all, the Schroedinger Experiment
Which was designed to be 50/50, except he failed completely by adding a living component and an emotional component. These make the outcome anything but 50/50.
Hi. I gave your post some thought.
There are cases when probability and mathematics concepts/topics are not used well for real life. Any kind of mathematical/statistical/financial modeling is difficult in my opinion. Simple models are easy to understand for many but don't match well to real life. More complex models match better for real life events and scenarios but are hard to understand.
Model selection requires human decision making which is not always perfect. We do try though to model a representation of a scenario.
I don't do probabilities on coincidences happening nor probabilities of life forming on this planet. I can say that there are events that appear random but are not truly random such as pseudo random numbers from random number generators.
I am not familiar with the Schroedinger Experiment. With that, I have to look into it more closely.