Límites Infinitos y Límites en el Infinito/ Ejemplo de aplicación
En post anteriores hemos tratado el tema de Límites Infinitos y Límites en el Infinito, siguiendo con ese contenido, en el siguiente resolveremos algunos ejercicios de aplicación del tema en cuestión.
Comencemos
Consideremos la siguiente función:
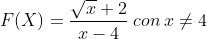.gif)
Como pueden darse cuenta, esta función está definida solo para números reales positivos diferentes de 4 y el 0; es decir, su dominio consiste en el intervalo [0, +∞) - {4}
Estudiemos la función a través de una tabla para los valores de x que se hacen muy próximos a 4 tanto por la izquierda como por la derecha.
Veamos:
| x<4 | F(x) | x>4 | F(x) |
|---|---|---|---|
| 3 | -3,732 | 5 | 4,2360 |
| 3,5 | -7,7416 | 4,5 | 8,2426 |
| 3,9 | -39,7484 | 4,1 | 40,2484 |
| 3,99 | -399,7498 | 4,01 | 400,2498 |
| 3,999 | -3999,749984 | 4,001 | 4000,2499 |
En la tabla se observa que la función F(x) decrece indefinidamente cuando x se aproxima a 4 por la izquierda (x → 4-)
Es decir:
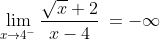.gif)
Razonando similarmente, al observar en la tabla cuando x se aproxima a 4 a través de valores mayores que 4 (x → 4+), podemos concluir que F(x) crece ilimitadamente, en este caso escribimos:
.gif)
A continuación una manera práctica de resolver estos límites:
Partamos del siguiente límite generalizado donde a no está en el dominio de la función racional .gif)
Esto es:
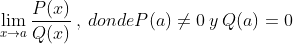.gif)
Entonces:
.gif)
Nota: Recuerde que "a" no está en el dominio de la función y cuando decimos P(a) y Q(a) nos referimos a valores muy próximos a "a" tanto por la izquierda como por la derecha.
De tal forma que en la primera línea se lee que ese límite es igual a " + infinito si P(a) es positivo y Q(a) tiende a 0 a través de valores positivos".
Además, la recta x=a, es una asíntota vertical, es decir, la curva que describe esta función en el plano ℝ2 se acerca infinitamente a esta recta por cualquiera de sus lados (derecha o izquierda) pero jamás la intercepta.
A continuación apliquemos esta regla para resolver el límite anterior:
Iniciamos evaluando el límite, es decir, sustituyendo la variable por el valor al cual tiende la x, en este caso "4", y hagamos los procedimientos correspondientes, así:
.gif)
El resultado de este procedimiento nos da una fracción donde P(4)= 4>0, y el denominador Q(4)= 0; pero recuerden que 4 no está en el dominio de esta función, y que este procedimiento describe solo los signos tanto del numerador como del denominador para valores cercanos a 4 por el lado izquierdo, en este caso escogemos un valor muy próximo a 4 por ese lado, por ejemplo: 3,9 y evaluamos Q(3,9)= 3,9 -4= -0,1; el signo de resultado de Q(3,9) es negativo, por lo cual el signo de 0 es a través de valores negativos, es decir que el resultado de este límite se puede escribir así:
.gif)
Similarmente podemos evaluar el límite de esta función cuando x tiende a 4 por la dercha:
.gif)
Se puede comprobar que el denominador es un número muy próximo a 0 a través de valores positivos (x→0+), ya que al escoger un valor x que cumpla con esta condición, por ejemplo x=4,1, evaluamos Q(4,1)= 4,1-4=+0,1, vemos que el signo de ese resultado es +.
Hagamos ahora que x crezca
Esto es:
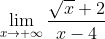.gif)
Para resolver este límite tomemos la función F(x) y multipliquemos tanto el numerador como el denominador por la conjugada del numerador así:
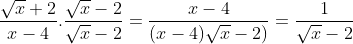.gif)
Ahora nuestro límite quedará así:
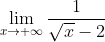.gif)
Evaluemos los límites del numerador y del denoinador por separado, así:
.gif)
Sustituyendo estos valores en el límite anterior nos queda:
.gif)
El lector puede verificar el resultado de este límite a través de la elaboración de una tabla de valores para esta función, donde los valores de x vayan creciendo ilimitadamente. De manera general decimos que 1/∞=0
#Nota: El límite .gif) no tiene sentido para esta función, por cuanto los valores x siempre son positivos, recuerden el dominio de F(x)
no tiene sentido para esta función, por cuanto los valores x siempre son positivos, recuerden el dominio de F(x)
Ahora nos corresponde hacer el bosquejo de la grafica de esta función
Sabemos que y es diferente de 0, ya que y=0 es una asíntota horizontal, y que la gráfica de la función ocupa solo el primer y cuarto cuadrante del Sistema de Ejes Coordenados, ya que no se encuentra definida para x<0.
Para tomar un punto de referencia hagamos x=0, de tal forma que F(0)= -0,5 ¿Por qué?
Teniendo estas referencias y además, considerando que la recta x=4 es una asíntota vertical, podemos bosquejar la gráfica así:
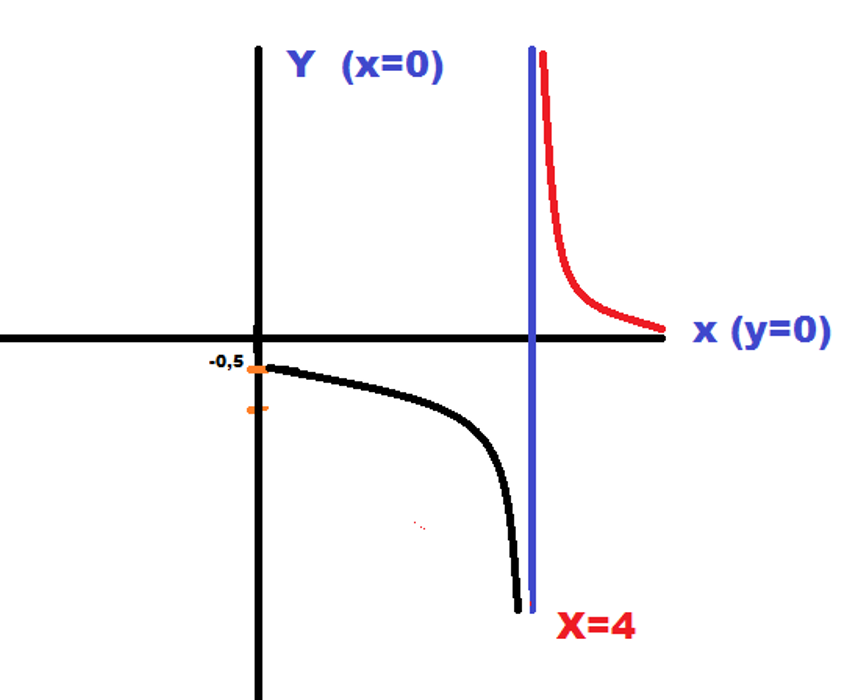
O también, tomar la opción de Desmos Calculadora Gráfica para obtener una gráfica exácta para esta función (eso lo dejamos al lector)
Bueno amigos, hasta aquí el post, espero que sea de agrado y de utilidad para quien lo necesite.
Créditos
Mis soportes técnicos para la realización de este post fueron: Paint y el Editor en Línea de Ecuaciones Latex.
Que bueno la aplicacion con mucha precision y dados ricos!
!1UP
Muchísimas gracias.
You have received a 1UP from @gwajnberg!
@stem-curatorAnd they will bring !PIZZA 🍕
Learn more about our delegation service to earn daily rewards. Join the family on Discord.
PIZZA Holders sent $PIZZA tips in this post's comments:
@curation-cartel(5/20) tipped @analealsuarez (x1)
Please vote for pizza.witness!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @analealsuarez! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s):
Your next target is to reach 10000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Thank you very much.
You're welcome @analealsuarez! Have a nice day 😊👍
Congratulations @analealsuarez! You received a personal badge!
You can view your badges on your board and compare yourself to others in the Ranking
Check out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Dear @analealsuarez, we need your help!
The Hivebuzz proposal already got important support from the community. However, it lost its funding a few days ago when the HBD stabilizer proposal rose above it.
May we ask you to support it so our team can continue its work?
You can do it on Peakd, Ecency, Hive.blog or using HiveSigner.
https://peakd.com/me/proposals/199
All votes are helpful and yours will be much appreciated.
Thank you!