RE: Computation Contest #2 [2 SBI for every participant!]

avatar

You are viewing a single comment's thread:

I am not sure lol. I just looked a the plot and guessed where the first zero is. The convergence is not very good but I got something like 14.13.

import matplotlib.pyplot as plt
def f(y):
    s=complex(0.5,y)
    sum=0
    for i in range(1,10000):
        sum=sum+(i/((i+1)**s))-((i-s)/(i**s))
    return abs(sum)**2


x=[y/10 for y in range(0, 300)]
y=[f(y/10) for y in range(0, 300)]

plt.plot(x, y)
x=14
h=10**-6
for i in range(0,1000):
    temp=f(x)
    df=(f(x+h)-temp)/h
    if(df==0):
        break
    x=x-temp/df
    
print(x)
puzzle stem
0
0
0.000
2 comments
avatar

Altough I am not sure if 14.13 even is a zero :)

0
0
0.000
Reply
avatar
(Edited)

I made another one that works a bit better. The real part seems to always cross the x-axis at a zero(See picture). So the zeros of the real part can easily befound by bisection. Then just check if the imaginary part is 0 aswell :) I got 14.141171601414683 and
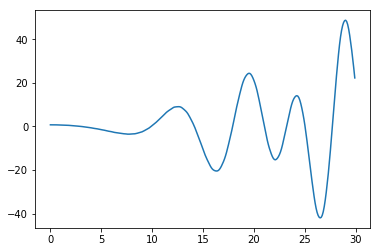
21.025945073366167 as the first 2 zeros.
nn.png

import matplotlib.pyplot as plt
def realf(y):
    s=complex(0.5,y)
    sum=0
    for i in range(1,10000):
        sum=sum+(i/((i+1)**s))-((i-s)/(i**s))
    return sum.real
def imagf(y):
    s=complex(0.5,y)
    sum=0
    for i in range(1,10000):
        sum=sum+(i/((i+1)**s))-((i-s)/(i**s))
    return sum.imag


x=[y/10 for y in range(0, 300)]
y=[realf(y/10) for y in range(0, 300)]

plt.plot(x, y)

candi=[] #Find points with alternating sign
for x in range(0,len(y)-1):
    if(y[x]*y[x+1]<0):
        candi.append([x/10,(x+1)/10])
    
    

for x in candi:
    if(realf(x[0])<0):
        sign=-1
    else:
        sign=1
    x1=x[0]
    x2=x[1]
    tol=1
    while tol>1e-8:
        temp=realf((x1+x2)/2)
        tol=abs(temp)
        if(sign*temp>0):
            x1=(x1+x2)/2
        else:
            x2=(x1+x2)/2
            
            
    if(imagf(x1)<1e-3):        
        print(x1)
0
0
0.000
Reply