Computation Contest #2 [2 SBI for every participant!]

avatar
(Edited)

Here you can solve interesting problems using whatever programming language you like. Also you will earn SBI and sometimes STEM by doing so.
Also you might learn new things by doing so.
The tasks will be rather hard to solve without a programmable computer and some programming skills, but if you want to add a few million numbers by hand or similar, I would still give you the reward.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓

Rules

No upvote, No resteem, No follow required!

I will give 2 SBI for every correct entry.

If two pieces of code are to closely related I might consider the later of them as copied which results in no prize for that person.

You have 4 days to solve it.

Even though this is about computation I will also accept algebraic solutions if you find one.

↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓

Problem

Today I want you to do some numerical stuff.
Consider the following sum:
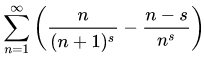
Screenshot from 2019-10-27 20-41-05.png
s is a complex number with
s = 0.5 + yi
The sum does converge for any real y.

Now your task is to use numerical methods to find the smallest value for y > 0 where the sum does converge to 0.

You don't need to be more precise than 3 decimal places.

Tip: The distance between any two consecutive zeros of the sum is generally bigger than 1.

Tip 2(added on @crokkon 's request): There are several 100 zeros between 1 and 1000.

If you don't know complex numbers it would be time to learn about them. They are pretty useful in many cases!

↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓

To everyone who already participated in a past contest, come back today and try a new problem(tell me if you don't want to be tagged):
@crokkon @kaeserotor

In case no one gets a result(which I doubt), I will give away the prize equivalent of one participant to the person who makes the most constructive description why the problem is too hard in your opinion.

↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓

@contrabourdon sponsors my contests with 2 STEEM weekly.
You can support him by using a witness vote on untersatz, so he can further support this and other contests.

puzzle contest sbi steembasicincome programming math stem steemstem steemiteducation palnet
0
0
0.000
7 comments
avatar
(Edited)

.

0
0
0.000
Reply
avatar
(Edited)

Your approach looks pretty good so far.
Yes I want you to find abs(sum) = 0.

Your only problem is that you are are looking at the wrong magnitude and accuracy.
Tip: Between 1 and 1000 are already several 100 zeros.

In general if you approach something like this you need to check roughly first and then go more and more detailed in the regions that contain a change of sign or are close to zero. Especially on complex functions it is useful to look for zeros in real and imaginary part separately.

0
0
0.000
Reply
avatar
(Edited)

.

0
0
0.000
Reply
avatar

You don't necessarily need to get that low. Your results seem good enough.

All that's left to do is to give me the source code.

0
0
0.000
Reply
avatar

I am not sure lol. I just looked a the plot and guessed where the first zero is. The convergence is not very good but I got something like 14.13.

import matplotlib.pyplot as plt
def f(y):
    s=complex(0.5,y)
    sum=0
    for i in range(1,10000):
        sum=sum+(i/((i+1)**s))-((i-s)/(i**s))
    return abs(sum)**2


x=[y/10 for y in range(0, 300)]
y=[f(y/10) for y in range(0, 300)]

plt.plot(x, y)
x=14
h=10**-6
for i in range(0,1000):
    temp=f(x)
    df=(f(x+h)-temp)/h
    if(df==0):
        break
    x=x-temp/df
    
print(x)
0
0
0.000
Reply
avatar

Altough I am not sure if 14.13 even is a zero :)

0
0
0.000
Reply
avatar
(Edited)

I made another one that works a bit better. The real part seems to always cross the x-axis at a zero(See picture). So the zeros of the real part can easily befound by bisection. Then just check if the imaginary part is 0 aswell :) I got 14.141171601414683 and
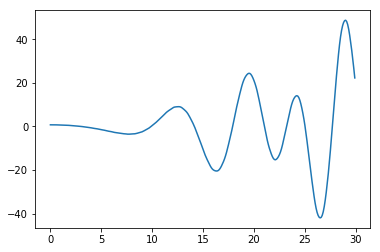
21.025945073366167 as the first 2 zeros.
nn.png

import matplotlib.pyplot as plt
def realf(y):
    s=complex(0.5,y)
    sum=0
    for i in range(1,10000):
        sum=sum+(i/((i+1)**s))-((i-s)/(i**s))
    return sum.real
def imagf(y):
    s=complex(0.5,y)
    sum=0
    for i in range(1,10000):
        sum=sum+(i/((i+1)**s))-((i-s)/(i**s))
    return sum.imag


x=[y/10 for y in range(0, 300)]
y=[realf(y/10) for y in range(0, 300)]

plt.plot(x, y)

candi=[] #Find points with alternating sign
for x in range(0,len(y)-1):
    if(y[x]*y[x+1]<0):
        candi.append([x/10,(x+1)/10])
    
    

for x in candi:
    if(realf(x[0])<0):
        sign=-1
    else:
        sign=1
    x1=x[0]
    x2=x[1]
    tol=1
    while tol>1e-8:
        temp=realf((x1+x2)/2)
        tol=abs(temp)
        if(sign*temp>0):
            x1=(x1+x2)/2
        else:
            x2=(x1+x2)/2
            
            
    if(imagf(x1)<1e-3):        
        print(x1)
0
0
0.000
Reply