La chasse au boson de Higgs - une histoire qui est loin d'être terminée

As always, one sentence for my English-speaking readers. This Thursday post is the French adaptation of this one addressing the past, present and future story of the Higgs boson. The content is globally the same, although I have tried to make it a little bit shorter (I probably exaggerated quite a bit with the English version). But in fact not so much shorter…

Bonjour à tous. C’est jeudi et donc le jour de mon blog hebdomadaire de physique des particules. Avant toute chose, j’annonce que ce post pourrait être le dernier de 2021, vu les vacances scolaires qui s’annoncent dès samedi prochain (en France) et les activités à mettre en place pour mes garçons. Le temps d’écran s’en trouvera ainsi naturellement réduit pour deux semaines. Ceci dit, les nuits sont longues et je dors efficacement. J’arriverai ainsi peut-être à écrire quelque chose, mais sans garantie.

Dans l’article de la semaine dernière, j’ai discuté du travail acharné des physiciens des 100 dernières années, et comment cela a conduit à l’établissement du Modèle Standard de la physique des particules. En essayant de comprendre le fonctionnement de l’univers et l’organisation de la matière, nous sommes arrivés à une théorie basée sur six quarks (up, down, charm, strange, bottom et top), trois leptons chargés (électron, muon et tau) et trois neutrinos (neutrinos électronique, muonique et tau). Ces douze particules élémentaires sont les blocs de base de toute la matière qui nous entoure.

Cette matière n’est bien sûr pas inerte, et elle interagit. Le Modèle Standard inclut trois types d’interaction, à savoir l’électromagnétisme, la force faible et la force forte. Ces interactions sont modélisées à travers le concept de symétries de jauge, dont je ne parlerai pas en détails. Ici, la seule chose à garder à l’esprit est que les particules interagissent via l’échange de médiateurs des forces, dont il existe plusieurs types : le photon (électromagnétisme), les bosons W et Z (interaction faible) et les gluons (interaction forte).

Le succès (à mes yeux totalement non objectifs de physicien) du Modèle Standard est qu’une fois sa vingtaine de paramètres libres fixés, nous pouvons prédire des tonnes de résultats, notamment pour toutes les expériences qui ont eu lieu durant les 100 dernières années. À chaque fois, un excellent accord théorie-donnée est observé (mis à part pour quelques anomalies). Cependant, il y a un souci lié aux symétries de jauge. Par le principe de la définition-même d’une symétrie, tout ce qui n’est pas symétrique est interdit dans la théorie. Et là c’est simple, les particules doivent toutes être non massives. Bien sûr, expérimentalement nous savons que ce n’est pas le cas.

^{[Crédits: CERN]}

Cette problématique est le point de départ de ce blog, qui va discuter du boson de Higgs et du mécanisme de Brout-Englert-Higgs. Ces deux choses ont donné lieu au prix Nobel de physique en 2013, mais il faut savoir que l’histoire du boson de Higgs a démarré dans les années 1960s et se poursuivra encore probablement pendant les 75-100 prochaines années.

Le succès du Modèle Standard

Comme déjà dit plus haut et dans le dernier blog, les symétries de jauge fonctionnent extrêmement bien. Revenons sur ce point une nouvelle fois avant d’aller plus loin.

De façon pratique, la théorie contient une vingtaine de paramètres libres que nous fixons à partir d’un ajustement aux données disponibles. Une fois que cet ajustement est réalisé, on peut ensuite utiliser la théorie (et ses symétries de jauge) pour prédire n’importe quelle quantité pertinente pour une expérience (qui a eu lieu, qui a lieu ou qui aura lieu). L’exemple que j’ai montré dans l’article de la semaine dernière était le ‘brontosaure’ de la collaboration ATLAS (sur cette figure, on peut voir que tous les points de données s’alignent pour nous renvoyer l’image d’un brontosaure…. parfois les physiciens ont des idées étranges, j’avoue).

Un autre excellent exemple vient de ce qui est communément appelé le ‘fit électrofaible’ (ou l’ajustement électrofaible). Ses résultats sont présentés dans la figure ci-dessous.

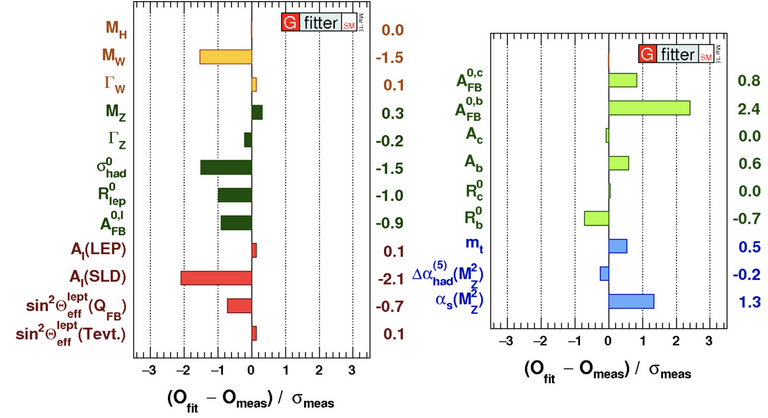
^{[Crédits: GFitter]}

Commençons par expliquer comment cette figure est faite. Tout d’abord, on effectue un fit des paramètres du Modèle Standard à partir des données, en utilisant par exemple un test statistique 𝜒² (ça se lit chi 2). Pour se faire, on prend les mesures expérimentales et les prédictions du Modèle Standard pour un certain nombre de quantités, et on fixe les paramètres pour globalement minimiser les différences entre théorie et données.

Ensuite, on peut comparer les résultats du fit et les données, et quantifier les déviations entre les deux. Ces déviations sont montrées sur la figure : une longue barre colorée indique une grande déviation, et une petite barre colorée indique un bon accord. Mais on peut alors demander de définir grand et petit dans ce contexte. Voyons voir…

Sur la figure, les déviations sont définies comme des déviations standard, ou 𝝈 (il s’agit de la lettre grecque sigma). Le nombre de 𝝈 nous informe sur l’importance d’une déviation.

Afin d’expliquer cela, prenons une pièce de monnaie et jouons 100 fois à pile ou face (si ça vous semble pénible, le pire reste à venir…). On s’attend à avoir grosso modo 50 piles et 50 faces. Mais si on jouait pour de vrai, on pourrait avoir 50 faces, comme 45 faces, 51 faces ou même 70 faces. Au final, tous les résultats sont possibles, mais certains sont plus probables que d’autres.

À présent, entrons dans un délire total et refaisons l’expérience 1000 fois. Et oui, cela donne 1000 fois 100 lancers de pile ou face. Ensuite, imaginons que nous traçons une figure représentant la fréquence d’un certain nombre de faces. On verrait alors que le cas le plus fréquent correspond à 50 faces. Ensuite on aurait 49 et 51. Puis 48 et 52…. et ainsi de suite.

On peut alors définir une déviation standard de 1𝝈 comme la région symétrique autour de 50 telle qu’environ 68% des 1000 résultats y soient inclus. Une déviation de 2𝝈 sera associée à environ 95% des résultats et 3𝝈 à 99.7% des résultats. Ces 1𝝈, 2𝝈 et 3𝝈 sont ce que nous voyons sur l’axe des x de la figure du fit électrofaible. Cela nous permet d’évaluer comment un résultat donné (ou une mesure dans le cas de la physique des particules) est inconsistent avec la théorie (le Modèle Standard). Au plus le nombre de sigmas est grand, au plus grand est le désaccord.

On voit donc sur la figure que chaque mesure correspond à moins de 3 déviations standard, la plupart étant sous le seuil d’un sigma. C’est exactement ce qu’on appelle un excellent accord entre théorie et expérience. En physique des hautes énergies, il faut 3 sigmas pour conclure à la possible existence d’un phénomène nouveau. Il faut ensuite 5 sigmas pour conclure à une découverte. Cela correspond à un pourcentage de 99.99994% dans le vocabulaire ci-dessus. Il y a donc peu de place pour le hasard…

Les origines du boson de Higgs

On a montré pour le moment que le Modèle Standard, et ses symétries de jauge, marchait diaboliquement bien. Mais voilà, s’il y a une symétrie, tous les phénomènes doivent la respecter. Cela implique que la matière est non massive au niveau fondamental. Et là, nous avons quelque chose de non acceptable au vu des données.

Il faut donc résoudre le problème et essayer d’introduire les masses de façon symétrique. Il s’agit d’une idée d’Anderson de 1962, que Brout et Englert (voir ici), et ensuite Higgs (voir ici), ont appliqué à la physique des particules en 1964.

Le mieux pour expliquer cette idée est de prendre l’analogie de la balle au centre d’un bol.

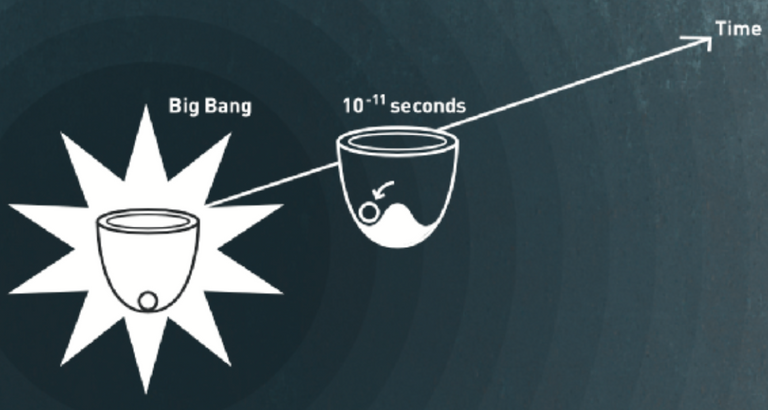
^{[Crédits: Nobel Prize]}

Au tout début de son histoire, l’univers est symétrique. Les symétries de jauge sont réalisées et les particules sont toutes sans masse. Il s’agit de la partie gauche de la figure ci-dessus. Si on pousse un peu la balle à partir du centre du bol, elle y retourne rapidement. La symétrie (de révolution autour de l’axe vertical) est là…

Cependant, 10^-11 secondes après le Big Bang, il se passe quelque chose et on se retrouve avec une bosse au milieu du bol. Cette bosse implique que la balle va tomber dans la vallée en suivant n’importe quelle direction. Ensuite, si on repousse un peu la balle vers le centre, elle retombe rapidement dans la vallée.

Le centre du bol correspond à une position où la symétrie (de révolution autour de l’axe vertical) est réalisée. Cependant, lorsqu’on se retrouve dans la vallée, cette symétrie est cachée du point de vue de la balle.

Il s’agit du mécanisme de Brout-Englert-Higgs. On dit que les symétries de jauge sont brisées spontanément. En fait, nous avons affaire ici à une transition de phase, de la même façon que l’eau peut geler.

La question à 100 HBD est alors : mais quels sont les effets visibles de cette transition de phase ?

La réponse est immédiate : ils nous faut une nouvelle particule, le boson de Higgs. Avant 2012, il nous fallait trouver ce boson. Mais ce n’était pas tout. Trouver un boson de Higgs c’est bien. Trouver le boson de Higgs, avec les bonnes propriétés telles que prédites dans le Modèle Standard, c’est mieux. La première partie de cette quête en deux étapes est de l’histoire ancienne depuis le 4 juillet 2012. Pour la deuxième question, malheureusement nous ne savons pas. La quête reste ainsi ouverte !

À la recherche du boson de Higgs

Le problème de la chasse au boson de Higgs dans les années 1990s est que nous n’avions pas la moindre idée d’où chercher. On rappelle qu’en relativité restreinte, masse et énergie sont équivalentes. Ainsi, la recherche d’un boson de Higgs léger pourra se faire auprès d’expériences mettant en jeu peu d’énergie, et inversement pour un boson lourd. Mais la masse du Higgs pouvait être n’importe quoi, de sorte qu’il était impossible d’estimer la bonne énergie de collision (et tout devait être testé afin d’être sûr de ne rien manquer).

Heureusement, la théorie était là pour nous sauver. Il existait une valeur maximale à la masse du boson de Higgs : 1000 fois la masse du proton. En dessous de cette valeur, tout est cependant permis. On va parler d’une borne supérieure égale à 1000 GeV dans le système d’unités de la physique des particules, 1 GeV étant la masse du proton.

Pour trouver la masse du boson de Higgs (et le boson lui-même tant qu’à faire), on considère une histoire qui a débuté dans les années 1990s avec le Grand Collisionneur Électron-Positron du CERN (le LEP ou Large Electron Positron collider en anglais). Dans cette machine, un faisceau d’électrons et un faisceau de positrons sont accélérés de sorte que des collisions à haute énergie peuvent avoir lieu. Les expériences au LEP ont permis de chercher le boson de Higgs dans des collisions dont l’énergie allait jusqu’à 200 fois la masse du proton.

^{[Crédits: CERN]}

Malheureusement, aucun ‘signal’ n’a été observé. Je reviendrai ci-dessous sur cette notion de signal. Pour le moment, il suffit de considérer qu’il s’agit de la différence entre des prédictions pour une grandeur mesurable avec un boson de Higgs à une masse donnée, et les prédictions correspondantes mais sans boson de Higgs du tout.

L’absence de signal au LEP a permis de rejeter toute hypothèse où la masse du boson de Higgs est fixée à une valeur inférieure à 114 GeV. Au début des années 2000, la masse du boson de Higgs pouvait être ainsi égale à n’importe quelle valeur entre 114 GeV et 1000 GeV.

Le LEP n’est pas le seul à avoir cherché le boson de Higgs. Un autre collisionneur, le Tevatron au Fermilab aux États-Unis, était aussi dans la course à partir des années 1980s jusqu’en 2011. Ici, nous avions des collisions de protons et d’antiprotons.

Bien que l’énergie du Tevatron fut très supérieure (environ 2000 GeV), aucun boson de Higgs ne fut trouvé dans les données. Les physiciens sont alors parvenus à exclure la possibilité d’une masse de Higgs comprise entre 160 et 170 GeV. La quête continuait.

À la fin de la vie du Tevatron, le Grand Collisionneur de Hadrons (Large Hadron Collider en anglais, ou LHC) du CERN a démarré ses activités à une énergie de collision bien plus importante (7000 et 8000 GeV). Fin 2011, la situation est celle schématisée dans la figure ci-dessous. Ici, toute barre colorée correspond à une hypothèse exclue.

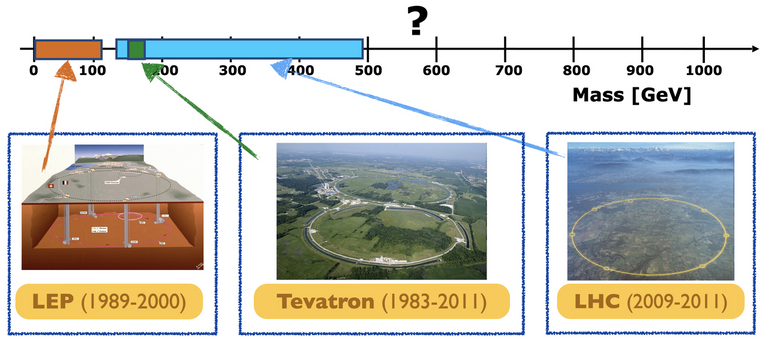
^{[Crédits: @lemouth]}

On peut voir que quasi toute possibilité de boson de Higgs léger est exclue, mis à part quelques valeurs autour de 125 GeV. C’est en fait là que le fameux boson nous attendait…

Le 4 juillet 2012 et après : d’une découverte à aujourd’hui

Le 4 juillet 2012, tout a changé. Les collaborations ATLAS et CMS ont finalement annoncé qu’après toutes ces années, la découverte tant attendue eut lieu !

Pour comprendre comment cela a fonctionné de façon plus pratique, revenons sur cette notion de signal de boson de Higgs. Tout d’abord, rappelons que l’intensité du couplage du boson de Higgs à toute particule est proportionnelle à la masse de la particule. Ainsi, le couplage du Higgs aux particules lourdes (comme le quark top ou les bosons Z et W) est bien plus fort que celui aux particules légères (comme l’électron ou les quarks up et down). Par conséquent, une fois produit, le boson de Higgs aura tendance à se désintégrer plutôt en des particules lourdes.

Ces considérations nous permettent de définir les signatures du boson de Higgs les plus fréquentes, ou autrement dit les meilleures configurations (ou états finaux des processus de collision) à étudier au niveau des détecteurs du LHC. Bien sûr, la sélection des signatures les plus intéressantes prend aussi en compte le bruit de fond du Modèle Standard (c’est-à-dire tous les processus du Modèle Standard donnant lieu au même état final dans le détecteur).

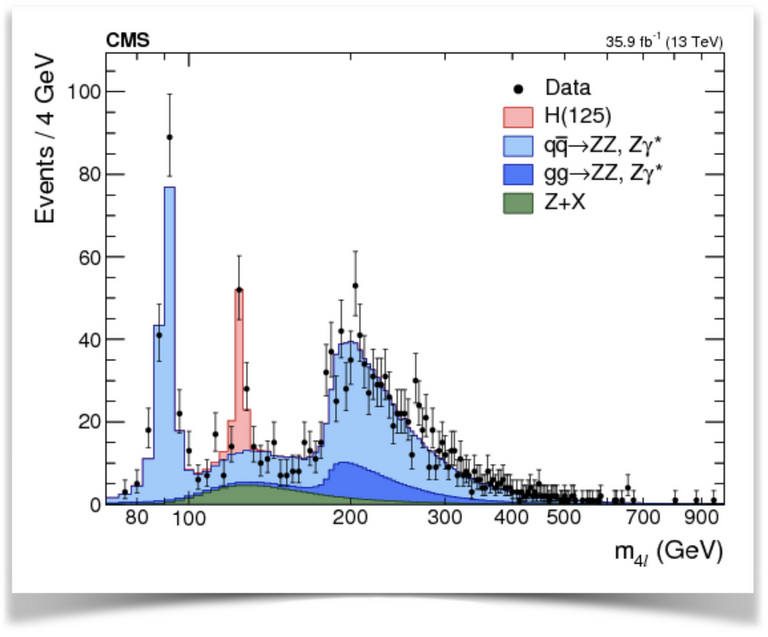
L’idée est de se concentrer sur une signature pour laquelle le signal est relativement fréquent, et le bruit de fond peu important (ou tout au moins réductible). Un exemple est montré dans la figure ci-dessous, sur laquelle sont représentées données et prédictions pour une quantité mesurable spécifique. Le bruit de fond inclut plusieurs processus du Modèle Standard et correspond à la somme des contributions bleue claire, bleu foncée et verte de la figure.

^{[Crédits: CMS collaboration]}

Les données (en noir, avec leurs barres d’erreur) montrent qu’il faut absolument la contribution rouge pour avoir un accord avec la théorie. Cette contribution rouge est le signal d’un boson de Higgs à 125 GeV. Cette figure est en fait la version 2017 de la figure équivalente de 2012 qui a mené à la découverte et au prix Nobel de physique de 2013.

Plein de figures similaires, pour différentes signatures, ont été établies par les physiciens. À chaque fois, les contributions d’un boson de Higgs de 125 GeV sont nécessaires pour obtenir un accord théorie/expérience. En d’autres termes, cela nous permet de conclure à l’existence d’un boson de Higgs de 125 GeV !

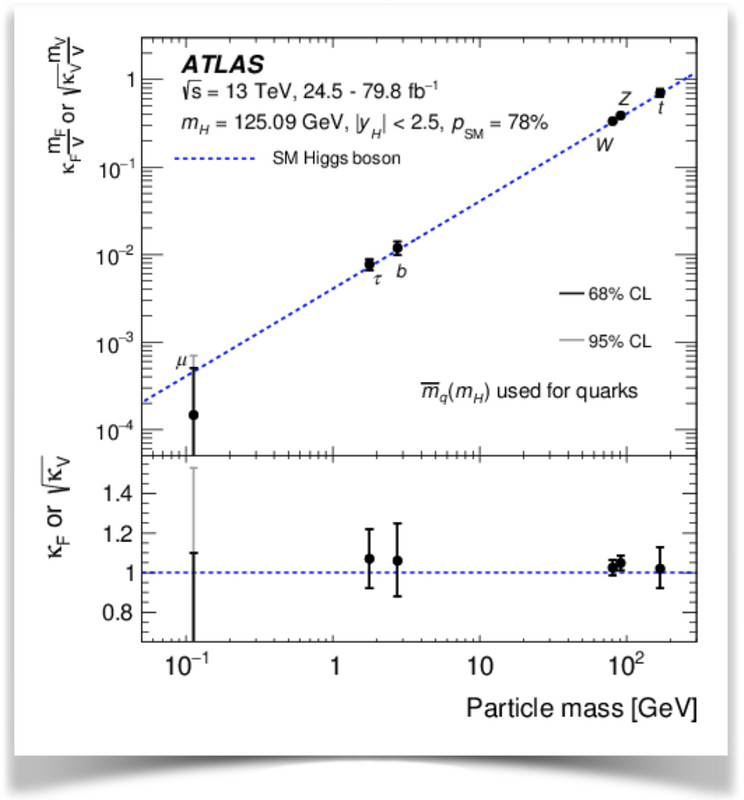
Pour le moment, nous avons discuté de la découverte d’un boson de Higgs. Mais est-ce le boson de Higgs ? Pour ce faire, il faut mesurer les propriétés du boson de Higgs et vérifier qu’elles sont en accord avec les attentes de la théorie. De façon plus pragmatique, il faut mesurer les intensités des couplages du boson de Higgs à chaque particule connue. Et cela a été fait, comme illustré sur la figure ci-dessous (montrant un excellent accord théorie/expérience.

^{[Crédits: ATLAS collaboration]}

Cependant, on peut voir que seuls quelques particules apparaissent sur cette figure : les particules les plus lourdes comme le quark top, les bosons W et Z, le quark bottom, le lepton tau et le muon (même si dans son cas, on a une très grande barre d’erreur). Pour le reste, qui sait…

Ainsi, la quête du boson de Higgs est toujours en cours. Il nous faudra en effet mesurer chaque couplage du boson de Higgs, incluant aussi ses auto-couplages. Ces derniers représentent d’ailleurs un énorme défi pour le LHC et n’importe lequel de ses successeurs.

50 années supplémentaires de chasse au Higgs ?

Il est temps de clore l’écriture de ce blog, car là ça commence à faire un peu long (mais j’ai pris plaisir à raconter tout ça). J’ai voulu partager un petit bout d’histoire sur le sujet du boson de Higgs, retraçant les avancées depuis l’idée théorique jusqu’à sa découverte. Tout a commencé avec le Modèle Standard, ses succès et surtout ses problèmes. Le plus urgent de ces derniers était de pouvoir modéliser les masses des particules. En effet, sans mécanisme de Higgs, les particules fondamentales seraient non massives.

En 2012, la découverte du boson de Higgs a vraiment apporté une pierre conséquente à notre compréhension de l’univers, validant le Modèle Standard (avec le Higgs). Ce n’est cependant pas la fin de l’histoire, car il nous faut à présent vérifier que toutes les propriétés du boson de Higgs sont celles du Modèle Standard.

Le Grand Collisionneur de Hadrons du CERN et les décennies d’analyses qui auront lieu vont nous aider dans cette tâche. Mais cela ne sera pas suffisant. Des collisionneurs plus performants seront nécessaires, et cela garantit d’une certaine façon 100 ans de physique excitante (en tous cas pour les physiciens) !

Après ces 100 années, serons-nous alors capables de dire que le Modèle Standard est complet ? Je ne sais pas, mais il est clair que nous pourrions découvrir sur cette route des phénomènes nouveaux. Ces derniers sont en fait très probables, vu les défauts conceptuels et les limitations du Modèle Standard. Cela sera discuté dans mon prochain post.

Je vous souhaite une bonne fin de semaine à tous et vous donne peut-être rendez-vous jeudi prochain. Sinon ça sera pour 2022 ! N’hésitez bien entendu pas à commenter ou poser des questions.