100 ans de découvertes en physique des particules - le Modèle Standard dans une version 'brique par brique'

For my English-speaking readers, this post is the French version of this one, in which I browse the last 100 years of particle physics history. In fact, the present post is rather an adaptation of its English counterpart. This is indeed needed to have the physics jokes meaning something…

Et voilà, nous sommes jeudi. Et de façon assez incroyable, ma résolution de fin d’année tient toujours : voici un nouveau post de physique des particules. La question à 10 HBD est donc si je vais tenir pour les prochaines semaines…

Concernant le sujet de ce post, il est le fruit d’un débat interne passionné entre moi et moi-même. Je voulais au départ parler des anomalies de saveur, qui sont l’un des sujets brûlants de physique des hautes énergies de ces quelques dernières années. Ces anomalies dans les données, qui sont devenues beaucoup plus solides au vu des résultats récents du Grand Collisionneur de Hadrons du CERN (le LHC), pointent vers des nouveaux phénomènes incompatibles avec le Modèle Standard de la physique des particules. Cependant, il est encore trop tôt pour conclure à une mise en défaut du Modèle Standard, et patience est requise. Autrement dit, le Modèle Standard est toujours le meilleur cadre théorique pour expliquer plus d’un siècle de données en physique des hautes énergies (et prédire les résultats de nombreuses expériences futures).

Mais voilà, la vie n’est pas qu’anomalies, et je me suis dit qu’un article traitant du Modèle Standard de la physique des particules lui-même est en fait plus approprié, vu que cela me permet de planter le décor pour de nombreux futurs posts. Mais pas de panique, je garde les anomalies sous le coude pour janvier !

L’approche que je suis ci-dessous n’est autre que celle que j’utilise lors de mes interactions avec le grand public (comme lors de la Fête de la Science en octobre dernier). Je démarre par une définition de la physique des particules (il faut bien commencer quelque part) et surfe ensuite sur les vagues des développements historiques.

Maintenant que cela est dit, démarrons notre voyage à travers plus de 100 ans de découvertes en physique des particules !

^{[Crédits: CERN]}

---

Qu’est-ce que la physique des particules ?

---

Afin de pouvoir répondre facilement à la question ‘Mais qu’est-ce que la physique des particules’, il est bon de prendre comme point de départ la définition-même du mot ‘physique’. De fait, j’ai ouvert mon Robert (ben quoi ?) à la lettre P. On y trouve une définition présentant la physique comme la science qui étudie les propriétés générales de la matière et qui établit les lois gouvernant tous les phénomènes matériels.

Si on pousse un peu plus loin, on peut appliquer cette définition à la physique des particules. Il suffit de considérer uniquement les entités fondamentales de la matière. La physique des particules essaie alors de déterminer la dynamique des particules élémentaires, c’est-à-dire la façon dont ces dernières vivent leur vie.

Bien sûr, pour comprendre cette dernière phrase précisément, il nous faut définir ces entités fondamentales. Commençons par le faire d’un point de vue un peu bête, celui de l’être humain qui se croit au centre de l’univers (on en connaît tous des spécimens comme ça…). Dans ce contexte, on peut dire que le corps humain est fait principalement d’oxygène, de carbone, d’hydrogène, d’azote, de calcium et de phosphore. Du point de vue de l’univers, cette vision fait un peu rire… Plus de 99.9% de tout ce que l’on observe dans le cosmos est fait d’hydrogène et d’hélium. Le reste des éléments n’apparaît que comme traces infimes. Oui je sais, ça calme et permet de relativiser un peu.

Bien sûr, je ne parle pour le moment que de chimie… et moi et la chimie ça fait 42. J’ai indiqué qu’il fallait deux éléments chimiques pour décrire tout l’univers. Aujourd’hui, nous savons cependant qu’il existe 118 éléments chimiques divers et variés, comme illustré dans le tableau de Mendeleev ci-dessous.

Ce tableau, c’est juste un chaos pas possible. Des atomes partout, tous différents… C’est… mal organisé au final (j’espère que mes collègues chimistes qui liront ce post me pardonneront ce paragraphe).

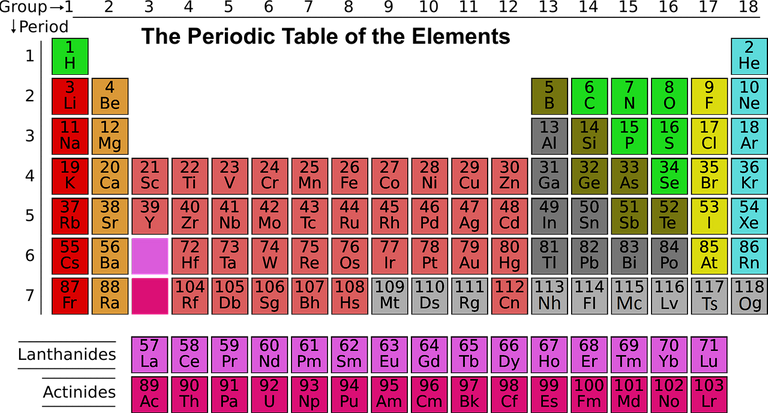
^{[Crédits: Explorersinternational (Pixabay)]}

Profitons-en pour revenir aux physiciens de la première moitié du 20^ème siècle. Ces derniers avaient remarqué que l’ensemble du tableau de Mendeleev pouvait être décrit à partir de seulement trois types d’objet, des protons, des neutrons et des électrons. Il s’agit de ce qui est appelé le modèle de Rutherford. Mais ces trois entités ne sont pas tout. Nous pouvons en effet nous baser sur les premières études de radioactivité pour prendre en compte l’existence d’une quatrième particule, une particule de l’ombre appelée le neutrino.

Ainsi, nous sommes passés de 118 éléments chimiques à quatre particules subatomiques. On aurait même pu dire dans les années 1930 que la physique, c’était une science has been. On a nos quatre particules, et on peut tout expliquer. Basta. L’histoire a heureusement démontré que c’était loin d’être le cas (sinon je ne serais sans doute pas physicien et vous ne me liriez sans doute pas).

---

Les rayons cosmiques et les premiers accélérateurs

---

Reprenons. Nous sommes à présent dans les années 1930-1940 et les physiciens essayaient de comprendre la dynamique du monde microscopique (ce n’est pas très différent d’aujourd’hui). Cependant, contrairement à aujourd’hui, c’était légèrement compliqué par le fait que les accélérateurs n’existaient pas encore. Il fallait alors choisir une autre stratégie : celle des rayons cosmiques de haute énergie.

Lorsqu’un tel rayon cosmique pénètre dans l’atmosphère de la Terre, il va rapidement entrer en collision avec une particule de l’atmosphère. Le résultat de ce processus de collision mène à la création de plusieurs particules secondaires, qui sont toujours très énergétiques. Ces particules vont aussi entrer en collision avec des particules de l’atmosphère, ce qui mènera à encore plus de particules. Et ainsi de suite.

Au final, nous sommes partis d’une particule très énergétique (le rayon cosmique) et on se retrouve avec une gerbe de particules peu énergétiques (appelée une gerbe atmosphérique et illustrée par l’image ci-dessous). À chaque collision, l’énergie d’une particule individuelle baisse, mais nous nous retrouvons avec de plus en plus de particules. Pour comprendre ce qui se trouve dans la gerbe atmosphérique, il suffit alors de se balader avec des émulsions photographiques et attendre que l’on se trouve pile poil là où la gerbe touche le sol.

^{[Crédits: A. Chantelauze, S. Staffi et L. Bret (Pierre Auger Experiment)]}

L’émulsion est simplement une plaque photographique, et cette dernière réagit lorsqu’elle est traversée par des particules chargées. Les trajectoires de ces dernières sont alors enregistrées, et nous pouvons les étudier de près. Cette expérience est extrêmement bon marché, et peut être mise en place plutôt facilement. Le seul problème est la patience. Il est impossible de contrôler quand et où une gerbe atmosphérique aura lieu. Malgré cela, cette stratégie a été très utile, et est à la base de plusieurs découvertes.

Mais heureusement, les choses ont changé dans les années 1940-1950 avec les premiers accélérateurs (comme le Cosmotron au Brookhaven National Laboratory aux États-Unis). À présent, les collisions peuvent être contrôlées. De façon imagée, il suffit de brancher la prise pour envoyer la sauce. Les champs électriques permettent d’accélérer les faisceaux de particules, et les champs magnétiques permettent de contrôler leur trajectoire. On se retrouve alors avec des collisions très énergétiques, pile là où se trouve le détecteur.

Les deux stratégies ci-dessus se basent sur la même physique : la relativité restreinte d’Einstein. Nous avons des collisions à très haute énergie (que cela soit dans l’atmosphère ou en accélérateur). La relativité nous disant qu’énergie et masse sont des grandeurs totalement équivalentes, ces collisions énergétiques pourraient produire de nouvelles particules, plus massives que les quatre qui étaient connues en 1930.

Et c’est exactement ce qui s’est passé. À la fin des années 1950, les physiciens avaient découvert non pas une ou deux, mais des dizaines de nouvelles particules : des pions, des kaons, des 𝛺, des 𝜮, des 𝜩, des 𝜔, des 𝚫, etc. A cela s’ajoutent le muon, un cousin de l’électron assez massif, et le neutrino muonique (le grand frère balourd du neutrino électronique découvert au début du siècle).

Pour résumer, on était de retour à une configuration horriblement chaotique, tout aussi pire que le tableau de Mendeleev.

---

Une vision plus organisée : des quarks au Modèle Standard

---

La situation s’est drastiquement améliorée au milieu des années 1960, quand Gell-Mann et Zweig ont postulé que toutes les particules connues, à l’exception de l’électron, du muon et des deux neutrinos, étaient constituées de deux ou trois particules parmi trois entités fondamentales appelées quarks. Glashow et Bjorken ont alors apporté leur pierre à l’édifice en introduisant un quatrième quark. Toutes les particules connues (sauf l’électron, le muon et les neutrinos qui sont des particules élémentaires appelées leptons) sont alors décrites à partir de quatre quarks, les quarks up, down, étrange et charmé.

Tous les pions, kaons, 𝛺’s, 𝜮’s, 𝜩’s, 𝜔’s, et autres 𝚫’s sont alors organisés en fonction de leur contenu en quarks. Cette classification possédait des propriétés de symétrie, qui démontraient de façon non ambigüe que certaines particules subatomiques étaient manquantes. Cela a donné aux physiciens la possibilité de savoir où chercher de nouvelles particules, et elles ont d’ailleurs été découvertes par la suite.

En 1968, l’idée des quarks a été validée par la découverte de la soustructure du proton au Standard Linear Accelerator Center (SLAC). Le proton n’était plus une particule élémentaire mais un objet composite fait de quarks. C’était dès lors un fait. De façon encore plus géniale, le modèle à quatre quarks a été validé expérimentalement lors de ce que nous appelons la révolution de novembre 1974 (parfois le mot révolution ne sous-entend pas ce que l’on pourrait croire ;) ).

^{[Crédits: CERN]}

Malgré tous ces succès du modèle des quarks, plusieurs observations étaient assez louches au milieu des années 1970. Des particules subatomiques découvertes dans les années 1930-1940, les kaons, étaient à la source d’un problème assez critique. Ces particules sont instables et se désintègrent naturellement après un temps assez court. Cependant, les propriétés observées de ces désintégrations étaient en désaccord avec la théorie.

Une solution élégante à ce problème fut proposée par Harari au milieu des années 1970 : il suffit d’avoir six quarks et non pas quatre. Cela sauvait la théorie, pour autant que ces deux quarks supplémentaires soient découverts. Cela arriva plus tard.

Le cinquième quark, le quark bottom, fut découvert à Fermilab en 1977. Pour le dernier quark, le quark top, il a fallu être beaucoup plus patient. Il fut découvert également à Fermilab, mais en 1995. Ce quark est extrêmement massif, étant une particule élémentaire dont la masse égale celle d’un atome d’or. Cette masse importante lui a permis de se cacher des accélérateurs pendant de nombreuses années. Il a fallu ainsi attendre le développement de machines très puissantes pour pouvoir le produire (cf. la relativité restreinte, la masse étant équivalente à l’énergie).

D’un autre côté, il n’y avait aucune raison d’avoir six quarks et quatre leptons. Tsai a alors supposé l’existence du lepton tau dans les années 1970. Ce dernier fut découvert peu après au SLAC et à Berkeley.

Le dernier neutrino, le neutrino tau, fut très difficile à découvrir. La raison n’est pas sa masse, contrairement au quark top, vu que la masse des trois neutrinos est proche de zéro. Le point important est que les neutrinos sont des particules très faiblement interagissantes, ce qui fait de leur production un processus très rare. De plus, le neutrino tau est lié au lepton tau, ce qui complique la chose fortement. On peut en effet observer facilement un électron ou un muon. Pour un tau, par contre, c’est une autre paire de manches…

Tout ça fait qu’il a fallu attendre juillet 2000 pour que les physiciens de la collaboration DONUT (encore à Fermilab) observent 12 collisions impliquant la production d’un neutrino tau. 12 collisions sur un total de 1000 milliards de collisions qui n’ont rien donné ! C’est donc pire que chercher une aiguille dans une botte de foin… on pourrait plutôt parler de chercher une aiguille dans une botte d’aiguilles…

Le secteur de la matière du Modèle Standard, c’est-à-dire les blocs élémentaires à la base de tous les phénomènes les plus fondamentaux, consistent ainsi en 12 particules : six quarks (up, down, charm, strange, bottom et top), trois leptons chargés (électron, muon et tau) et trois neutrinos (les neutrinos électronique, muonique et tau). Cette conclusion a plus ou moins demandé 70 ans de recherche, la confirmation finale datant de juillet 2000.

---

Les interactions fondamentales

---

Le dernier sujet que je voudrais traiter dans ce post concerne la vie des particules. Nous avons seulement discuté pour le moment ce qu’étaient les particules élémentaires et comment elles avaient été découvertes. Mais quid de leur vie, de leur menu, ou de leurs activités ? En d’autres termes, comment interagissent-elles ?

Dans le Modèle Standard, les interactions sont implémentées au travers de symétries appelées symétries de jauge. Nous avons trois interactions fondamentales : l’électromagnétisme (régissant entre autre l’électricité, le magnétisme et de nombreux phénomènes en chimie ou en biologie pour ne citer que ces exemples), les interactions faibles (liées à la radioactivité et à l’évolution des étoiles) et les interactions fortes (permettant la cohésion des noyaux atomiques comme un tout). Sans entrer dans les détails techniques (c’est légèrement trop pour ce post de blog), les symétries de jauge permettent de modéliser chaque interaction fondamentale par l’échange d’un messager (souvent appelé médiateur) véhiculant l’interaction en question.

Par exemple, des particules chargées interagiront électromagnétiquement en échangeant des photons. Des particules interagiront faiblement par l’échange de bosons W ou Z, et les quarks interagiront fortement en échangeant des gluons.

Cette vision des interactions est-elle la bonne ? La réponse est oui, et pour le démontrer je propose de regarder la figure ci-dessous. On peut y voir une comparaison des prédictions du Modèle Standard (avec ses symétries de jauge) avec les données expérimentales du Grand Collisionneur de Hadrons du CERN.

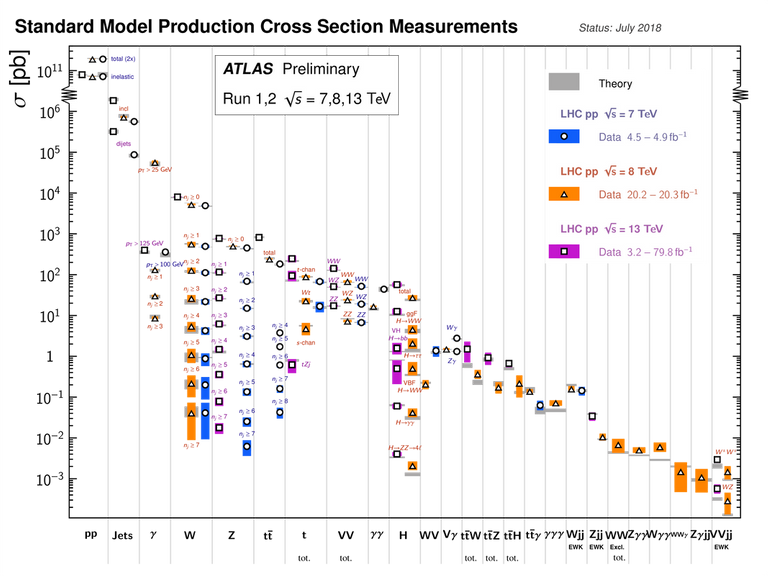
^{[Credits: The ATLAS collaboration (CERN)]}

Chaque marqueur (cercle, carré ou triangle) est associé à un processus spécifique du Modèle Standard (dont la classe générale apparaît sur l’axe x). L’axe vertical correspond au taux de production du processus considéré, ou à sa fréquence. Les processus à gauche sont donc très fréquents et ceux à droite plus rares (et donc plus difficiles à observer car peu communs). Les points de donnée et leur barres d’erreur sont en couleur (orange, bleu, rose) tandis que les prédictions théoriques et leurs barres d’erreur apparaissent en gris.

Cette figure (qui n’est qu’un exemple parmi plein d’exemples) démontre un excellent accord entre théorie et expérience, et ce sur plus de 14 ordres de grandeur ! Et oui, le Modèle Standard marche diaboliquement bien !

---

Et ensuite ?

---

Dans ce post, j’ai introduit le Modèle Standard de la physique des particules d’une façon que je trouve pas mal (et oui c’est très subjectif) lorsque l’on discute de ce sujet avec le grand public. Le fil conducteur part de la définition-même de la physique. Il nous fait ensuite traverser 100 ans de découvertes pour arriver à une théorie contenant 12 blocs de base (six quarks, trois leptons chargés et trois neutrinos) qui interagissent électromagnétiquement, faiblement et fortement (via ces interactions de jauge que j’ai peu décrites).

Cette théorie, le Modèle Standard, est le cadre qui nous permet aujourd’hui d’expliquer du mieux possible comment l’univers fonctionne à son niveau le plus fondamental. À la fin du post, j’ai conclu par une illustration de la puissance de ce cadre théorique en prenant l’exemple du Grand Collisionneur de Hadrons du CERN, le LHC. On peut y voir que le Modèle Standard marche extrêmement bien, et que théorie et données expérimentales sont en excellent accord.

Autrement dit, les physiciens ont accumulé des données riches et variées durant plus de 100 ans, et nous avons à présent une théorie unique capable d’expliquer tout ce qui a été observé. Mais la beauté du Modèle Standard ne s’arrête pas là. Cette théorie est aussi capable de faire des prédictions pour tout ce qui devrait être observé dans les expériences en cours et futures.

C’est après tout la définition-même d’une théorie : il ne s’agit pas de s’ajuster aux données et d’en rester là (ça c’est plutôt un fit), mais bien de fixer une petite quantité de paramètres à partir d’un lot réduit de données pour ensuite être capable de prédire des tonnes et des tonnes de résultats sans changer un iota à nos paramètres et à notre théorie.

Il y a deux choses que je n’ai pas du tout abordées dans ce post.

• Le fameux boson de Higgs découvert il y a environ 10 ans. Cette particule est suffisamment spéciale pour que je garde son histoire pour un autre article (la semaine prochaine, peut-être).
• Mes activités de recherche se placent dans un contexte au-delà du Modèle Standard. Cela veut dire que bien que nous ayons une théorie qui marche super bien, il y a des raisons pour aller au-delà de cette dernière (en la généralisant par exemple). Ces raisons méritent un post complet, et je l’écrirai dans le futur. Il s’agit en effet de la raison d’être de toutes mes recherches.

Je pense à présent que je vais m’arrêter là pour aujourd’hui. J’espère que vous avez eu autant de plaisir à lire ce post que moi à l’écrire. N’hésitez pas à poser des questions, demander des clarifications ou même proposer un sujet dont vous voudriez apprendre plus. Je pense que je serai encore disponible pendant 2 semaines avant de prendre quelques jours de repos en Belgique. Bonne fin de semaine à tous et à jeudi prochain !