À la recherche de neutrinos aux collisionneurs de particules... sans neutrinos !

Dans le post de la semaine dernière, nous avons effectué un premier pas dans le monde des neutrinos, suivant une approche historique menant aux mystères actuels. Ces mystères sont source d’excitation, les neutrinos étant souvent considérés comme portail pour les phénomènes nouveaux au-delà du Modèle Standard de la physique des particules. Ces mystères sont aussi la raison pour laquelle j’ai commencé à travailler sur cette thématique.

Aujourd’hui, j’ai décidé de plonger pleinement dans mes recherches et de vous les présenter. Après un bref résumé de l’épisode précédent, je détaillerai les moyens existants pour percer les secrets des neutrinos. Ensuite, on parlera de mon travail qui a donné lieu à deux publications scientifiques l’an dernier (ici et là). Avec des collaborateurs, nous avons proposé une nouvelle idée pour étudier les neutrinos au Grand Collisionneur de Hadrons du CERN, en utilisant des processus dans lesquels deux leptons (électrons, muons ou taus) de même charge électrique sont produits… sans le moindre neutrino.

N’est-ce pas super cool ? Étudier les neutrinos sans neutrinos ! Les expériences du Grand Collisionneur de Hadrons (le LHC) ont en tout cas trouvé l’idée suffisamment intéressante pour démarrer les analyses expérimentales associées. En attendant que leurs résultats sortent, je vais profiter de ce blog pour vous parler de tout ça.

^{[Crédits: Image originale de KATRIN]}

---

Les neutrinos, ou le côté obscur du Modèle Standard

---

Les neutrinos furent introduits afin de fournir une explication à certains résultats des premières études de radioactivité du début du 20^ème siècle. La conservation de l’énergie est un concept inviolable en physique. Dans toute réaction, l’énergie de l’état initial doit ainsi être égale à l’énergie de l’état final. Dans les processus de désintégration beta où un noyau atomique se désintègre en un autre noyau avec l’émission d’un électron, un déséquilibre dans le budget énergétique émergeait des expériences. Pauli a proposé qu’une particule furtive emportait de l’énergie, de sorte que les résultats farfelus ne venaient que de notre incapacité à détecter toutes les particules de l’état final de la désintégration.

Aujourd’hui, nous avons un Modèle Standard contenant trois types de neutrinos : le neutrino électronique, le neutrino muonique et le neutrino tau. Leurs propriétés sont cependant surprenantes. Ainsi, un neutrino d’un type donné peut se convertir en un neutrino différent lors de sa propagation sur de grandes distances. Par exemple, un neutrino électronique émis par le soleil pourrait être détecté sur Terre comme un neutrino électronique, muonique ou tau, chaque possibilité étant associée à une probabilité donnée.

Un tel mécanisme n’est pas prédit par le Modèle Standard, car il implique que les neutrinos sont massifs. Il nous faut alors généraliser le Modèle Standard en y incluant trois neutrinos massifs qui sont des mélanges des neutrinos électroniques, muoniques et taus de départ. Tout neutrino contient ainsi une certaine quantité de ‘saveur’ électronique, de saveur muonique et de saveur tau. Le but des recherches actuelles est ensuite de mesurer la composition de chaque neutrino, ainsi que sa masse.

^{[Crédits: Reidar Hahn (domaine public)]}

---

Les masses des neutrinos et leurs propriétés

---

Les tests des propriétés des neutrinos se font via de nombreuses expériences. La plupart d’entre elles se concentrent sur les paramètres de mélange, et je ne vais pas en parler spécifiquement. Je vais plutôt me concentrer sur d’autres classes d’expérience.

L’expérience KATRIN a pour but de mesurer le régime absolu des masses des neutrinos à partir de mesures de précision dans des désintégrations beta. Je me répète (il paraît que c’est l’âge), mais il s’agit de processus durant lesquels un noyau atomique se désintègre en un autre noyau par l’émission d’un électron et d’un neutrino invisible.

Si on regarde ce qu’il se passe au niveau des constituants des atomes, un neutron (en bleu ci-dessous) se désintègre en un proton (en rouge ci-dessous), un électron (en orange ci-dessous) et un neutrino (en mauve ci-dessous). La différence de masse entre les deux noyaux mène alors à une certaine quantité d’énergie cinétique partagée entre l’électron et le neutrino.

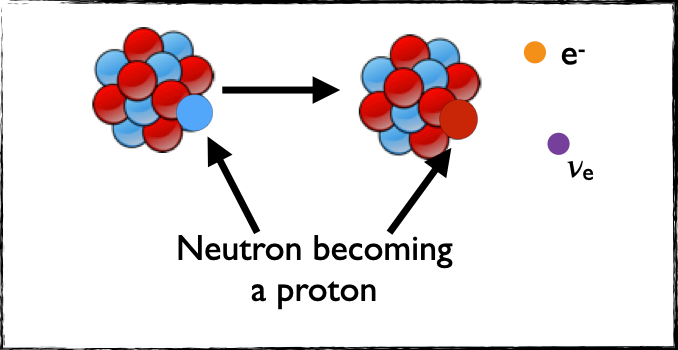
^{[Crédits: @lemouth]}

Nous pouvons calculer comment ce partage d’énergie entre l’électron et le neutrino se fait. Il se trouve que l’électron a une énergie cinétique comprise entre zéro et une certaine valeur maximum. Cependant, cette valeur dépend de la masse des neutrinos, que nous pouvons donc reconstruire par une mesure précise de la distribution en énergie de l’électron.

KATRIN effectue cela à partir de noyaux de tritium (un isotope radioactif de l’hydrogène contenant deux neutrons). En 2019, une borne supérieure de 1.1 eV sur la masse des neutrinos a été obtenue (c’est-à-dire environ un milliardième de la masse du proton). Et ce seulement après quatre semaines de prise de données (voir ici).

KATRIN est toujours en cours, et une limite 5 fois plus faible pourra être atteinte après 1000 jours de prise de données. Là, cela devient carrément intéressant, vu que l’on s’attend à des masses de neutrinos autour de quelques pourcents d’eV.

Cependant, des contraintes bien meilleures proviennent de la cosmologie, Les neutrinos ont en effet laissé leur empreinte dans de nombreuses observables cosmologiques. Par exemple, la somme des masses des neutrinos est un paramètre jouant un rôle dans la formation des grandes structures de l’univers, et il ne peut être arbitraire afin d’avoir un bon accord entre simulations et observations.

L’analyse du fond diffus cosmologique (ou le CMB) mène a une conclusion similaire. Je rappelle que le CMB, aussi connu sous le nom de rayonnement fossile, fournit une photo d’un bébé-univers de 380,000 ans (voir ici). Avant d’avoir eu cet âge nôble, l’univers était composé de matière chargée électriquement (des noyaux atomiques et des électrons). À 380,000 ans, la matière se combine pour former des atomes neutres.

La lumière ne peut cependant voyager sur des grandes distances que dans un environnement neutre. Ainsi, la lumière de l’époque (c’est-à-dire celle présente lorsque l’univers avait 380,000 ans) est toujours là aujourd’hui. C’est ce qu’on appelle le CMB. Nous pouvons étudier ses propriétés. Ces dernières dépendant de la somme des masses des neutrinos, qui peut alors être contrainte indirectement.

^{[Crédits: Pierre Auger Observatory (ESA)]}

Il existe aussi d’autres moyens cosmologiques pour contraindre cette quantité, mais tous mènent à la même conclusion. La somme des masses des trois neutrinos doit être inférieure à 0.26 eV (voir ici).

D’un autre côté, nous pouvons aussi utiliser un tout autre type de processus pour étudier les neutrinos : les désintégrations double-beta sans neutrinos. Ici, un noyau atomique se désintègre en un noyau contenant deux neutrons de moins et deux protons de plus, le tout étant accompagné de l’émission de deux électrons et aucun neutrino.

Ces processus permettent de tester si les neutrinos sont leurs propres antiparticules. Aucune observation ne va dans ce sens pour le moment, mais nous ne pouvons pas encore conclure à l’hypothèse inverse. Ces processus double-beta sans neutrino sont à la base de l’idée que mes collaborateurs et moi avons poursuivie dans un contexte de collisionneur de particules (voir ici).

---

Des processus double-beta sans neutrino aux collisionneurs

---

Afin d’expliquer ce que nous avons fait, je vais me permettre de zoomer un peu sur la désintégration beta durant laquelle un neutron est converti en un proton, un électron et un neutrino. En termes de quarks, un neutron est fait de deux quarks down et un quark up, tandis qu’un proton est fait de deux quarks up et un quark down (voir ici pour quelques détails sur la formation des particules composites à base de quarks).

Dans un processus de désintégration beta, un des quarks down du neutron se transforme en quark up, de sorte que le neutron devient un proton. Cela s’accompagne de l’émission d’un boson W virtuel, vu que cette transformation est liée aux interactions faibles. Ce boson W n’est pas réel car il n’y a pas assez d’énergie relativement à sa masse. Nous pouvons cependant voir son effet via la production d’un électron et d’un neutrino.

L’image ci-dessous illustre la situation. Les quarks up et down sont indiqués par un u et un d, tandis que les protons et neutrons sont représentés par un p et un n. Le quark down du neutron (en bas à gauche) devient le quark up du proton (en haut à gauche), le tout venant avec la création d’un électron et d’un neutrino (à droite).

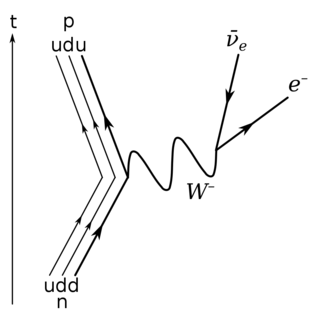
^{[Crédits: Hoel Holdsworth (domaine public)]}

À présent, nous allons brouiller les pistes et compliquer la situation. Parlons de processus double-beta sans neutrino mettant en jeu la désintégration de deux neutrons en deux protons et deux électrons. Comme son nom l’indique, nous allons utiliser un diagramme comme celui ci-dessus… mais deux fois.

• Un premier neutron se désintègre en un proton, un électron et un neutrino. Il s’agit juste d’une désintégration beta normale.
• Un deuxième neutron va interagir avec le neutrino résultant de la première réaction, pour produire un électron et un proton. Ce processus implique les mêmes particules que dans une désintégration beta classique (un neutron, un proton, un électron et un neutrino), mais la nature ‘état final’ et ‘état initial’ du neutrino a été modifiée.

Un processus double-beta sans neutrino consiste donc bien en la désintégration de deux neutrons en deux protons et deux électrons. Aucune trace du moindre neutrino. Avec mes collaborateurs, nous avons eu l’idée d’insérer le processus double-beta dans un contexte de collisionneur, en changeant simplement la nature ‘état final’ et ‘état initial’ des particules impliquées.

Nous avons considéré un processus dans lequel deux protons accélérés émettent deux bosons W qui vont interagir pour produire deux leptons de même charge électrique, via l’échange d’un neutrino entre les deux ‘branches du processus’. Et comme une image vaut 1000 mots, en voici une qui devrait clarifier la situation.

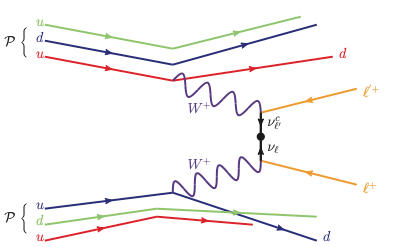
^{[Crédits: Phys. Rev. D103 (2021) 114014 (CC BY 4.0)]}

Les deux protons de gauche ‘émettent’ chacun un boson W. Ces boson interagissent ensuite pour produire deux leptons finaux par l’échange d’un neutrino intermédiaire. Dans l’exemple ci-dessus, les deux leptons ont la même charge électrique, qui est choisie positive. Une telle signature est très rare dans le Modèle Standard, de sorte que nous avons un signal très propre.

Ce processus ne mène à la production d’aucun neutrino final. Cependant, son étude permettra de tester les masses et mélanges des neutrinos par l’échange des neutrinos intermédiaires.

Dans notre publication, nous avons choisi comme exemple le cas où deux muons sont produits dans l’état final, car les muons sont des objets facilement identifiables dans un détecteur. Nous avons ainsi des conditions idéales pour tester l’idée et voir comment elle pourrait améliorer les connaissances actuelles.

Nous avons implémenté une analyse du signal permettant de contrôler le bruit de fond (les processus du Modèle Standard menant au même état final). En résultat, nous avons tout d’abord démontré que le signal pouvait être observé. On peut ensuite convertir les résultats en limites sur un paramètre m_𝝁𝝁 dans lequel mélanges et masses des neutrinos sont incorporés. Cela nous donne la figure ci-dessous pour différentes hypothèses de masse pour le neutrino le plus léger (l’axe des x).

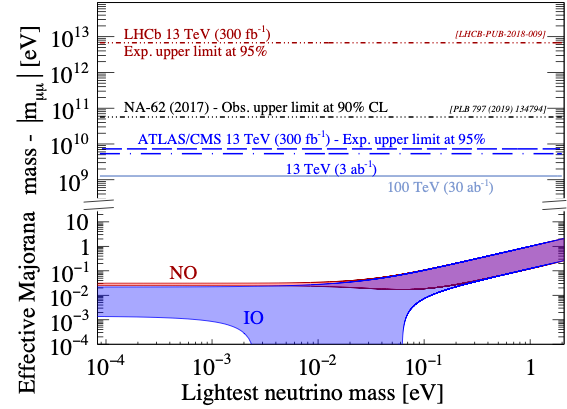
^{[Crédits: Phys. Rev. D103 (2021) 114014 (CC BY 4.0)]}

Les contraintes actuelles sont données par la ligne noire en trait pointillé. Tout ce qui se trouve au-dessus de cette ligne est exclu par les données. Nos prédictions pour le LHC correspondent aux lignes bleues. Tout ce qui se trouve au-dessus de ces lignes sera exclu d’ici une ou deux décennies. Cela implique une amélioration d’un facteur 10.

Nous avons ensuite estimé la sensibilité d’un futur collisionneur de 100 kilomètres de long qui fonctionnera à une énergie égale à 7 fois l’énergie du LHC. Tout ce qui se trouve au-dessus de la ligne bleuâtre pâle peut être atteint, ce qui correspond à une amélioration d’un facteur 100 relativement aux contraintes actuelles.

Malheureusement, les prédictions des modèles de neutrinos (les régions colorées en bas) requièrent une amélioration d’un facteur supplémentaire de 10,000,000,000. Cependant, toute amélioration est bonne à prendre car il faut vérifier l’absence de signal à tout m_𝝁𝝁 supérieur à ce qui est prédit par les modèles. D’où l’utilité de notre travail !

---

Une nouvelle façon d’étudier les neutrinos au LHC ? Mais qui que quoi donc où ?

---

Si je voulais résumer en quelques mots ce dont j’ai parlé aujourd’hui, je dirais simplement : neutrinos et mes propres recherches dans cette thématique (voir les publications ici et là). Dans ce blog, j’ai tenté de détailler ce que nous avons fait et pourquoi c’était important.

Les neutrinos sont les particules les plus mystérieuses du Modèle Standard. Nous en avons trois : le neutrino électronique, muonique et tau. Les neutrinos se mélangent cependant, de sorte que chaque neutrino a un petit bout de neutrino électronique, un petit bout de neutrino muonique et un petit bout de neutrino tau. Ce mélange requiert que les neutrinos soient massifs, et il ressort à nos expériences à mesurer masses et paramètres de mélange. C’est ici que mon travail intervient.

Nous avons proposé d’utiliser des processus sans neutrino pour tester les neutrinos au LHC et aux collisionneurs futurs. Dans ces processus, deux bosons W sont émis par les protons qui se collisionnent. Ces bosons W interagissent ensuite pour produire deux leptons de même charge électrique (deux électrons, deux positrons, deux anti-muons, un muon et un électron, etc.) via l’échange d’un neutrino intermédiaire. Une telle réaction est associée avec un faible bruit de fond du Modèle Standard, de sorte qu’elle offre une sonde propre de la physique des neutrinos et de la physique au-delà du Modèle Standard en général.

Dans nos deux articles, mes collaborateurs et moi-même avons démontré que les limites sur les paramètres des neutrinos pourraient être améliorées de façon significative aux collisionneurs présents (le LHC au CERN) et futurs (le FCC au CERN ou SPPC en Chine, si approuvées). Nous avons déterminé un facteur 100 d’amélioration en considérant un signal où deux muons sont produits.

Il reste à présent qu’à attendre le vrai test dans les données du LHC, dont les résultats devraient apparaître prochainement.

Et voilà ! Je pense que cela suffit pour aujourd’hui. J’espère que vous avez apprécié cette petite fenêtre sur mon travail de recherche. Comme d’habitude, questions, feedbacks et commentaires sont les bienvenus !

Rendez-vous la semaine prochaine pour un nouvel épisode. J’hésite à parler d’un projet de science participative à construire sur Hive et STEMsocial. Au final je parlerai peut-être d’autre chose… on verra. Bonne fin de semaine à tous et toutes !