Probability Of A Full House In Five Card Hand From 52 Card Deck
Probability Of A Full House In Five Card Hand From 52 Card Deck
Hi there. This is a short probability post. I don't get into much probability these days as I prefer the data analytics side of things. From time to time I do tutor and have to teach some probability stuff.
This post does feature a bit of classic problem. From a five card hand from a deck of 52 cards, what is the probability of a getting a full house? A full house is a three of a kind (triple) and a two a kind (double or pair).
Math text in image form is formed with LaTeX and QuickLaTeX.com.

Choose Notation & Combinations
In everyday life the word combination refers to a specific arrangement of items or numbers. As an example, the combination to a lock is 871. The order does matter here. Having 817, 178, 187, 781, and 718 uses the same numbers of 8, 7 and 1 but have a different order. In the probability framework that lock combination example is technically called a permutation as the order matters.
Combinations in probability does not consider order. When it comes to cards having something Ace, King is the same as King, Ace. A triple and a double is the same as a double and a triple when referred to a combination.
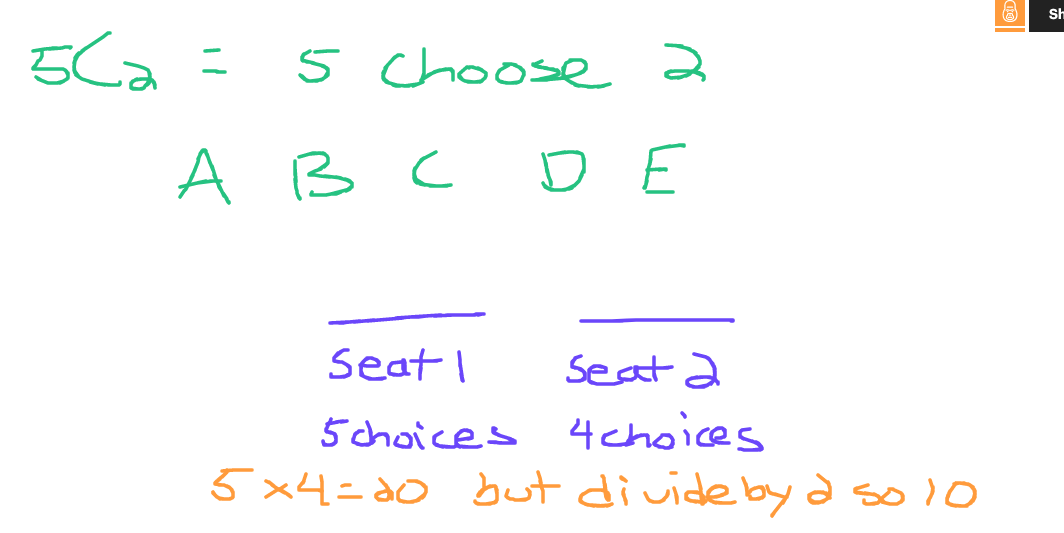
The concept of choose in probability refers to the idea of selecting a certain number of objects (denoted as n) into a number of positions, spots or spaces (denoted as k). If there are 5 people and 2 seats available there would be 5C2 (5 choose 2) = 10 ways of seating 5 people into 2 seats. The screenshot hand drawn from my tablet shows the thought process of 5 Choose two. Screenshot saved with Snipping Tool along with the website witeboard.com.
There are 5 people that can be selected for seat 1. Then there are four people that can be selected for seat 2. We divide by two (two factorial to be more precise) as order does not matter here. Getting seat 1 or seat 2 is counted the same as getting just a seat. Apologies if this is still confusing. You can view this video by Khan Academy for more details.

The Answer/Formula For Full House
A full house requires a triple and a double. You can get a triple first then a double or the other way around in the form of a double and a triple.
When you draw 5 cards from a deck of 52 cards there are 52 choose 5 five card hands. The number of five card hands is 2 598 960. This is the denominator for the answer.
The numerator is a bit more tricky. There are 13 values in a standard deck of cards. These are Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen and King. Each of the 13 values have 4 copies in the form of one heart, one club, one diamond and one spade.
For a triple I select one card value from the 13 and I choose three of them from the four. This product is:
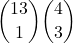
Dealing with a double is similar. Note that there would be 12 values to choose from as the triple is completed. It would be the following.
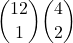
Combining these two products would give the numerator for the answer. The probability of a full house in 5 cards from a 52 card deck with no replacement is the following.
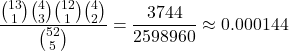
Double Then Triple In Full House Case
You could also do a double then a triple to get a full house. It may not seem like it but the numerator stills multiplies to 3744. The denominator is still the same at 2598960.
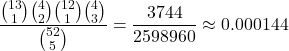

Posted using STEMGeeks
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.