Function Notation In Math

5 months ago

Hi there. Here is a guide on function notation in mathematics. This concept kind of has applications but this concept is a part of the algebra toolbox for math students.

Some math images rendered with Quicklatex.com.

Image Source

Topics

Why f(x) Notation Instead of y =
Substituting Number Values For x With Function Notation
Advanced Examples
Adding & Subtracting Functions

Why f(x) Notation Instead of y =

Suppose you have two equations that have y = to something. Let's say you have y = x + 2 and y = 3x + 10. If you have to substitute x = 1 into y, which y equation do you choose? The first one or the second one?

This is where function notation and f(x) comes in. We can rewrite the above equations as f(x) = x + 2 and g(x) = 3x + 10. Instead of saying substitute x = 1 into the function f(x) we can say obtain the value of f(1) (pronounced f of 1).

Function notation is a compact and simplified way of substituting values of x in different equations and functions.

Substituting Number Values For x With Function Notation

Let's take at some example of function notation with substituting numbers for x.

Example One

Let f(x) = 5x - 7, what is the value of f(10)?

Replace the variable x with the number 10. Then apply order of operations to get the answer of 43 (50 - 7).

Example Two

What is the value of g(-2) if g(x) = x^2 - 7?

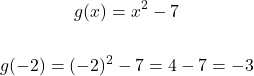
Example Three - Exponential Function

Evaluate h(3) if h(x) is ten to the power of x.

Image Source

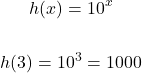
Advanced Examples

The idea of function notation is not super complicated but some examples can get a bit technical and algebra intensive. Here are a few tougher examples.

Example One

In f(x) = 5x + 2, what is f(2x)?

At first this looks confusing. What you have to do is replace the input x with the new input of 2x.

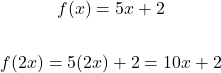
Example Two

In g(x) = 2x - 1, what is g(x + 7)?

Replace x with the new input of x + 7. Afterwards use algebra techniques to expand and simplify.

Image Source

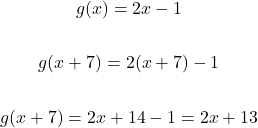
Adding & Subtracting Functions

This concept of adding and subtracting fractions is a natural extension of function notation. I could write another post dedicated to this but I have decided to put some stuff here.

You can combine adding & subtracting functions with evaluating them given a value of x.

Example One

If f(x) = x - 7, what is the value of f(1) - f(3)?

The value of f(1) is negative 6 and the value of f(3) is negative 4. When you compute f(1) - f(3) it is -6 - -4. The answer here is negative two.

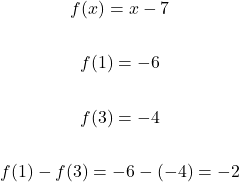
Example Two

With f(x) = 2x + 1 and g(x) = x - 3, what is the value of f(1) + g(3)?

From the function f(x) the value of f(1) is 3. The value of g(3) is 3 minus 3 which is equal to 0. Adding the values of f(1) and g(3) is 3 plus 0 which gives the answer of 0.