A Checkerboard Problem With Pascal's Triangle

Hi there. I have a somewhat interesting math problem that I encountered while tutoring. It was a checkerboard problem that included Pascal's Triangle.

 

Pascal's Triangle Review

---

Pascal's Triangle is an interesting triangle that contains symmetry and recursion. The top of the triangle begins with one. The second row is 1 and 1. In the third row the first term on the left is one, the second term that is below and in the middle of the two ones above is two. This number of two is from one plus one from above. The third and final term in the third row is 1.

Picture from this site

 

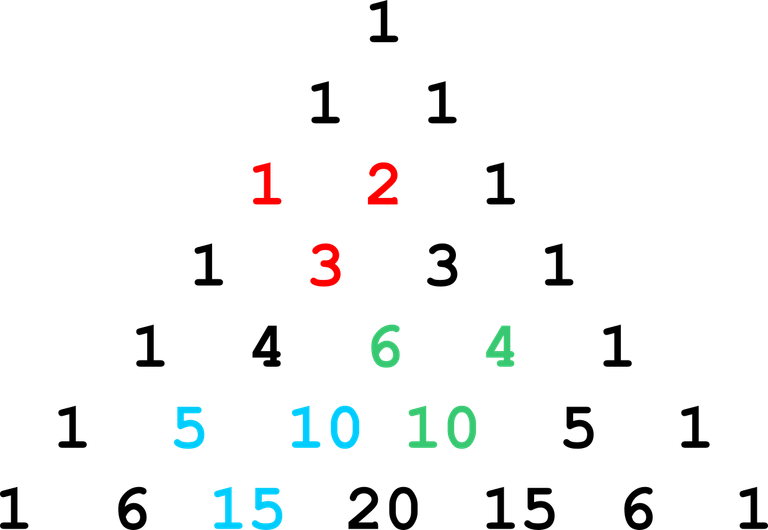
Ones appear at the start of each row and at the end of each row. You can compute the next number in the row by adding the two numbers that are diagonally above the spot. For example the number four from the fourth row from above is from the one that is above and to the left of four plus the three that is above and to the right of four.

 

Checkerboard Problem

---

Here is the scenario for the checkerboard problem.

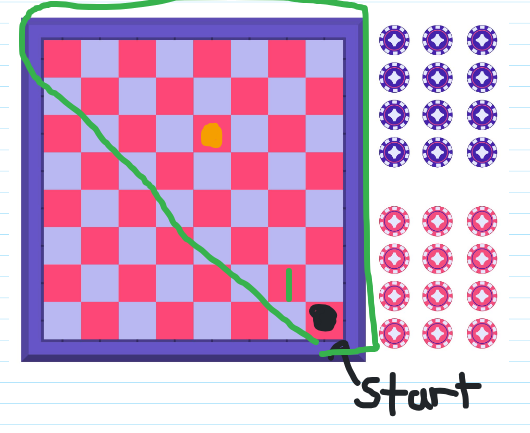
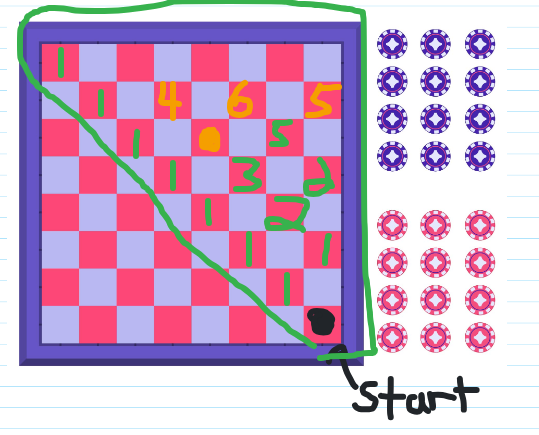
• Starting black piece is at the bottom right of the board.
• You can only move up and diagonally. Never downwards.
• There is a second piece (in orange in solutions) that takes up the space on the third row from the top and 5 spaces from the left.
• You cannot land on the same space as this second piece but you can jump over it.

 

The question is how many ways can the black piece from the bottom right reach the top row?

I was almost able to solve this question with the student in my tutoring session. After the session I took a look at this again and then I was able to solve it.

 

Solution

Screenshot images are from the closed end whiteboard website I tutor with.

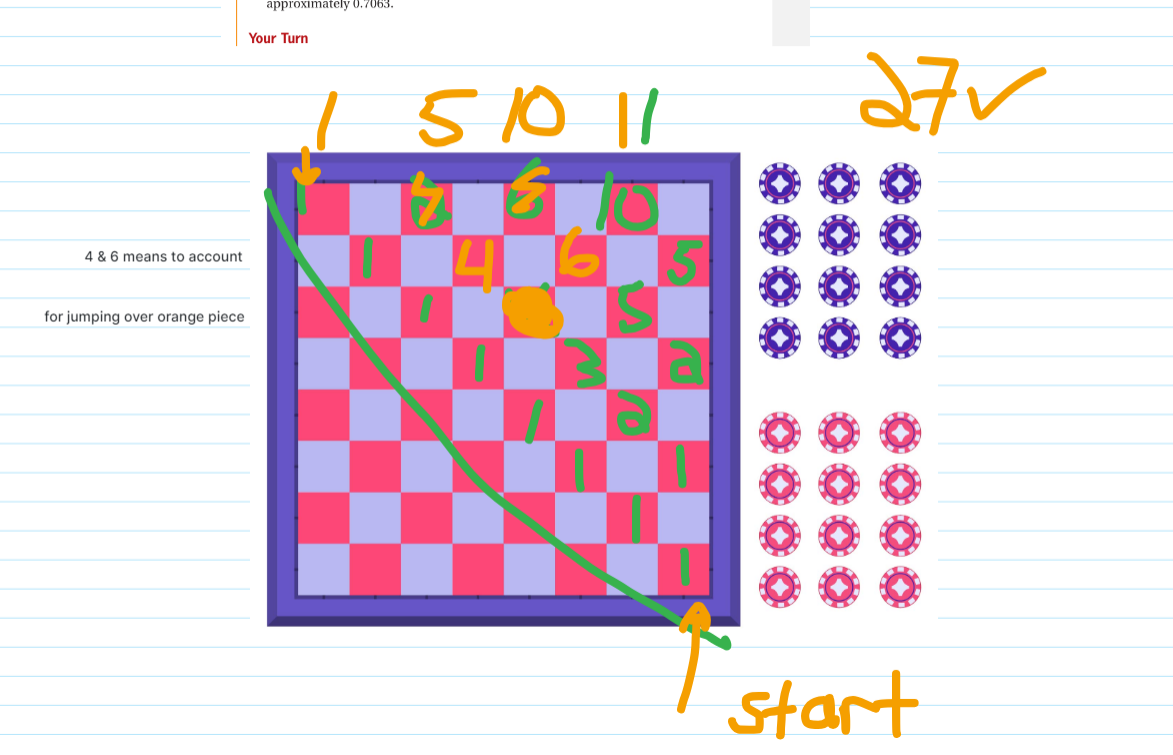
From the bottom right space the piece can only move up and to the left. That is one way which is labelled a one in the second last row from the top and the seventh column from the left.

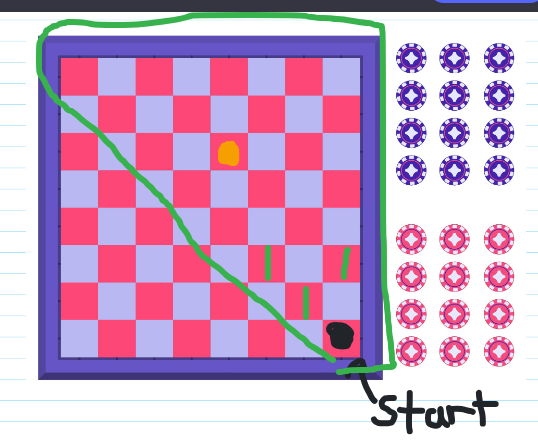
In the next step I can move either up and to the left or to the right. In both spaces there is only one way to get there each. I label ones there.

If I keep going up and to the left there is only one way to get there. Those are all labelled ones even at the top left corner. These ones along the main diagonal is similar to Pascal's triangle.

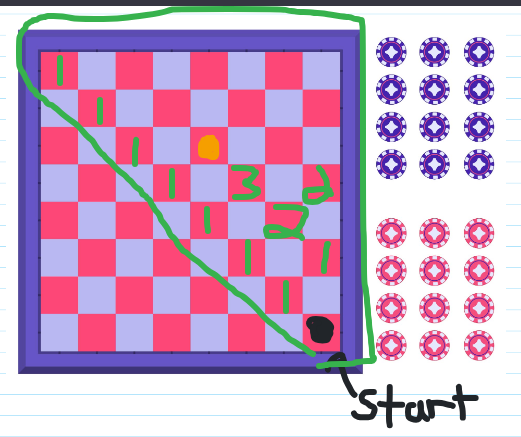
We can enter numbers on each square similar to Pascal's Triangle. The two in row 5, column 7 is from the two ones (1 plus 1) diagonally below it. The row that has 1, 3, 2 is from the 1 on the main diagonal of red squares, the three from 1 plus 2 and the two on the right side.

The third row with the second piece in orange can be tricky to work with. You cannot land on that same space but you can jump over it. The five is from three plus two. The four that is diagonally above the orange piece on the left is from the one in the third row and the three diagonally below the orange piece on the right. Six is from the five in the third row plus the one from the left side in the fourth tow.

Complete this Pascal triangle like pattern to obtain the number of ways of reaching the red squares at the top row. These numbers are 1, 5, 10 and 11. The sum of these numbers add up to the answer of 27.

This type of problem is not something I deal with often but with pattern recognition you can find a way to solve this. I do admit that I ask for the number solution from the student before finding the strategy behind the solution.

 

Thank you for reading.

Posted using STEMGeeks