Ejercicio Pendiente en el Post Anterior /// Exercise Pending in Previous Post

En el post anterior, quedo un ejercicio pendiente, el cual vamos a desarrollar hoy.

In the previous post, there was a pending exercise, which we are going to develop today.

---

Se trata del siguiente: /// It is the following:

---

Usando el Teorema del Valor Medio, verifique que:///Using the Mean Value Theorem, verify that:

---

---

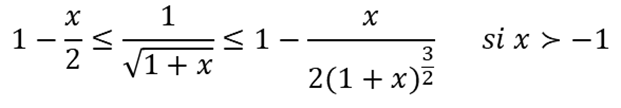
Comencemos por analizar que 𝑥<−1 , esto significa que x toma valores cercanos a -1 por la derecha, pero sin llegar a ser -1, en este caso la gráfica de la función es asintótica a la recta x= -1. De esta forma vemos que el límite inferior a del intervalo (a, b) con el cual vamos a trabajar es cercano a x= -1.

Let's start by analyzing that 𝑥<-1 , this means that x takes values close to -1 on the right, but without becoming -1, in this case the graph of the function is asymptotic to the straight line x= -1. Thus we see that the lower limit a of the interval (a, b) with which we are going to work is close to x= -1.

---

Sumemos a cada término de esa desigualdad, la expresión: /// Let us add to each term of this inequality, the expression:

---

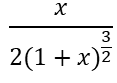
En este proceso, la desigualdad no va quedando así: /// In this process, inequality does not stay that way:

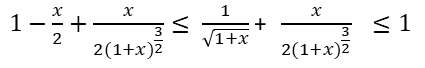
Restando 1 a cada miembro de la desigualdad, no queda así: /// Subtracting 1 from each member of the inequality, it does not look like this:

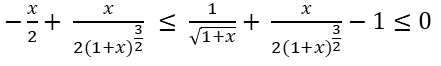
De este resultado podemos identificar:///From this result we can identify:

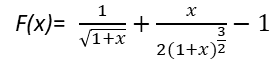
También identificamos b=0, como el límite superior del intervalo (a, b) donde queremos verificar las condiciones del Teorema del Valor Medio.

We also identify b=0, as the upper limit of the interval (a, b) where we want to verify the conditions of the Mean Value Theorem.

---

Al evaluar nuestra función en b=0, nos resulta que: ///Evaluating our function at b=0, we find that:

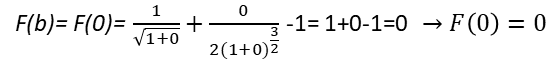
Con la ayuda de la calculadora gráfica Desmos, tracemos el gráfico de F/// With the help of the Desmos graphing calculator, let's plot the graph of F

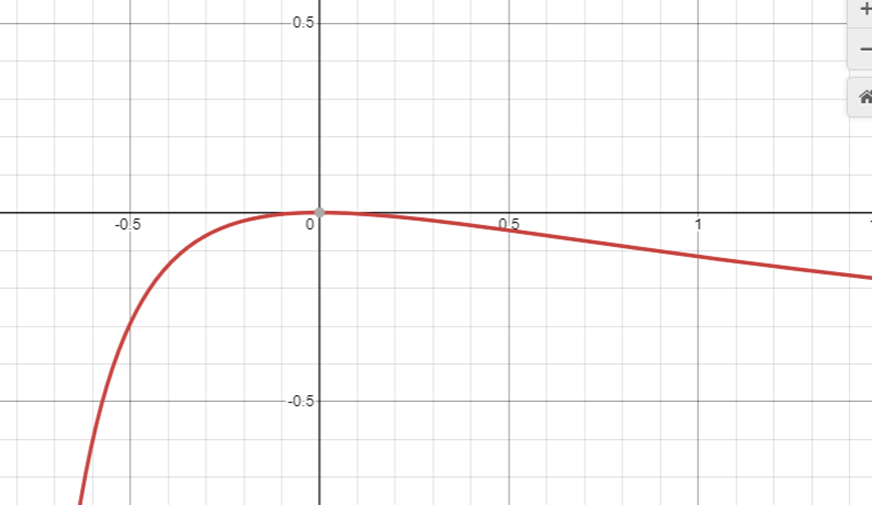
Tomemos un valor para a que se encuentre a la derecha de -1 y a la izquierda de 0, por ejemplo x=-0.5

---

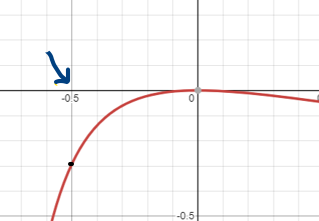
De acuerdo a la gráfica, F es una función continua en el intervalo (-0.5, 0) y diferenciable en el intervalo [0.5,0].

According to the graph, F is a continuous function in the interval (-0.5, 0) and differentiable in the interval [0.5,0].

---

Veamos que x=- 0.5 satisface la desigualdad dada./// Let us see that x=- 0.5 satisfies the given inequality.

---

Es decir, verifiquemos que:///That is, let us verify that:

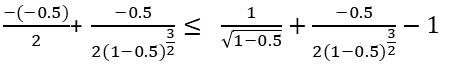
En efecto:///Indeed:

Al realizar las operaciones correspondientes, nos va quedando así:/// By performing the corresponding operations, we are left with the following result:

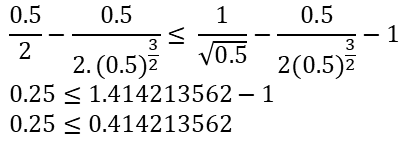
Con lo cual validamos que se cumple la desigualdad./// Thus we validate that the inequality is satisfied.

---

Calculemos F(-0.5)///Calculate F(-0.5)

---

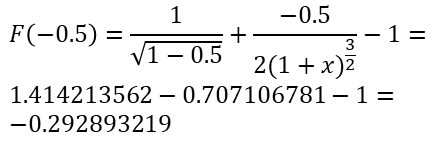
Luego/// Then

𝐹(-0.5) =−0.292893219

---

Nos falta calcular la derivada de F/// We need to calculate the derivative of F

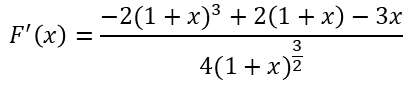
Apliquemos ahora el Teorema del Valor Medio/// Let us now apply the Mean Value Theorem

---

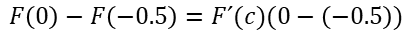
Resolviendo las operaciones correspondientes y sustituyendo valores, nos va quedando así:/// Solving the corresponding operations and substituting values, we are left with the following:

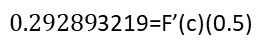
Despejando la derivada de F aplicada a c, nos queda:/// By subtracting the derivative of F applied to c, we are left with:

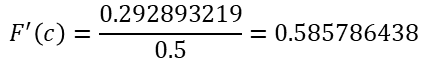
Sustituyendo x por c en la derivada de F, nos queda por resolver esta ecuación para c:

---

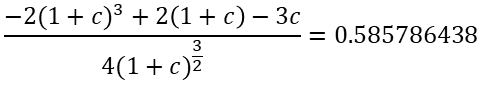
Solucionando la ecuación, el valor de c es aproximadamente -0,26577....

Con lo cual queda resuelto el problema planteado.

Solving the equation, the value of c is approximately -0,26577....
Thus, the problem is solved.

---

Créditos

El post es totalmente original de la autora.
Algunos conceptos se desarrollaron con el apoyo de los Textos:
‘'Cálculo Diferencial para Administración y Economía’'. Autor es Jorge Sáenz. Segunda Edición. Editorial Hipotenusa. Barquisimeto-Venezuela. 2007.
"Calculo Diferencial e Integral". Autores: Howard E. Taylor y Thomas L. Wade. Editorial Limusa. Mexico. 1974.
Para la gráfica nos apoyamos en la Calculadora Gráfica Desmos y Paint.

Credits
The post is entirely original by the author.
Some concepts were developed with the support of the Texts:
''Differential Calculus for Management and Economics''. Author is Jorge Sáenz. Second Edition. Hipotenusa Publishing House. Barquisimeto-Venezuela. 2007.
"Differential and Integral Calculus". Authors: Howard E. Taylor and Thomas L. Wade. Editorial Limusa. Mexico. 1974.
For the graphing we used the Desmos Graphing Calculator and Paint.

Posted with STEMGeeks