Earth in Upheaval Revisited – Part 40

~ Part 1 ~

In the eighth chapter of Earth in Upheaval Immanuel Velikovsky explored several potential causes of the Ice Ages:

• Secular Pole Shift
• Continental Drift
• Secular Changes in the Earth’s Orbit
• Secular Changes in the Earth’s Obliquity
• Rotating Crust

The first four causes were all found wanting for one reason or another―generally speaking, they operated too slowly or over too small a range―and Velikovsky rejected each of them in turn. The fifth cause seemed more promising, but a mechanism that would allow the Earth’s crust to rotate en masse while still satisfying all the evidence was elusive:

Not only must the cause have been more powerful than the agents invoked, but it must have acted with great suddenness ... Sudden the agent must have been, and violent; recurrent it must have been, but at highly erratic intervals; and it must have been of titanic power. (Velikovsky 117)

In the seven sections of Chapter IX, Axis Shifted, Velikovsky develops a working hypothesis to finally explain the Ice Ages. The first of these sections, Earth in a Vise, is introductory in nature. It is the shortest section in the chapter.

A power sufficient to dislodge the outermost layer of the planet must be sought outside the Earth itself:

The displacement of the shell alone requires forces not in existence on the earth itself; and the turning of the earth’s axis in a new direction requires more powerful forces still. (Velikovsky 118)

Left to its own devices, the Earth can only alter its obliquity―the tilt of its axis―by infinitesimal amounts spread over aeons of time. Currently, the obliquity is decreasing by less than 50 arcseconds per century. To alter the Earth’s obliquity suddenly and by an amount sufficient to account for the onset of an Ice Age we require an outside agent of titanic dimensions.

Harold Jeffreys

Harold Jeffreys

But do we even know that the obliquity has shifted significantly within the recent geological past? Velikovsky believes that we do, and he summons the British geophysicist Harold Jeffreys as his principal witness:

Harold Jeffreys asks in his book The Earth: “Has the inclination of the earth’s axis to the plane of its orbit varied during its history?” and proceeds: “The answer to [this] question is a definite ‘Yes!’ The theory of tidal friction … assumes the equator and the plane of the earth’s and moon’s orbits to coincide. The fact [is] that they do not. ...”

The moon, it is assumed, issued from the equatorial region of the earth by the process of disruption and must, therefore, revolve in the plane of the terrestrial equator; but since it does not, there must have been a displacement either of the moon or of the terrestrial axis; and the position of the moon close to the plane of the ecliptic suggests that the terrestrial axis suffered displacement. Also, if from the beginning there was a difference in the direction of the axes of terrestrial rotation and lunar revolution, this difference must have disappeared as the result of tidal friction. Jeffreys considered the works of George Darwin, who tried to explain the observed positions by recourse to several additional tidal frictions, but he found a flaw in Darwin’s hypothesis.

Any internal changes in the earth would be “not important” for the observed change in the direction of the terrestrial axis. Jeffreys says: “If we consider the axis of the earth’s angular momentum, this can change in direction only through couples acting on the earth from outside.” (Velikovsky 118–119 : Jeffreys 303)

Orbital Inclination of the Moon

Harold Jeffreys makes for a strange prop on which to build a theory of catastrophism. Read in context, his comments do not at all support the catastrophist slant Velikovsky has given them. Here is the entire section of The Earth from which Velikovsky lifted his quotation:

15·8. The Permanence of the Continents. Three questions are really involved under this head, and require separate treatment. Has the inclination of the earth’s axis to the plane of its orbit varied during its history? Have the poles always been the same points of the outer surface? Has the outer surface itself undergone considerable distortion, other than the recognized displacements involved in mountain formation and other geological processes?

15·81. The answer to the first question is definitely ‘Yes.’ The theory of tidal friction expounded in Chapter XIV is a simplified one, and assumes the equator and the planes of the earth’s and moon’s orbits to coincide. The fact that they do not introduces several additional tides depending on the inclinations and eccentricities of the orbits, and all these are affected by friction. The investigation of their effects formed the subject matter of most of the second volume of Darwin’s Scientific Papers, and he was able to show how they could have brought the system to its present state from an initial one with the earth and moon close together, the moon’s orbit nearly circular, and in the plane of the equator, and the equator at any rate much less inclined to that of the ecliptic than it is now. But he was using the hypothesis that the tidal friction is bodily, and it is not yet known how far his results would be altered if dissipation in strong tidal currents in shallow seas is the dominating type. Even the direction of the changes is somewhat in doubt, though the problem is probably capable of a definite solution.

In any case the effects of tidal friction on the inclinations must be slow and have acted in the same direction through most of the time concerned. In addition there are various periodic effects arising from astronomical causes, but all of these are small and have short periods, judged by geological standards. A further influence arises from internal changes in the earth, but is not important. If we consider the axis of the earth’s angular momentum, this can change in direction only through couples acting on the earth from outside. Apart from the tidal effect, the only couples concerned are due to the attractions of the sun and moon on the equatorial protuberance. Their main effect is the precession of the equinoxes, a motion of the axis of spin in a circular cone about the pole of the ecliptic; the associated changes in the inclination are small and have short periods. The inclination of the axis of the earth’s angular momentum to the plane of the orbit can have changed appreciably only through tidal friction. Further, the difference between the axis of angular momentum and the axis of rotation is very small, depending only on the actual angular momentum of the horizontal movements in progress at any time, and on the variation of latitude.

Fission Theory: Darwin’s Model of the Moon’s Formation

15·82. The other two questions do not concern the movement of the Earth as a whole, but only the displacements of parts of it relative to one another. They depend on a discussion of what forces exist and what displacements they are capable of producing. The chief of these deforming forces are the equatorial attraction, tidal friction, the attraction between continents, and perhaps an internal stress incidental to the precession of the equinoxes. The magnitude of the first is, we have seen, of order 4000 dynes/cm². Tidal currents at their strongest give a bottom drag of the order of 40 dynes/cm²; but this is abnormal and is reversed in direction in every tide where it does occur. The mean secular tidal friction producing the slowing down of the earth’s rotation corresponds to a westward stress of the order of only 10^–4 dynes/cm² over the earth’s surface. The attraction between continents may, we have seen, give stresses of the order of 10^–2 dynes/cm². The stress in precession that makes the whole of the earth precess at the same rate, instead of different shells precessing at different rates, is at most of order 60 dynes/cm², and this must be mainly alternating in direction. The chief of these factors is definitely the equatorial attraction. Now a horizontal stress of 4000 dynes/cm² over a circular continent of radius 2000 km would give a total force of 4000π (2 x 10⁸)² dynes. This is resisted by the strength of the lithosphere, say 40 km thick. An average stress of 10⁶ dynes/cm² around a cylinder of radius 2000 km through the lithosphere would suffice to prevent all movement. The strength at the surface is of order 10⁹ dynes/cm², and the support of the great mountains seems to point to greater strengths lower down. There is therefore not the slightest reason to believe that bodily displacements of continents through the lithosphere are possible.

Even the strength of the order of 10⁷ dynes/cm² inferred for the asthenosphere, on several grounds, would be enough to prevent permanent distortion by forces of the magnitude suggested; and it may be well to recall the evidence of the moon’s ellipticity that this strength is applicable to stresses lasting for intervals of the order of the whole age of the earth.

To adopt the view that the earth’s crust has no strength under stresses of long duration, in spite of the absence of theoretical justification for such a view and the definite evidence against it, makes it possible to account for some continental displacement, but not much. In this case the deforming stresses produce motion, resisted by the viscosity of the material undergoing deformation. We have seen that an ordinary viscosity (p) of 3 x 10²² c.g.s. is a lower limit to the viscosity of the intermediate layer under the stresses due to the weight of mountains. Under smaller stresses the viscosity may be higher. With this viscosity and a shearing stress of 10⁶ dynes/cm² the rate of shear would be 3 x 10^–18/sec., and notable distortion would be produced in 3 x 10¹⁷ sec. or 10¹⁰ years. But in the upper layer the viscosity is certainly much higher. The estimate just used is such as to permit a mountain chain to be flattened in 10⁷ years. The actual time is perhaps 30 times as long. Further, the estimate refers to the intermediate layer; if the granitic layer had a similar viscosity the old mountain ranges would not be still standing. Thus the actual time needed to distort the outer crust is much more than 10¹⁰ years, and a large multiple of the time available. The question concerning the possibility of considerable distortion of the outer crust during geological time must therefore be answered in the negative.

15·83. Displacements of the outer crust bodily over the interior would involve no distortion of the outer crust except the small up and down ones rendered necessary by the ellipticity of figure. The elasticity and viscosity of the lithosphere would not resist this process. Now the variation of latitude shows that the viscosity of the rocky shell in general exceeds 5 x 10²⁰ c.g.s. A shearing stress of 4000 dynes/cm² over the surface would produce shear at a rate 0·8 x 10^–17/sec., and the crust would be displaced through a radian in a time of the order of 10¹⁷ sec. or 3000 million years. But this rate must be reduced to allow for the fact that this is the equatorial drift; the continents cannot move independently, but can only turn the crust as a whole so as to bring the greatest projections over the equator, so that the stress is resisted by the viscosity of the whole interior and not merely by the parts immediately under the main continents. It seems unlikely that this cause can have turned the crust by more than 5° during geological time.

15·84. The answers to our questions seem to be, therefore, as follows. A slow secular change of the inclination of the earth’s axis to the ecliptic during geological time is to be expected; the change has probably been on the whole an increase, but this is not quite certain. Secular drift of continents relative to the rest of the crust, such as have been maintained by A. Wegener and others, are out of the question. A small drift of the crust as a whole over the interior is not impossible; it would be shown as a displacement of the poles relative to the earth’s surface, but the maximum amount seems too small to be of much interest. (Jeffreys 303–305)

Giant Impact Hypothesis

We now know that Jeffreys was wrong when he ruled out the possibility of continental drift. This does not augur well for the value of his opinion concerning other geophysical processes. Nevertheless, he is clearly a gradualist, who had little time for sudden, large, and catastrophic changes taking place in the Earth’s crust. But Velikovsky is happy to cite this Uniformitarian to the effect that the axial tilt of the Earth has changed, leaving the door open for further argument:

The arguments of astronomers against the idea of the geologists concerning the change in the position of the terrestrial axis were correct only in showing that the terrestrial causes could not effectively displace the axis of the earth; but the very fact of displacement is now claimed because of astronomical considerations and by such an authority in this field as Jeffreys. What could have played the role of couples, or a vise, acting from outside? And, again, was it a gradual change or a sudden displacement? (Velikovsky 119)

Jeffreys was only prepared to concede a slow, secular change in the Earth’s obliquity due to the pull of the Moon and the Sun on the Earth’s equatorial bulge. According to current thinking, the axial tilt oscillates very slowly over a period of about 41,040 years and within a range of only a few degrees (approximately 22°–25°). Clearly, this is insufficient for Velikovsky’s purposes. But is it possible that current thinking is simply wrong?

The Lunar Inclination Problem

Jeffreys deduced that the obliquity must have changed over geological time because the Moon does not orbit the Earth in the Earth’s equatorial plane. The Moon’s orbit is tilted by about 5° to the Earth’s ecliptic―the plane of the Earth’s orbit around the Sun. This is much greater than it ought to be:

The Moon is generally thought to have formed from the debris ejected by the impact of a planet-sized object with the proto-Earth towards the end of planetary accretion ...

The Moon-forming impact is thought to have generated a compact circumplanetary disk (within < 10 Earth radii) from which the Moon rapidly accreted. Like Saturn’s rings, the proto-lunar disk is expected to become equatorial on a timescale rapid relative to its evolutionary timescale. Hence, so long as the proto-lunar material disaggregated into a disk following the giant impact, the Moon is expected to have accreted within ~1° of the Earth’s equator plane. Tidal evolution calculations suggest that for every degree of inclination of the lunar orbit plane relative to the Earth’s equator plane at an Earth-Moon (EM) separation of 10 Earth radii (RE), the current lunar orbit would exhibit ~½° of inclination relative to Earth’s orbital plane. The modern ~5° lunar inclination would―without external influences―translate to a ~10° inclination to Earth’s equator plane at 10 RE shortly after lunar accretion. This ~10x difference between theoretical expectations of lunar accretion and the EM system has become known as the lunar inclination problem. (Pahlevan & Morbidelli 492)

The only solutions astrophysicists have come up with for this problem involve speculative computer models. Pahlevan & Morbidelli explain the observed phenomena by assuming that in addition to giant impacts, such as the one that is believed to have created the Moon, there must have been innumerable smaller close calls. The cumulative effect of these collisionless encounters, they believe, can account for the current tilt of Moon’s orbit.

Ćuk and Stewart Solution

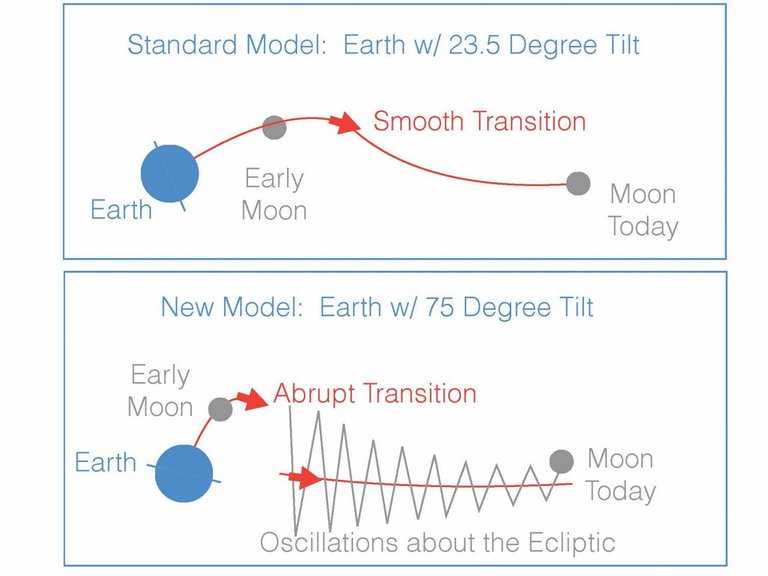
Another solution was proposed in 2012 by Matija Ćuk & Sarah Stewart of the University of California:

Here we show that tidal dissipation due to lunar obliquity was an important effect during the Moon’s tidal evolution, and the lunar inclination in the past must have been very large, defying theoretical explanations. We present a tidal evolution model starting with the Moon in an equatorial orbit around an initially fast-spinning, high-obliquity Earth, which is a probable outcome of giant impacts. Using numerical modelling, we show that the solar perturbations on the Moon’s orbit naturally induce a large lunar inclination and remove angular momentum from the Earth–Moon system. ―Ćuk et al 402

But these are just two of the many ways in which the Lunar Inclination Problem might be solved. The Moon’s anomalous orbital inclination could just as easily be due to a relatively recent close encounter. Of course, no gradualist is going to propose such a solution.

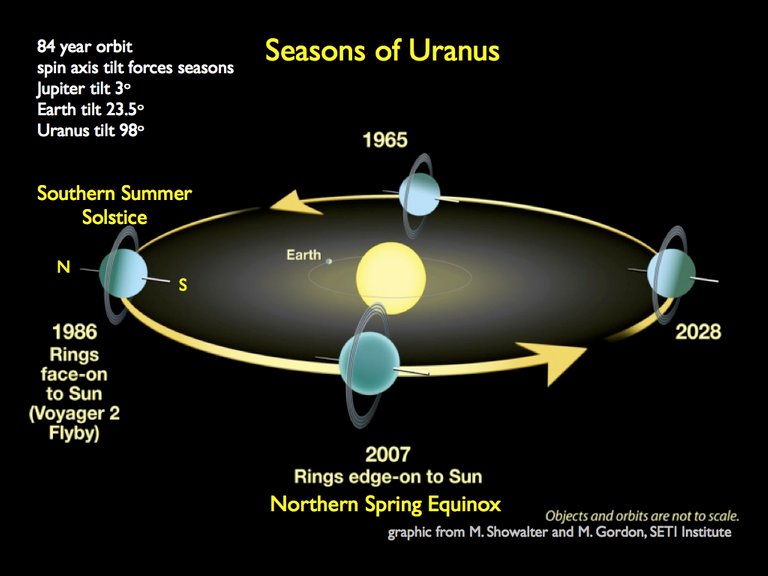
Uranus and Its Moons

A fine illustration of the phenomenon described by Pahlevan & Morbidelli is provided by the Uranian system. The planet Uranus has an axial tilt of 97.77°―the planet orbits the Sun on its side. It was once thought that the planet was knocked over by a giant impact during the early history of the Solar System. But today eighteen of the Uranian moons orbit the planet in its equatorial plane. The theory was that the debris from the impact coalesced to form the eighteen regular moons in the planet’s equatorial plane. Once again, this theory is based on computer simulations, and it is not the only explanation proposed to account for the unusual obliquity of Uranus. Recently less catastrophic models have been developed.

Uranus has nine other moons, but the orbits of these are not coplanar with the planet’s equator. It is thought that these moons were captured after the impact―or whatever it was that caused the planet to tip over.

But will Uranus’s equatorial bulge eventually pull these irregular satellites into the equatorial plane? And if it will, how long will that take? J M Danby considers this case in Chapter 11.15 of his Fundamentals of Celestial Mechanics. He has found that the orbit of a satellite revolving about an oblate planet will undergo what is called nodal precession, but the inclination, i, of its orbit will not be altered by the pull of the planet’s equatorial bulge:

11.15 The Motion of a Satellite in the Field of an Oblate Planet

... We see immediately from this that a [semi-major axis], e [eccentricity] and i [orbital inclination] suffer no secular perturbations ...

Hence for an oblate planet, the nodes regress. The line of apsides advances or regresses ... (Danby 260 ... 261 ... 261)

We cannot, then, conclude that the orbital inclination of the Moon―assuming the Moon once orbited in the Earth’s equatorial plane―must have been recently disturbed, arguing that if it had been disturbed long ago the attraction of the equatorial bulge would have pulled the satellite back into the equatorial plane by now. This does not mean that the Moon’s orbit has not changed catastrophically within the very recent past―as Velikovsky will argue. It simply means that we cannot use the Lunar Inclination Problem to prove that such changes must have taken place.

Uranus and Its Rings

And that’s a good place to stop.

---

References

• Matija Ćuk, Sarah Stewart, Douglas P Hamilton, Simon J Lock, Tidal Evolution of the Moon from a High-Obliquity, High-Angular-Momentum Earth, Nature, Volume 539, Pages 402–406, Springer Nature, London (2016)
• George Darwin, Scientific Papers, Volume 2, Tidal Friction and Cosmogony, Cambridge University Press, Cambridge (1908)
• Harold Jeffreys, The Earth: Its Origin, History and Physical Constitution, Second Edition, Cambridge University Press, Cambridge (1929)
• Kaveh Pahlevan & Alessandro Morbidelli, Collisionless Encounters and the Origin of the Lunar Inclination, Nature, Volume 527, Pages 492–494, Nature Portfolio, Springer, London (2015)
• Immanuel Velikovsky, Earth in Upheaval, Pocket Books, Simon & Schuster, New York (1955, 1977)

Image Credits

• Earth in Upheaval: First Edition, © Doubleday (1955), Fair Use
• Earth in a Vise: iStock, Getty Images, Fair Use
• Harold Jeffreys: © International Seismological Centre (photographers), Fair Use
• Orbital Inclination of the Moon: NASA, Visible Earth, Public Domain
• Fission Theory: Darwin’s Model of the Moon’s Formation: T E R Phillips & W H Steavenson, Hutchinson’s Splendour of the Heavens, Volume 1, Page 3, Hutchinson & Co, London (1923) : L E A (illustrators), Public Domain
• Giant Impact Hypothesis: © Citronade (illustrator), Creative Commons License
• Ćuk and Stewart Solution: © Douglas P Hamilton (illustrator), Fair Use
• Uranus and Its Rings: © M Showalter & M Gordon, SETI Institute, Fair Use