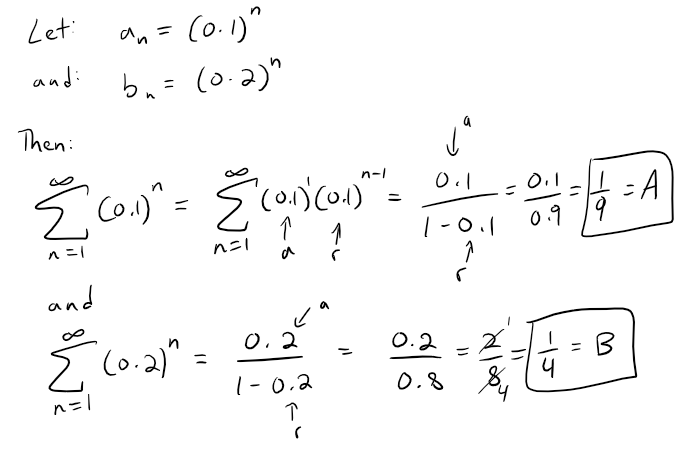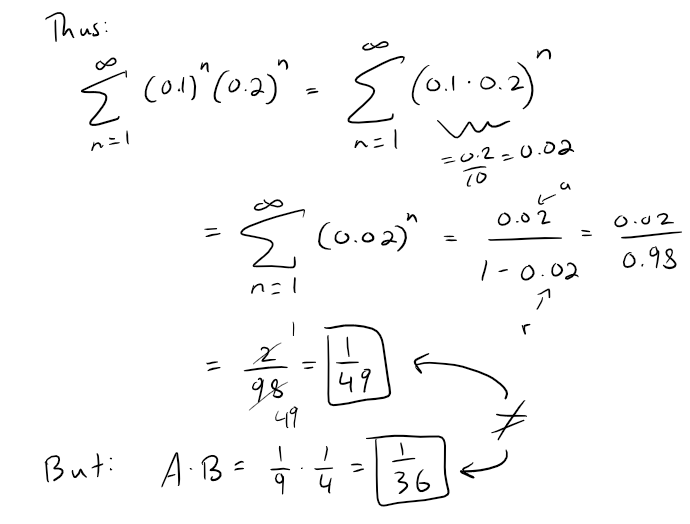Infinite Sequences and Series: Review and True-False Quiz
In this video I go over further into infinite sequences and series and this time go over the end-of-chapter Review and True-False quiz. These sections are at the end of most chapters of my calculus book, and are a great way to recap the concepts covered in each chapter. This video is a great review to challenge and help fine-tune your understanding of all things infinite sequences and series.
The topics covered in this video are listed below with their time stamps.
- 0:00 - Intro
- 1:23 - Calculus Book Reference
- 1:43 - Topics to Cover
- 2:39 - Review: Concept Check
- 2:43 - Question 1
- 8:10 - Question 2
- 11:40 - Question 3
- 17:17 - Question 4
- 18:39 - Question 5
- 29:16 - Question 6
- 31:01 - Question 7
- 49:58 - Question 8
- 59:21 - Question 9
- 1:08:53 - Question 10
- 1:15:52 - Question 11
- 1:25:22 - Question 12
- 1:29:54 - True - False Quiz
- 1:30:22 - Question 1
- 1:33:09 - Question 2
- 1:36:02 - Question 3
- 1:37:27 - Question 4
- 1:50:05 - Question 5
- 2:02:45 - Question 6
- 2:06:21 - Question 7
- 2:12:10 - Question 8
- 2:15:26 - Question 9
- 2:16:44 - Question 10
- 2:18:43 - Question 11
- 2:22:34 - Question 12
- 2:24:39 - Question 13
- 2:32:15 - Question 14
- 2:33:34 - Question 15
- 2:35:03 - Question 16
- 2:35:57 - Question 17
- 2:37:24 - Question 18
- 2:39:13 - Question 19
- 2:45:30 - Question 20
- 2:48:15 - Question 21
- 2:48:56 - Question 22
PDF video notes and sections playlist
- PDF video notes: https://1drv.ms/b/s!As32ynv0LoaIiY5Fc9tFyA7oQhImmw
- Video sections playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0FCqXVJv1r7eJvrvphfkr6L
- Full Vectors and the Geometry of Space series: https://www.youtube.com/playlist?list=PLai3U8-WIK0FjJpwnxwdrOR7L8Ul8VZoZ
Watch video on:
- 3Speak: https://3speak.tv/watch?v=mes/pdmqufgq
- BitChute: https://www.bitchute.com/video/EZxqvGQIZXdU/
- Odysee: https://odysee.com/@mes:8/Sequences-and-Series--Review-and-Quiz:8
- Rumble: https://rumble.com/v1q72lk-infinite-sequences-and-series-review-and-true-false-quiz.html
- DTube:
- YouTube: https://youtu.be/F0dsQLdXXpI
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
Follow my research in real-time on my MES Links Telegram: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truthReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Join my forums!
- Hive community: https://peakd.com/c/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android

Calculus Book Reference
Note that I mainly follow along the following calculus book.
- Calculus: Early Transcendentals 7th Edition by James Stewart
- Note: The previous videos I used the 6th edition.
Chapter Review and True-False Quiz
At the end of most chapters in my calculus book, there is a Review section and a True-False Quiz. Since it has been about a year since my last math video, I think it would be best to go over this review as a refresher on all things Infinite Sequences and Series.
Topics to Cover
- Review: Concept Check
- Question 1
- Question 2
- Question 3
- Question 4
- Question 5
- Question 6
- Question 7
- Question 8
- Question 9
- Question 10
- Question 11
- Question 12
- True - False Quiz
- Question 1
- Question 2
- Question 3
- Question 4
- Question 5
- Question 6
- Question 7
- Question 8
- Question 9
- Question 10
- Question 11
- Question 12
- Question 13
- Question 14
- Question 15
- Question 16
- Question 17
- Question 18
- Question 19
- Question 20
- Question 21
- Question 22
Review: Concept Check
Question 1
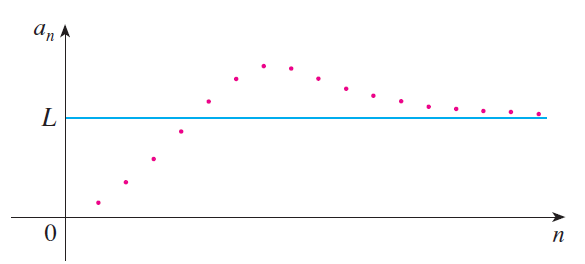
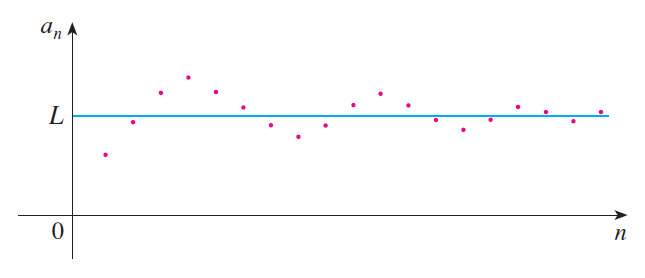
(a) What is a convergent sequence?
(b) What is a convergent series?
(c) What does limn→∞ an = 3 mean?
(d) What does ∑∞n=1 an = 3 mean?
Solution:
Part (a)
Recall from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-limits-squeeze-theorem-fibonacci-sequence-and-golden-ratio-more
Retrieved: 20 May 2022
Archive: https://archive.ph/PMR4G

The following graphs show sequences that converge to the limit L.
Part (b)
Recall from my earlier video:
https://peakd.com/mathematics/@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more
Retrieved: 20 May 2020
Archive: https://archive.ph/T5ZU5

Part (c)
The terms of the sequence {an} approach 3 as n becomes large.
Part (d)
By adding sufficiently many terms of the series, we can make the partial sums as close to 3 as we like.
Question 2
(a) What is a bounded sequence?
(b) What is a monotonic sequence?
(c) What can you say about a bounded monotonic sequence?
Solution:
Part (a)
Recall from my earlier video:

The graph below is an example of a sequence bounded above by M (or L) and bounded below by 0.
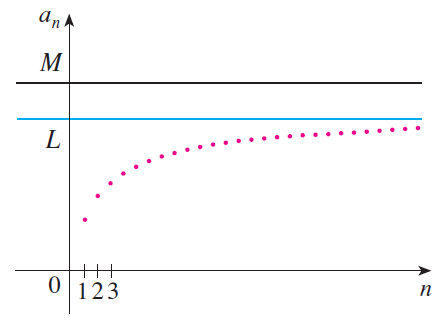
Part (b)
A sequence is monotonic if it is either increasing or decreasing, as per the same video above:

Part (c)
Recall from the same video above:

Question 3
(a) What is a geometric series?
- Under what circumstances is it convergent?
- What is its sum?
(b) What is a p-series?
- Under what circumstances is it convergent?
Solution:
Part (a)
Recall from my earlier video:


A geometric representation is shown below via similar triangles, where s is the sum of the series.
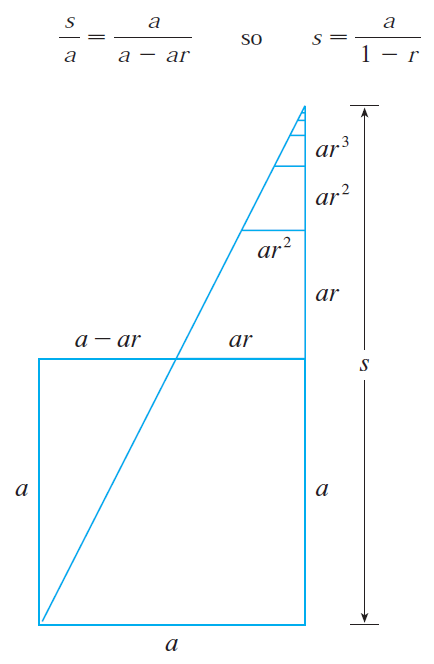
Part (b)
Recall from the same video referenced above:
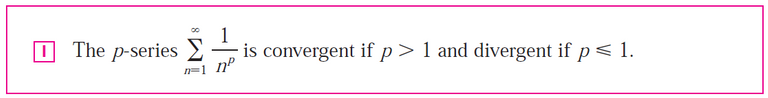
Question 4
Suppose ∑ an = 3 and sn is the n-th partial sum of the series.
What is limn→∞ an?
What is limn→∞ sn?
Solution:
If ∑ an = 3, then limn→∞ an = 0 and limn→∞ sn = 3.
Question 5
State the following.
(a) The Test for Divergence
(b) The Integral Test
(c) The Comparison Test
(d) The Limit Comparison Test
(e) The Alternating Series Test
(f) The Ratio Test
(g) The Root Test
Solution:
Part (a)
Recall from the same video above:

Part (b)
Recall from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-integral-test-and-estimate-of-sums
Retrieved: 20 May 2022
Archive: https://archive.ph/wip/I663M

Part (c)
Recall from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-comparison-tests
Retrieved: 20 May 2022
Archive: https://archive.ph/wip/78Zkq

Part (d)
Recall from the same video above:
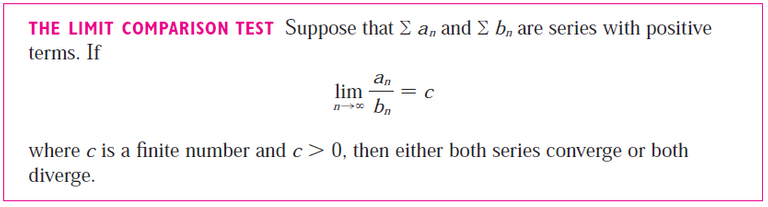
Part (e)
Recall from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-alternating-tests
Retrieved: 20 May 2022
Archive: https://archive.ph/vXXjE

This can be seen visually:
Part (f)
Recall from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests
Retrieved: 20 May 2022
Archive: https://archive.ph/wip/PtNst

Part (g)
Recall from the same video above:

Question 6
(a) What is an absolutely convergent series?
(b) What can you say about such a series?
(c) What is a conditionally convergent series?
Solution:
Part (a)
Recall from the same video above:

Part (b)
Recall also from the same video above:

Part (c)
Recall also from the same video above:

Question 7
(a) If a series is convergent by the Integral Test, how do you estimate its sum?
(b) If a series is convergent by the Comparison Test, how do you estimate its sum?
(c) If a series is convergent by the Alternating Series Test, how do you estimate its sum?
Solution:
Part (a)
We can use the steps and formula from my earlier video:

To estimate the sum, we first need to estimate the size of the remainder.
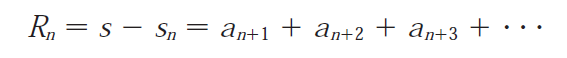
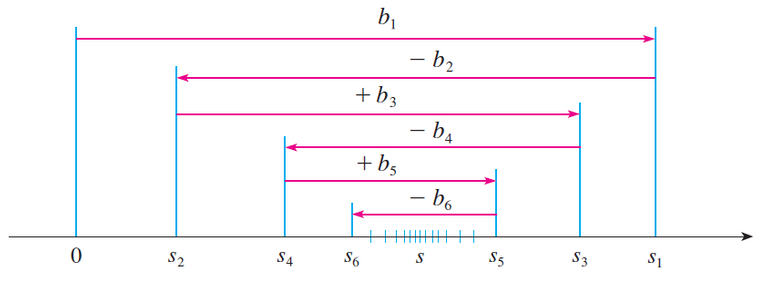
Note that the terms an+1, an+2, an+3, etc., are all the terms that remain, since s is the infinite convergent sum of terms, while sn is just the partial sum up to n terms.
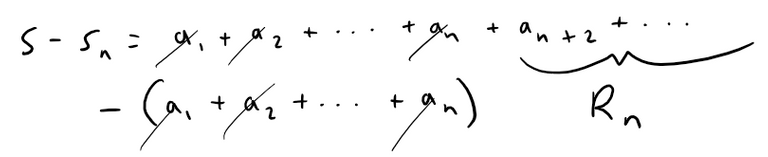
Depending on whether we integrate starting from n or n + 1 we can have an upper and a lower bound for the remainder.

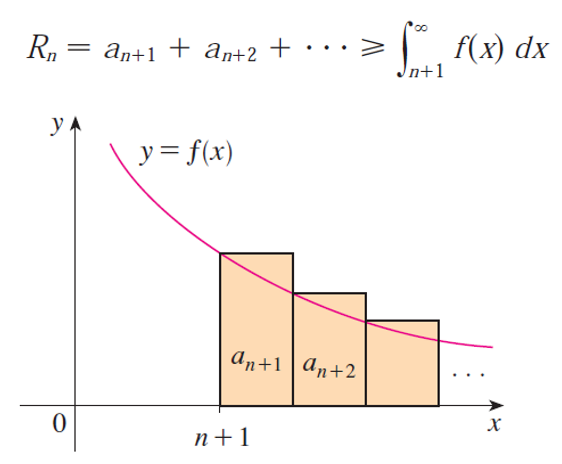
Thus the remainder is between two integrals.

Likewise, the sum can now be estimated as follows:
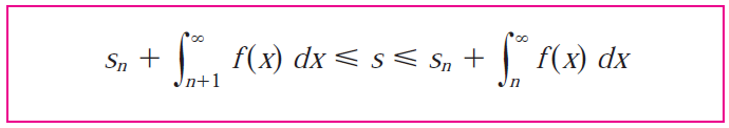
Part (b)
We can estimate the sum using the remainder estimate of the convergent series being compared, such as in the example from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-comparison-tests


Note that ∑ 1/n3 is a convergent p-series.
For reference, here is integral from the Example referenced above:

Part (c)
We can add terms until we reach a desired accuracy given by the Alternating Series Estimation Theorem, as stated in my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-alternating-tests

We can visualize this theorem from the earlier figure above:

Notice that s - s4 < b5, |s - s5| < b6, and so on.
Question 8
(a) Write the general form of a power series.
(b) What is the radius of convergence of a power series?
(c) What is the interval of convergence of a power series?
Solution:
Part (a)
Recall the general form of a power series from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-power-series
Retrieved: 21 May 2022
Archive: https://archive.ph/CGE8k
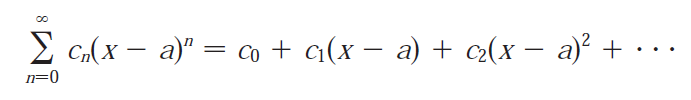
Part (b)
Recall the radius of convergence from the above video:

To summarise, the radius of convergence is:
(i) 0 if the series converges only when x = a.
(ii) ∞ if the series converges for all x.
(iii) a positive number R such that the series converges for |x - a| < R and diverges for the case |x - a| > R.
Part (c)
As stated above, the interval of convergence of a power series is the interval that consists of all values of x for which the series converges.
Corresponding to the cases in part (b), the interval of convergence is:
(i) the single point {a}.
(ii) all real numbers, that is, the real number line (-∞, ∞).
(iii) an interval with endpoints a - R and a + R which can contain neither, either, or both of the endpoints.
In case (iii) we must test the series for convergence at each endpoint to determine the interval of convergence.
Question 9
Suppose f(x) is the sum of a power series with radius of convergence R.
(a) How do you differentiate f?
- What is the radius of convergence of the series for f'?
(b) How do you integrate f?
- What is the radius of convergence of the series for ∫ f(x)dx?
Solution:
Parts (a) and (b)
Recall from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-representations-of-functions-as-power-series
Retrieved: 21 May 2022
Archive: https://archive.ph/wip/yCJp5


Question 10
(a) Write an expression for the n-th degree Taylor polynomial of f centered at a.
(b) Write an expression for the Taylor series of f centered at a.
(c) Write an expression for the Maclaurin series of f.
(d) How do you show that f(x) is equal to the sum of its Taylor series?
(e) State Taylor's Inequality.
Solution:
Part (a)
Recall from my earlier video.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-taylor-and-maclaurin-series
Retrieved: 21 May 2022
Archive: https://archive.ph/wip/QVFhu
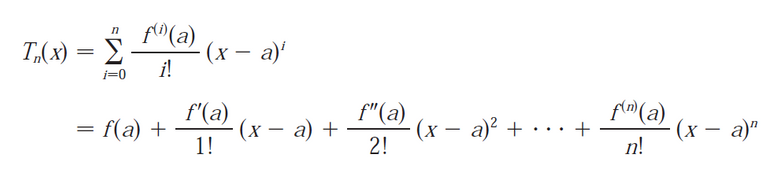
Part (b)
Recall from the same video above:
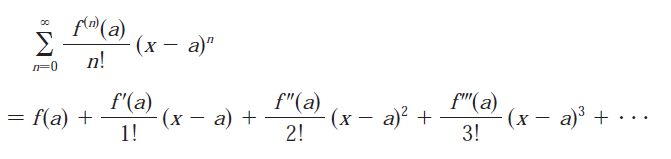
Part (c)
Recall from the same video above:
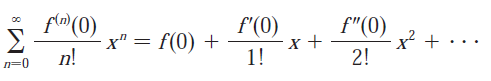
Note that the Maclaurin series is just the special case of the Taylor series where a = 0.
Part (d)
Recall from the same video above:

Part (e)
Recall from the same video above:
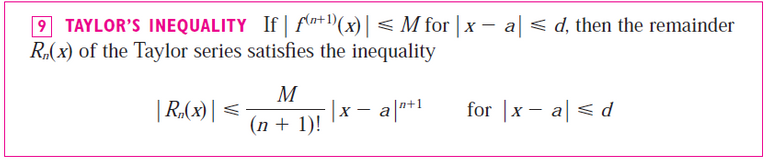
Question 11
Write the Maclaurin series and the interval of convergence for each of the following functions.
(a) 1 / (1 - x)
(b) ex
(c) sin x
(d) cos x
(e) tan-1(x)
(f) ln(1 + x)
Solution:
Parts (a) to (f)
Recall from the same video above:

Note that the above image includes the power series for ln(1 + x), which is from the 7th edition of my calculus book, while the 6th edition (which I used for my previous video) did not have it.
However, I went over ln(1 - x) in a later video: https://peakd.com/mathematics/@mes/infinite-sequences-and-series-representations-of-functions-as-power-series

Note that we can replace x with (-x) in the above ln(1 - x) power series to get the power series for ln(1 + x).
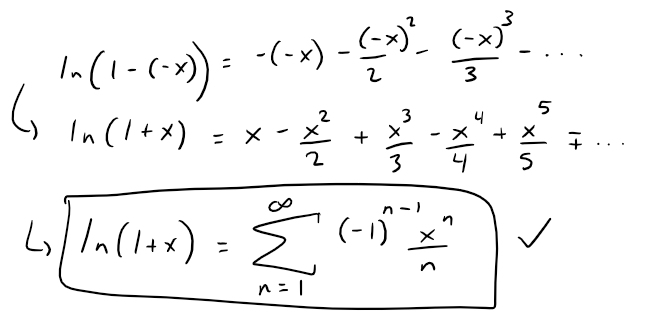
Question 12
Write the binomial series expansion of (1 + x)k.
What is the radius of convergence of this series?
Solution:
Recall from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-taylor-and-maclaurin-series
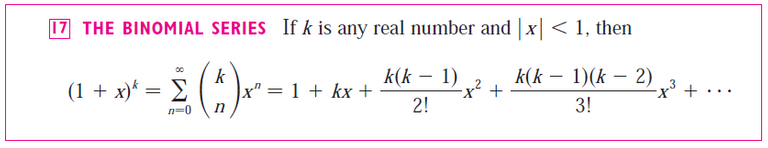
The radius of convergence for the binomial series is 1.
Note that the term in big brackets is the binomial coefficients and often pronounced as "k choose n".
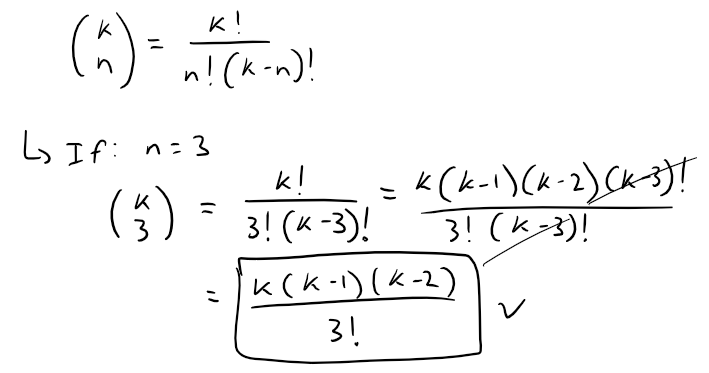
True - False Quiz
Determine whether the statement is true or false.
If it is true, explain why.
If it is false, explain why or give an example that disproves the statement.
Question 1
If limn→∞ an = 0, then ∑ an is convergent.
Solution: False
Recall from my earlier video:


Note also that the harmonic series ∑ 1/n is a divergent p-series.
Question 2
The series ∑∞n=1 n-sin 1 is convergent.
Solution: False
Note that this is just a p-series where p ≤ 1.
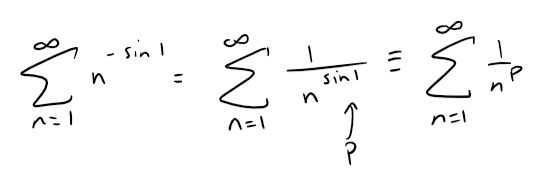
Calculation check:
sin(1) = 0.0174524064372835 (in degrees)
sin(1•180/pi) = 0.841470984807896 (in radians). Unless otherwise stated, this is usually the case.
Since p = sin 1 ≈ 0.84 ≤ 1, the p-series diverges.
Question 3
If limn→∞ an = L then limn→∞ a2n+1 = L.
Solution: True
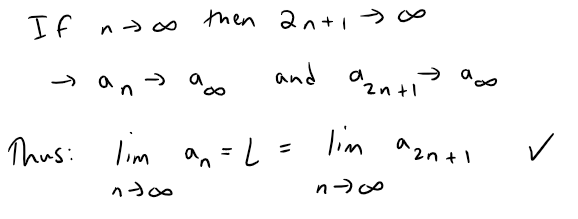
Question 4
If ∑ cn6n is convergent, then ∑ cn(-2)n is convergent.
Solution: True
Solution 1: Radius of Convergence Theorem
We can see this is this case by considering the radius of convergence theorem from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-power-series
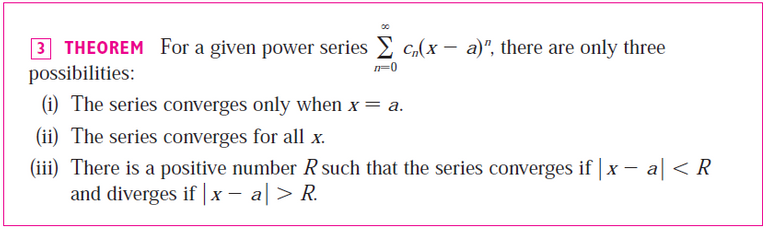
When x = a ± R, the series might converge or might diverge, that is, no information is known about the endpoints.
In our case, the series either converges according to (ii) or (iii).

We compare this to the other series:
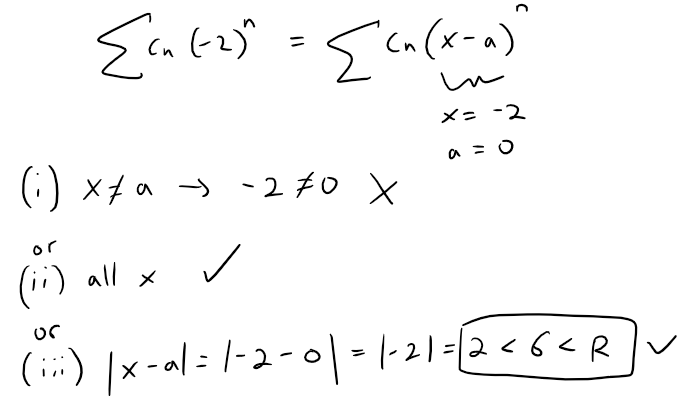
Thus if ∑ cn(6)n converges, then so does ∑ cn(-2)n also converges.
Solution 2: Comparison Test
We can also see that ∑ cn(-2)n converges by the comparison test.
First, recall the comparison test from my earlier video:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-comparison-tests

In our case, we can take the absolute value and show that ∑ cn(-2)n converges absolutely:
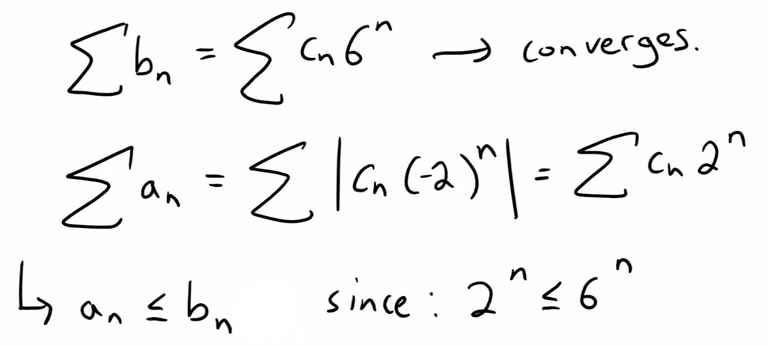
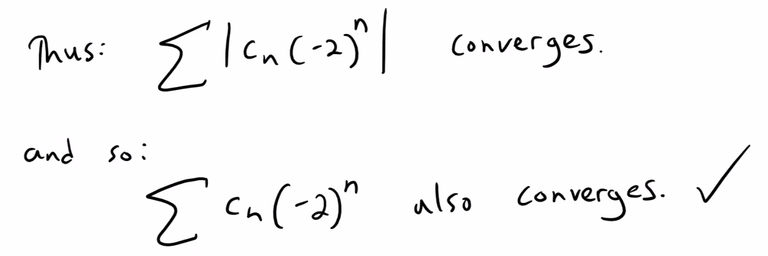
Since it converges absolutely, it therefore converges as per the earlier theorem from Question 6.
Question 5
If ∑ cn6n is convergent, then ∑ cn(-6)n is convergent.
Solution: False
Note that the radius of convergence theorem doesn't help us:
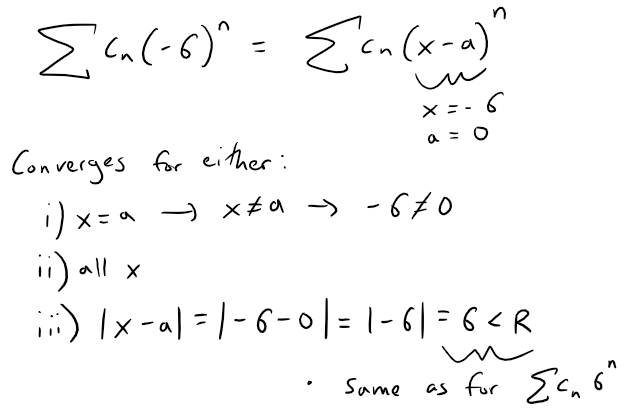
This doesn't help us because if R = 6, then the series could converge at x = 6 but not at x = -6.
In other words, the radius of convergence doesn't help us at the endpoints.
Instead, we can modify both series as follows:
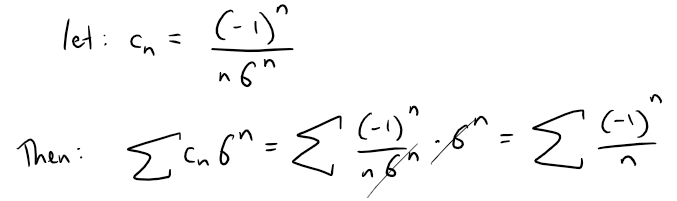
We can apply the Alternating Series Test:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-alternating-tests

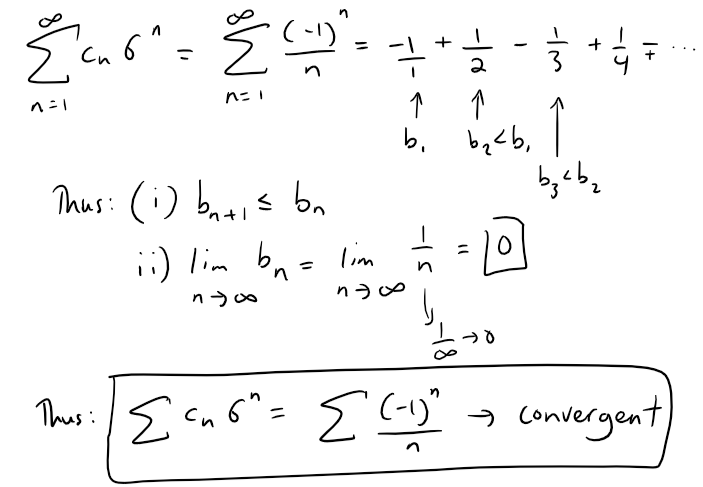
If we do the same for the other series we have:
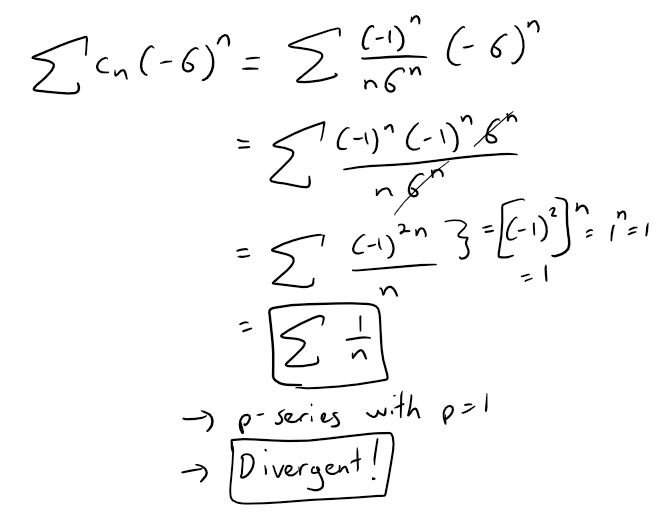
Question 6
If ∑ cnxn diverges when x = 6, then it diverges when x = 10.
Solution: True
As per the radius of convergence theorem, the series diverges as per case (iii):
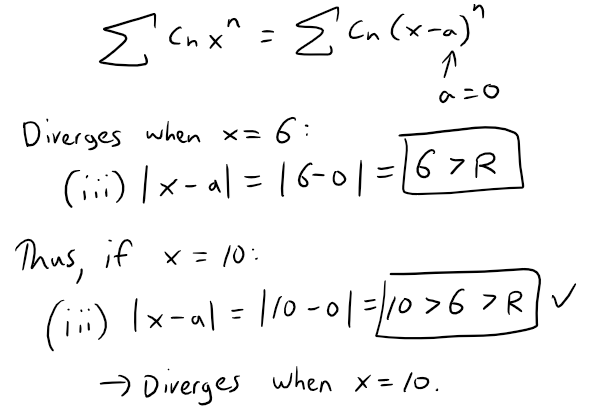
Question 7
The Ratio Test can be used to determine whether ∑ 1/n3 converges.
Solution: False
Recall the Ratio Test from my earlier video:

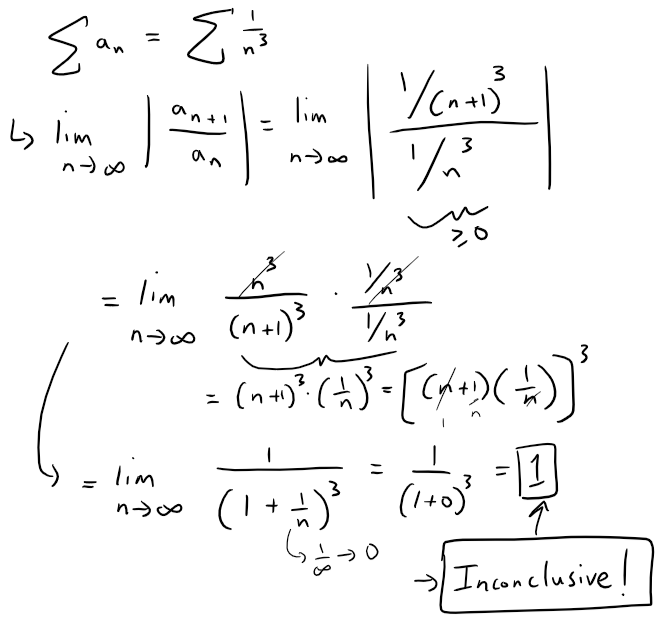
Question 8
The Ratio Test can be used to determine whether ∑ 1/n! converges.
Solution: True
Let's see what the Ratio Test gives us:
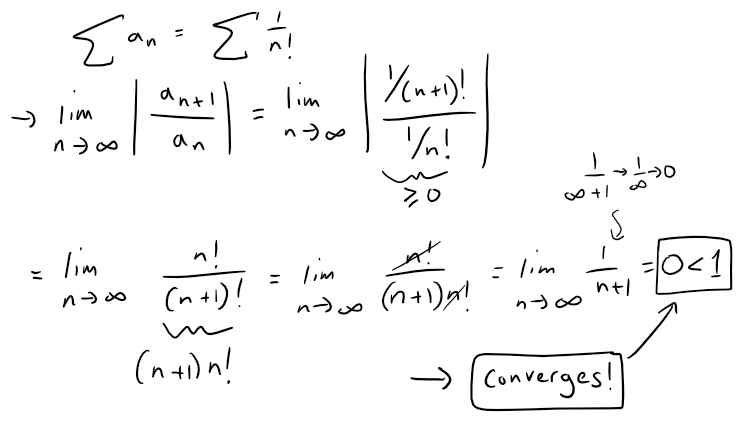
Question 9
If 0 ≤ an ≤ bn and ∑ bn diverges, then ∑ an diverges.
Solution: False
The terms of the series being tested, for the Comparison Test, must be larger than those of a divergent series (or smaller than those of a convergent series). Otherwise, no useful information is obtained.
Question 10
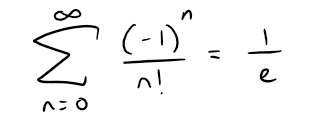
Solution: True
Recall from the earlier table above:
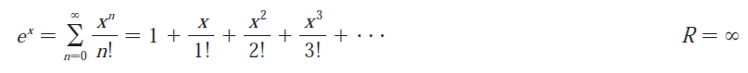
Thus:

Question 11
If -1 < α < 1, then limn→∞ αn = 0.
Solution: True
Recall from my earlier video:
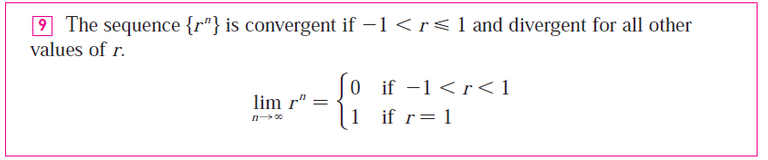
The sequence an = rn can be seen visually for different values of r.
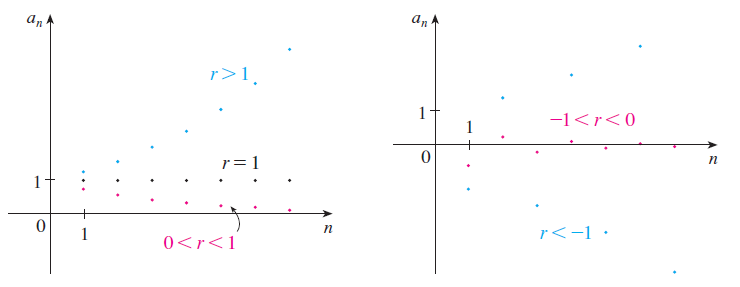
Question 12
If ∑ an is divergent, then ∑ |an| is divergent.
Solution: True
This is true because if it wasn't then, ∑ |an| would be (absolutely) convergent, hence ∑ an also converges; hence we have a contradiction.

But we are given that ∑ an is divergent thus ∑ |an| has to be divergent too.
Question 13
If the series:
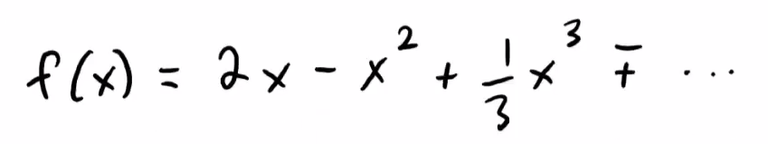
converges for all x, then f'''(0) = 2.
Solution: True
Solution 1: Coefficients of a Power Series
Recall the formula for the coefficients of a power series:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-power-series

Thus, in our case we only need to consider the 3rd (n = 3) coefficient:
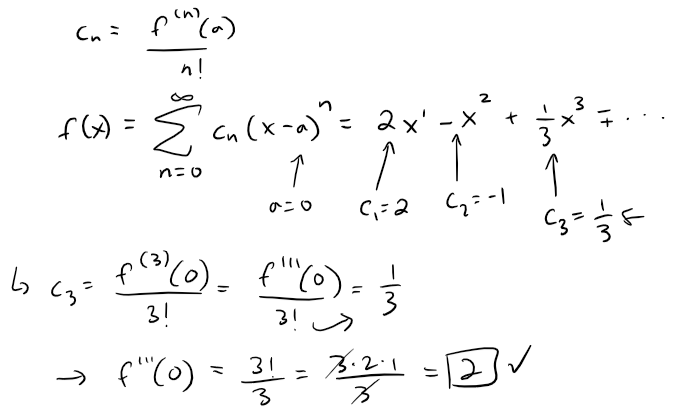
Solution 2: Differentiating f
We can also just take the derivative 3 times and plug in x = 0.
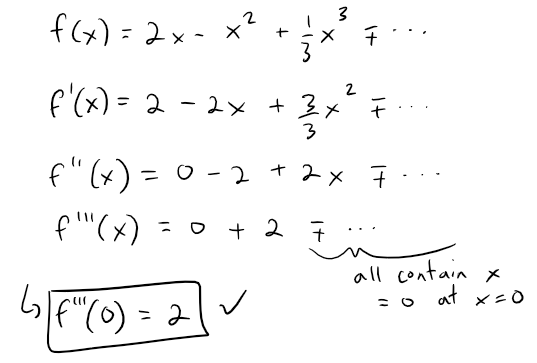
Question 14
If {an} and {bn} are divergent, then {an + bn} is divergent.
Solution: False
We can consider a simple case where 2 divergent sequences cancel each other out, thus giving a convergent sequence.
Let an = n and bn = -n.
{an} and {bn} are divergent.
an + bn = n + (-n) = n - n = 0.
Thus {an + bn} is convergent.
Question 15
If {an} and {bn} are divergent, then {anbn} is divergent.
Solution: False
We can consider another simple case:
Let an = bn = (-1)n
{an} and {bn} are divergent.
anbn = (-1)n (-1)n = (-1)n+n = (-1)2n = [(-1)2]n = 1n = 1
Thus {anbn} is convergent.
Question 16
If {an} is decreasing and an > 0 for all n, then {an} is convergent.
Solution: True
Since {an} is decreasing, it is monotonic, and bounded between 0 < an ≤ a1, then it is convergent as per the Monotonic Sequence Theorem.

Question 17
If an > 0 and ∑ an converges, then ∑ (-1)n an converges.
Solution: True
Note that ∑ (-1)n an is absolutely convergent, hence convergent.
∑ | (-1)n an | = ∑ |(-1)n| an = ∑ an which converges.
Question 18
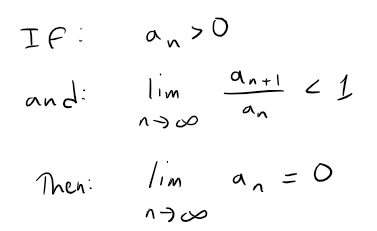
Solution: True
Since an > 0, we can apply the ratio test and find that ∑ an converges.

Thus limn→∞ an = 0 as per the earlier theorem.

Question 19
0.99999... = 1
Solution: True
We can write this as a geometric series:

We can sum this up using the formula for the sum of a geometric series:
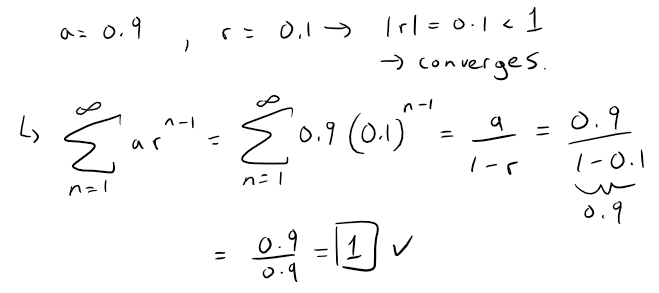
Question 20
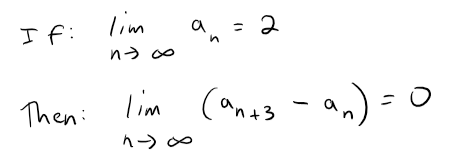
Solution: True
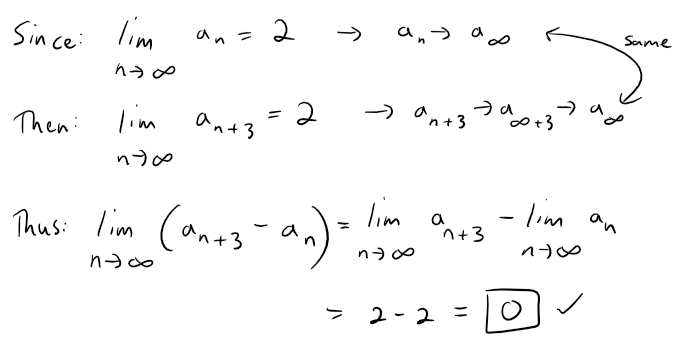
Question 21
If a finite number of terms are added to a convergent series, then the new series is still convergent.
Solution: True
A finite number of terms doesn't affect convergence or divergence of a series.
Question 22
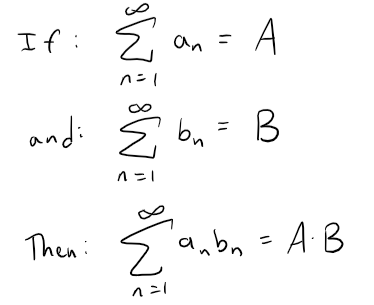
Solution: False
Let's use some basic geometric series to test this out.