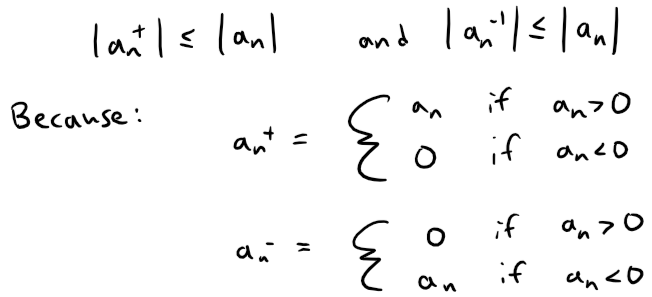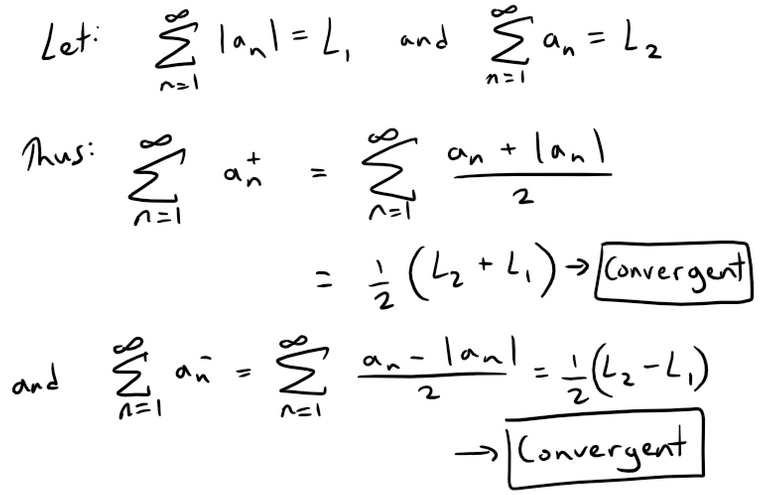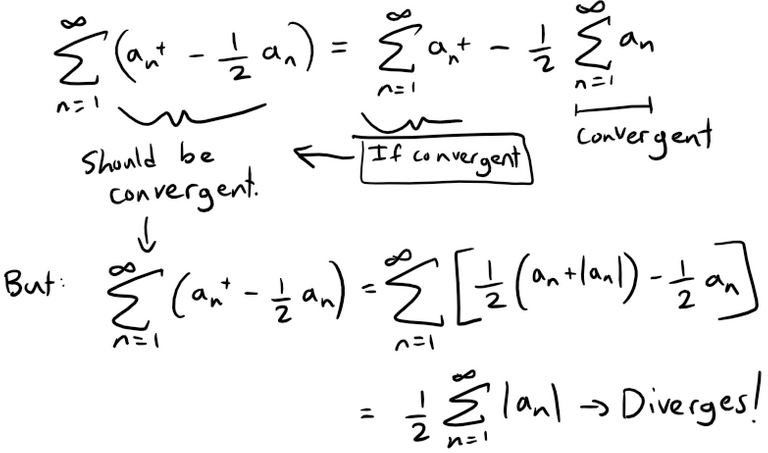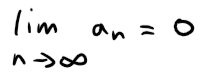Infinite Sequences and Series: Absolute Convergence and the Ratio/Root Tests
In this video I explore further into Infinite Sequences and Series and this time consider series that have involve the absolute values of a sequence. This involves the concept of “absolute convergence” which I show that it implies convergence in general; although the reverse is not always the case. In this case, the very interesting concept of “conditional convergence” arises which allows for the convergence of a series simply by re-arranging the terms such that the positive and negative terms cancel out; which is only possible if a series is not absolutely convergent. I also go over two specific tests to determine absolute convergence and they are the ratio and root test which are as their names describe. Half of this video is spent on 4 exercises at the end of the video and are a great way to reinforce the concepts introduced in this video.
The topics and their timestamps in the video are listed below:
- @ 1:59 - Absolute Convergence
- @ 2:43 - Definition 1
- @ 3:46 - Example 1
- @ 5:53 - Example 2
- Conditional Convergence
- @ 9:22 - Definition 2
- @ 9:54 - Theorem 1
- @ 14:34 - Example 3
- @ 20:46 - The Ratio Test
- @ 44:48 - Example 4
- @ 50:37 - Note on Estimating Sums
- @ 51:21 - Example 5
- @ 58:51 - Note on the Ratio Test
- @ 1:01:25 - The Root Test
- @ 1:05:15 - Example 6
- @ 1:08:46 - Rearrangements
- Exercises
- @ 1:24:52 - Exercise 1
- @ 1:47:01 - Exercise 2: Proof of the Root Test
- @ 2:12:30 - Exercise 3
- @ 2:28:40 - Exercise 4
Please note the following list of corrections which I realized during the making of the video:
- @ 21:50 – Forgot to include the other condition of part (ii) of the Root Test: limn→∞ |an+1/an| = ∞. Note that in the video I corrected this @ 36:02 during the proof of part (ii).
- @ 2:42:42 - Should’ve written |s9 – r| = |1 – 5| = 4 < |a9| and also should've shown that we can ensure this to be the case regardless of the value of a9.
Watch Video On:
- 3Speak: https://3speak.tv/watch?v=mes/koaskori
- Odysee: https://odysee.com/@mes:8/sequences-and-series-Absolute-Convergence-ratio-root-tests:8
- BitChute: https://www.bitchute.com/video/LR66CS0EMIOg/
- Rumble: https://rumble.com/v1ybd1c-infinite-sequences-and-series-absolute-convergence-and-the-ratioroot-tests.html
- DTube: https://d.tube/#!/v/mes/QmVrfvYJoKrTdhkWwKERdYQyZKMkk2FpxkkcufeyBdvSPH
- YouTube: https://youtu.be/3V7yXjayNB8
Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIh_NXBMhbCTS1dvztYg?e=EZPQ9u
View Video Notes Below!
Download These Notes: Link is in Video Description.
View These Notes as an Article: https://peakd.com/@mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of My Videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight Back Against Censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord Chat Room: https://mes.fm/chatroom
Check out my Reddit and Voat Math Forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
Watch my #AntiGravity Video Series: https://peakd.com/antigravity/@mes/series
- See Part 6 for my Self Appointed PhD and #MESDuality Breakthrough Concept!
Follow My #MESExperiments Video Series: https://peakd.com/mesexperiments/@mes/list
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (If Available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ Speed by Browser Extensions or Modifying Source Code.
-- Browser Extension Recommendation: https://mes.fm/videospeed-extension
-- See my tutorial to learn more: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and Read Notes.
- Read notes on Steemit #GetOnSteem
- Watch the video in parts.
NOTE #2: If video volume is too low at any part of the video:
- Download this Browser Extension Recommendation: https://mes.fm/volume-extension
Infinite Sequences and Series: Absolute Convergence and the Ratio and Root Tests

Calculus Book Reference
Note that I mainly follow along the following calculus book:
- Calculus: Early Transcendentals Sixth Edition by James Stewart
Topics to Cover
- Absolute Convergence
- Definition 1
- Example 1
- Example 2
- Conditional Convergence
- Definition 2
- Theorem 1
- Example 3
- The Ratio Test
- Example 4
- Note on Estimating Sums
- Example 5
- Note on the Ratio Test
- The Root Test
- Example 6
- Rearrangements
- Exercises
- Exercise 1
- Exercise 2: Proof of the Root Test
- Exercise 3
- Exercise 4
Absolute Convergence
Given any series ∑ an, we can consider the corresponding series:
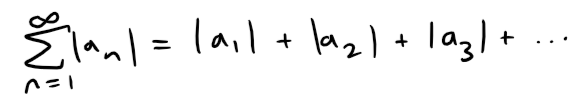
whose terms are the absolute values of the terms of the original series.
Definition 1
A series ∑ an is called absolutely convergent if the series of absolute values ∑ |an| is convergent.
Notice that if ∑ an is a series with positive terms, then |an| = an and so absolute convergence is the same as convergence in this case.
Also note that in my earlier videos I went over convergence tests for series with positive terms and for alternating series.
But what if the signs of the terms switch back and forth irregularly?
We will see in Example 3 later in this video that the idea of absolute convergence sometimes helps in such cases.
Example 1
The series:
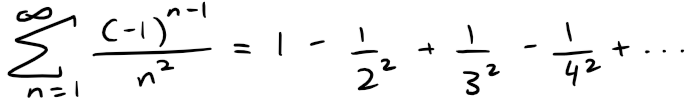
is absolutely convergent because:

is a convergent p-series (p = 2).
Recall the p-series from my earlier video.
Retrieved: 26 August 2019
Archive: http://archive.fo/vapHa
Example 2
We know, from my earlier video, that the alternating harmonic series:
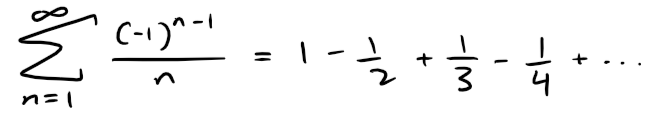
is convergent.
Recall from my earlier video on alternating series.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-alternating-tests
Retrieved: 26 August 2019
Archive: http://archive.fo/9neM8


Although the alternating harmonic series is convergent, it not absolutely convergent because the corresponding series of absolute values is:
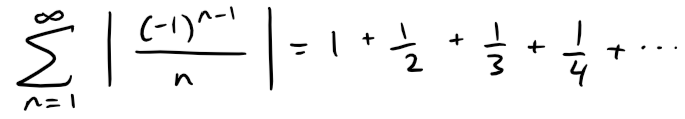
which is the harmonic series (p-series with p = 1) and is therefore divergent.
Conditional Convergence
Definition 2
A series ∑ an is called conditionally convergent if it is convergent but not absolutely convergent.
Example 2 shows that the alternating harmonic series is conditionally convergent.
Thus it is possible for a series to be convergent but not absolutely convergent.
However, the next theorem shows that absolute convergence implies convergence.
Theorem 1
If a series ∑ an is absolutely convergent, then it is convergent.
Proof:
Observe that the inequality:

is true because |an| is either an or -an.
If ∑ an is absolutely convergent then ∑ |an| is convergent, so ∑ 2|an| is convergent.
Therefore, by the Comparison Test, ∑ (an + |an|) is convergent.
Recall the Comparison Test from my earlier video.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-comparison-tests
Retrieved: 26 August 2019
Archive: http://archive.fo/f0SM5
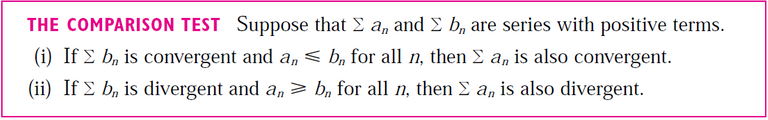
Then:

is the difference of two convergent series and is therefore convergent.
Example 3
Determine whether the series:
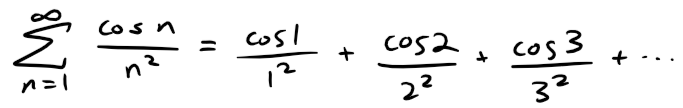
is convergent or divergent.
Solution:
This series has both positive and negative terms, but it is not alternating.
The first term is positive, the next three are negative, and the following three are positive: The signs change irregularly.
Calculation Check:
- Note that my Calculus Book used Radians and my OneNote uses Degrees so I need to convert degrees to radians: half a circle is 180 degrees = π radians)
- cos(1*180/pi)/1^2 = 0.54030230586814
- cos(2*180/pi)/2^2 = -0.104036709136786
- cos(3*180/pi)/3^2 = -0.109999166288938
- cos(4*180/pi)/4^2 = -0.0408527263039757
- cos(5*180/pi)/5^2) = 0.011346487418529
- cos(6*180/pi) = 0.960170286650366
- cos(7*180/pi) = 0.753902254343305
- cos(8*180/pi) = -0.145500033808614
We can apply the Comparison Test to the series of absolute values:
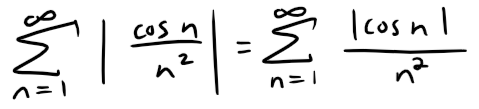
Since |cos n| ≤ 1 for all n, we have:
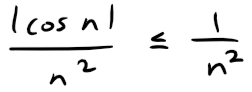
We know that ∑ 1/n2 is convergent (p-series with p = 2) and therefore ∑ |cos n|/n2 is convergent by the Comparison Test.
Thus the given series ∑ (cos n)/n2 is absolutely convergent and therefore convergent by Theorem 1.
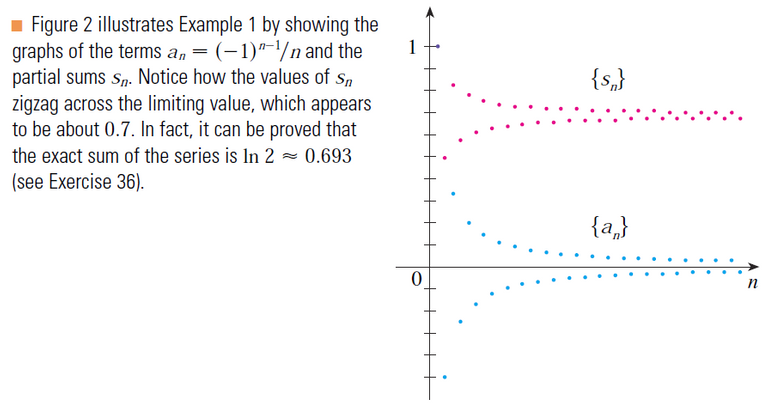
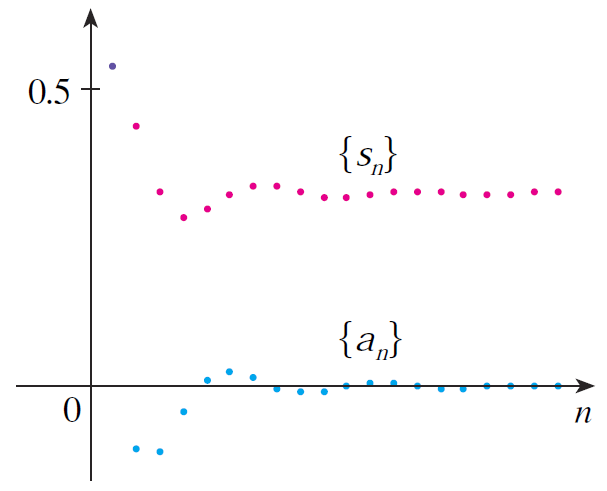
The figure below shows the graphs of the terms an and partial sums sn of the series in Example 3.
Notice that the series is not alternating but has positive and negative terms.
The following test is very useful in determining whether a given series is absolutely convergent.
The Ratio Test
(i) If:
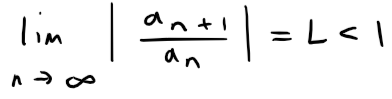
then the series ∑∞n=1 an is absolutely convergent (and therefore convergent).
(ii) If:
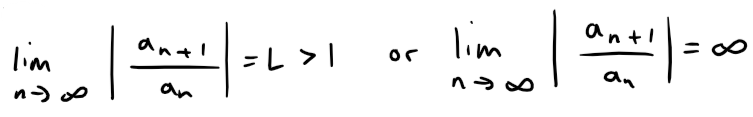
then the series ∑∞n=1 an is divergent.
(iii) If:
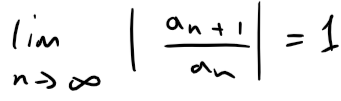
then the Ratio Test is inconclusive; that is no conclusion can be drawn about the convergence or divergence of ∑ an.
Proof:
(i) The idea is to compare the given series with a convergent geometric series.
Recall the geometric series from my earlier video on Infinite Series.
Retrieved: 27 July 2019
Archive: http://archive.fo/FGAyJ
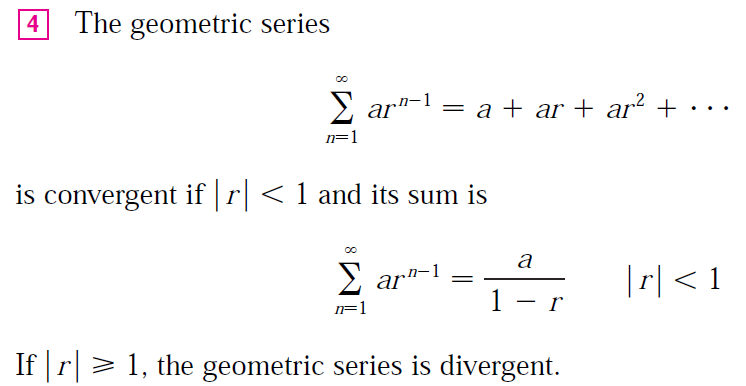
Since L < 1, we can choose a number r such that L < r < 1.
Since:
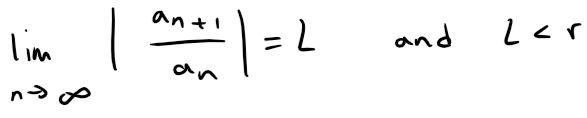
the ratio |an+1/ an| will eventually be less than r; that is, there exists an integer N such that:

Or, equivalently,
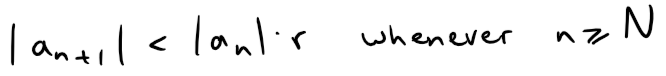
Putting n successively equal to N, N + 1, N + 2, … in the above inequality, we obtain:
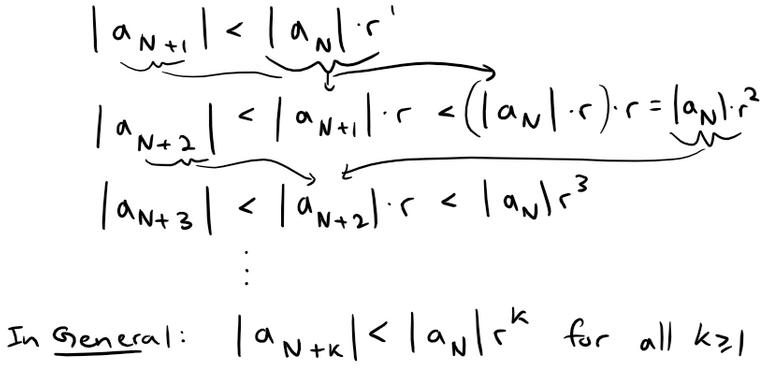
Now the series:
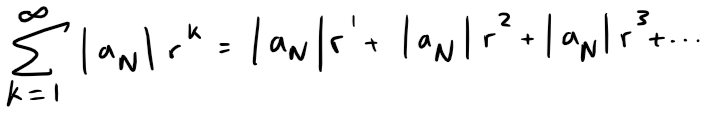
is convergent because it is a geometric series with 0 < r < 1.
So the general inequality above, together with the Comparison Test, shows that the series:

is also convergent.
It follows that the series ∑∞n=1 |an| is convergent.
Recall that a finite number of terms doesn't affect convergence.
Therefore ∑ an is absolutely convergent (and therefore convergent).
(ii) If:
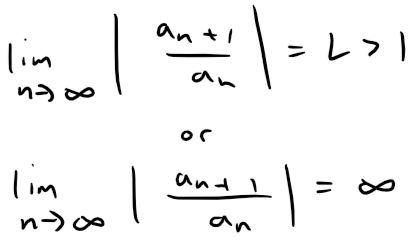
then the ratio |an+1/ an| will eventually be greater than 1; that is, there exists an integer N such that:

This means that:
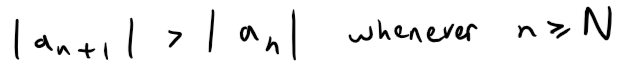
and so:

Therefore ∑ an diverges by the Test for Divergence.
Recall the Test for Divergence also from my earlier video on Infinite Series.
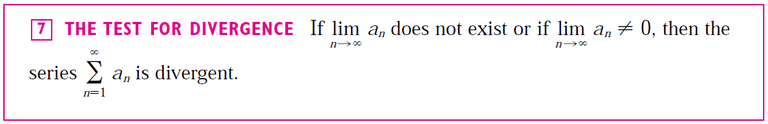
Note: Part (iii) of the Ratio Test says that if:
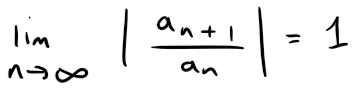
then the test gives no information.
For instance, for the convergent series ∑ 1/n2 we have:
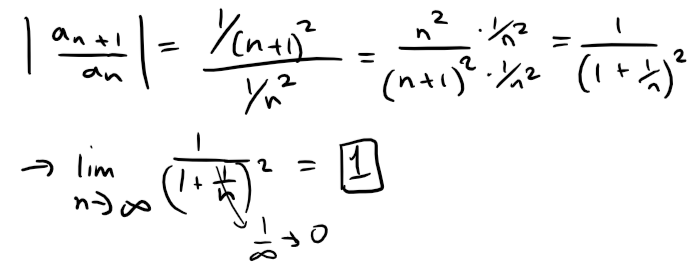
whereas for the divergent series ∑ 1/n we have:

Therefore, if limn→∞ |an+1/ an| = 1 the series ∑ an might converge or it might diverge.
In this case the Ratio Test fails and we must use some other test.
Example 4
Test the following series for absolute convergence:
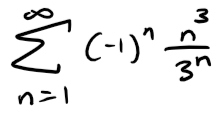
Solution:
We use the Ratio Test with:

Thus, by the Ratio Test, the given series is absolutely convergent and therefore convergent.
Note on Estimating Sums
In my earlier videos we used various methods for estimating the sum of a series - the method depended on which test was used to prove convergence.
What about series for which the Ratio Test works?
There are two possibilities:
If the series happens to be an alternating series, as in Example 4, then it is best to use the methods of my earlier video on alternating series.
If the terms are all positive, then we can use the special methods explained in Exercise 1 later in this video.
Example 5
Test the convergence of the series:
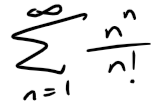
Solution:
Since the terms an = nn / n! are positive, we don't need the absolute value signs.
Recall from my earlier video that this is in fact the number e written as a limit. Retrieved: 26 August 2019 The Theorem 2.5.8 mentioned in the above proof is shown in my other earlier video. #EarlierVideos Retrieved: 26 August 2019 Since e > 1, the given series is divergent by the Ratio Test. Although the Ratio Test works in Example 5, an easier method is to use the Test for Divergence. Since: It follows that an does not approach 0 as n → ∞. Therefore the given series is divergent by the Test for Divergence. The following test is convenient to apply when n-th powers occur. Its proof is similar to the proof of the Ratio Test and shown in Exercise 2 later in this video. (i) If: then the series ∑∞n=1 an is absolutely convergent (and therefore convergent). (ii) If: then the series ∑∞n=1 an is divergent. (iii) If: then the Root Test is inconclusive. If limn→∞ |an|1/n then part (iii) of the Root Test says that the test gives no information. The series ∑ an could converge or diverge. If L = 1 in the Ratio Test, don't try the Root Test because L will again be 1. And if L = 1 in the Root Test, don't try the Ratio Test because it will fail too. Test the convergence of the series: Solution: Thus the given series converges by the Root Test. The question of whether a given convergent series is absolutely convergent or conditionally convergent has a bearing on the question of whether infinite sums behave like finite sums. If we rearrange the order of the terms in a finite sum, then of course the value remains unchanged. But this is not always the case for an infinite series. By a rearrangement of an infinite series ∑ an we mean a series obtained by simply changing the order of the terms. For instance, rearrangement of ∑ an could start as follows: It turns out that: If ∑ an is an absolutely convergent series with sum s, then any rearrangement of ∑ an has the same sum s. However, any conditionally convergent series can be rearranged to give a different sum. To illustrate this fact let's consider the alternating harmonic series: Recall that this summation is proved in my earlier video on alternating tests. https://peakd.com/mathematics/@mes/infinite-sequences-and-series-alternating-tests If we multiply this series by 1/2, we get: Inserting zeros between the terms of the series, we have: Note that adding these zeroes does not affect the sum of the series; each term in the sequence of partial sums is repeated, but the limit is the same. Now we add the series 1 and 2 using the theorem also from my earlier video on infinite series. Thus we have: Notice that the above series contains the terms as in series 1, but rearranged so that one negative term occurs after each pair of positive terms. The sums of these series, however, are different. In fact, Riemann proved that: If ∑ an is a conditionally convergent series and r is any real number whatsoever, then there is a rearrangement of ∑ an that has a sum equal to r. A proof of this fact is outline in Exercise 4. Let ∑ an be a series with positive terms and let rn = an+1/ an.
Suppose that limn→∞ rn = L < 1, so ∑ an converges by the Ratio Test.
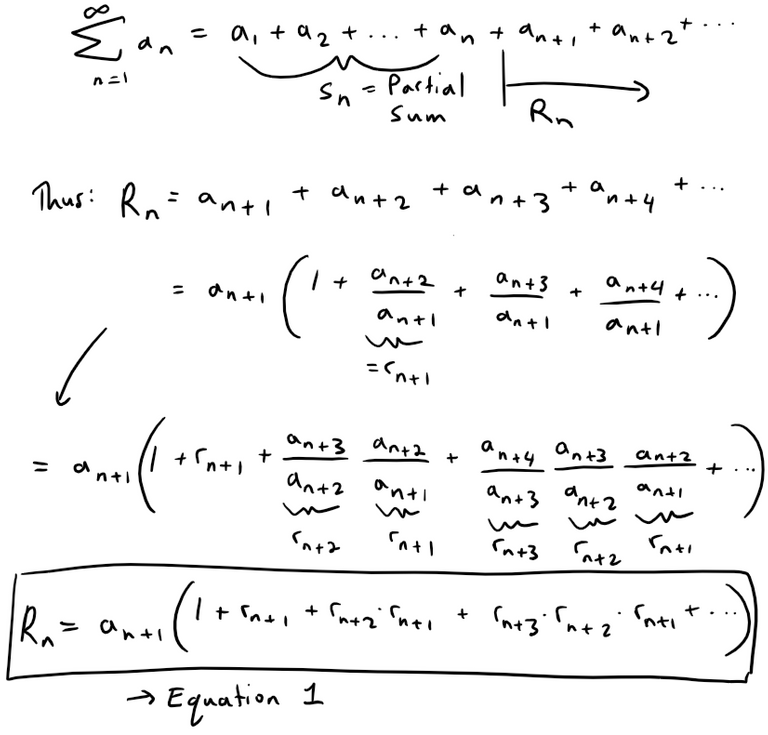
As usual, we let Rn be the remainder after n terms, that is: (a) If {rn} is a decreasing sequence and rn+1 < 1, show, by summing a geometric series, that:
(b) If {rn} is an increasing sequence, show that:
Solution: (a) The remainder is: Since {rn} is decreasing we have:
Since rn+1 < 1 thus we have that Rn is less than a convergent Geometric Series:
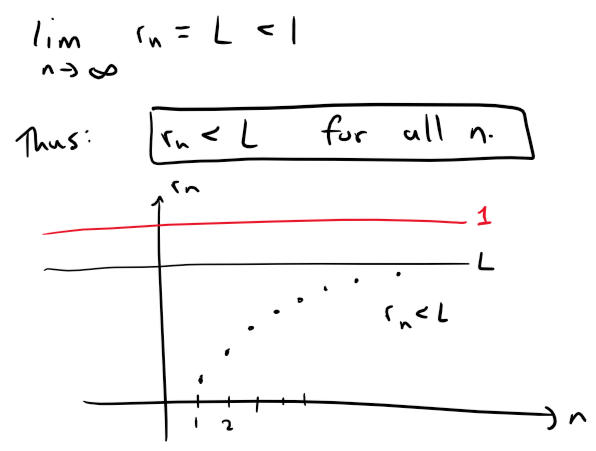
(b) Note that since {rn} is increasing and given that:
So, starting with Equation 1 from (a), we have: And since L < 1 we have that the Remainder again is less than a Geometric Series: Prove the Root Test. Hint for part (i): Take any number r such that L < r < 1 and use the fact that there is an integer N such that: Solution: Recall the Root Test from earlier in this video: (i) Following the hint, we get that: Since 0 ≤ L < 1 and L < r < 1, we have 0 < r < 1 and thus the following geometric series converges: Since |an| < rn for n ≥ N, by the Comparison Test:
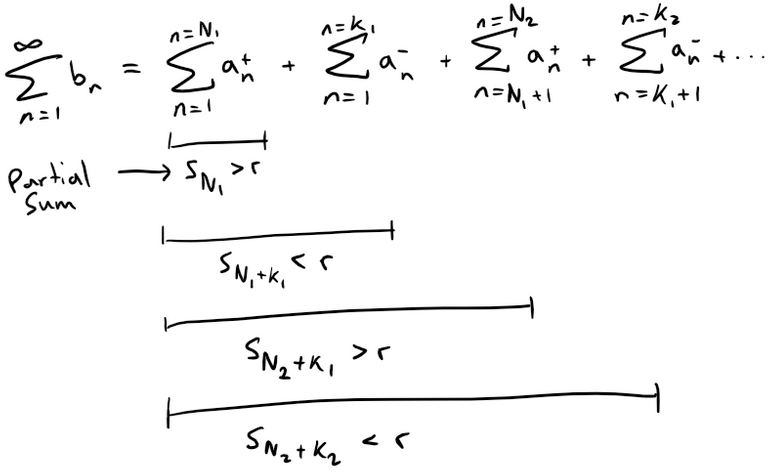
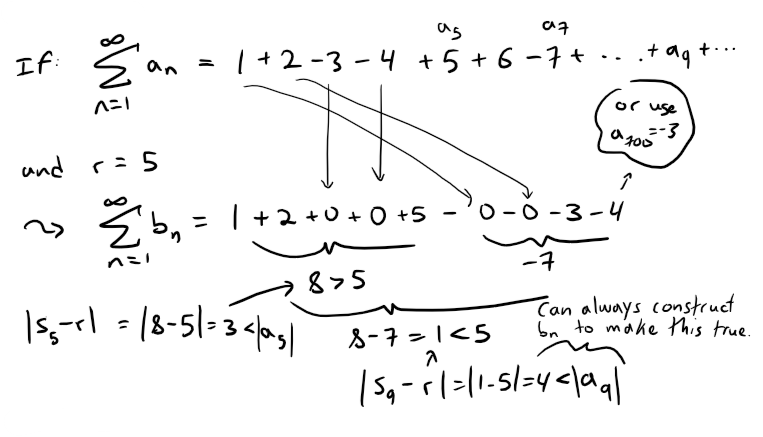
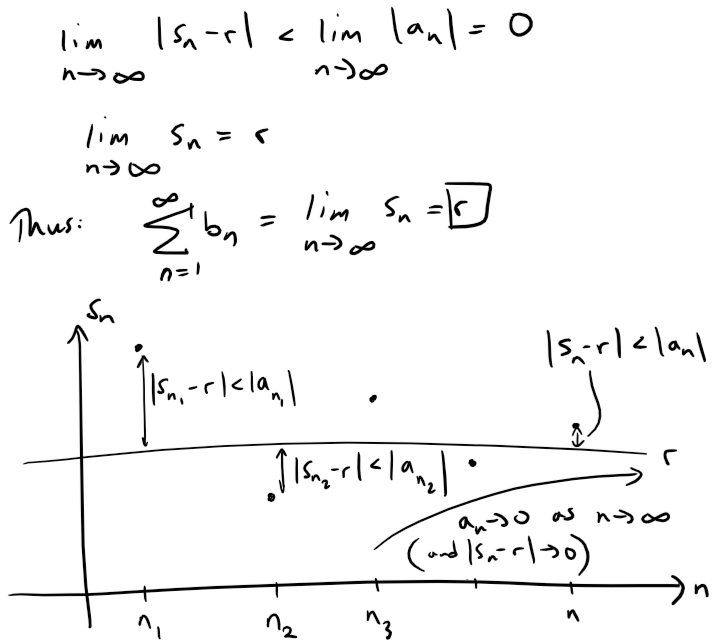
And since convergence does not depend on a finite number of terms, we have: And thus: (ii) Since: then there is an integer N such that: Thus we have: (iii) Consider the following two series: Divergent harmonic p-series (p = 1): If this limit exists then we have: Similarly for the convergent p-series (p = 2): For each, sum: so the Root Test is inconclusive. Given any series ∑ an, we define a series ∑ a+n whose terms are all the positive terms of ∑ an and a series ∑ a-n whose terms are all the negative terms of ∑ an. To be specific, we let: Notice that if an > 0, then a+n = an and a-n = 0, whereas if an < 0, then a-n = an and a+n = 0. (Pretty ingenious when you think about it.) (a) If ∑ an is absolutely convergent, show that both of the series ∑ a+n and ∑ a-n are convergent. (b) If ∑ an is conditionally convergent, show that both of the series ∑ a+n and ∑ a-n are divergent. Solution: (a) Since ∑ an is absolutely convergent, and since: we thus conclude by the Comparison Test that both ∑ a+n and ∑ a-n must be absolutely convergent. Note: We can also solve Part (a) as follows: (b) We will show by contradiction that both ∑ a+n and ∑ a-n must diverge. For suppose that ∑ a+n converged. Then so would the following series converge: Note that ∑ |an| diverges because ∑ an is only conditionally convergent. Hence, ∑ a+n can't converge. Similarly, neither can ∑ a-n. Exercise 4 Prove that if ∑ an is a conditionally convergent series and r is any real number, then there is a rearrangement of ∑ an whose sum is r. Hints: (1) Use the notation of Exercise 3. (2) Take just enough positive terms a+n so that their sum is greater than r. (3) Then add just enough negative terms a-n so that the cumulative sum is less than r. (4) Continue in this manner and use the following theorem also from my earlier video: Solution: Let ∑ bn be the rearranged series constructed in the hint. Note that this series can be constructed this way by virtue of the result from Exercise 3b which states that if ∑ an is conditionally convergent than both ∑ a+n and ∑ a-n are divergent; hence we can keep adding their terms to obtain as large of a number we want since there is no limit. This series ∑ bn will have partial sums sn that oscillate in value back and forth across r. Since ∑ an is convergent, we can apply the given theorem from my earlier video: We can ensure that our construction of ∑ bn has oscillations |sn - r| that are always less than |an|, for example: Thus we have that:
Archive: http://archive.fo/sJyuL
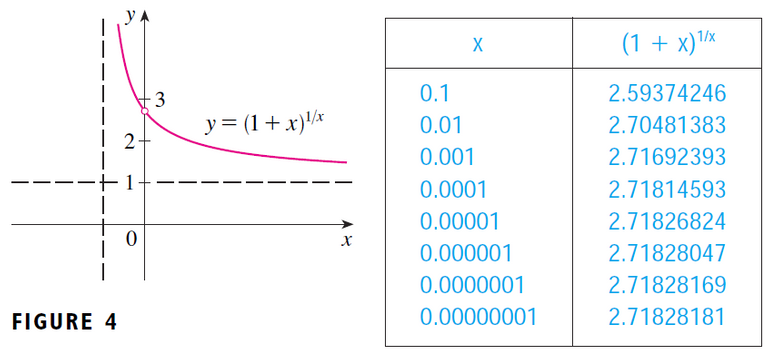
Archive: http://archive.fo/035sm
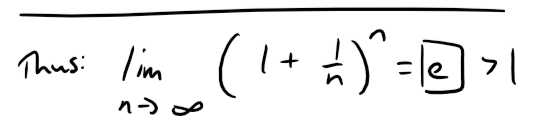
Note on the Ratio Test
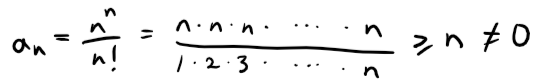
The Root Test
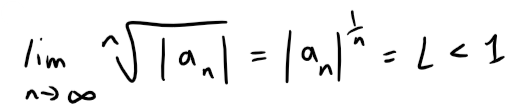


Example 6

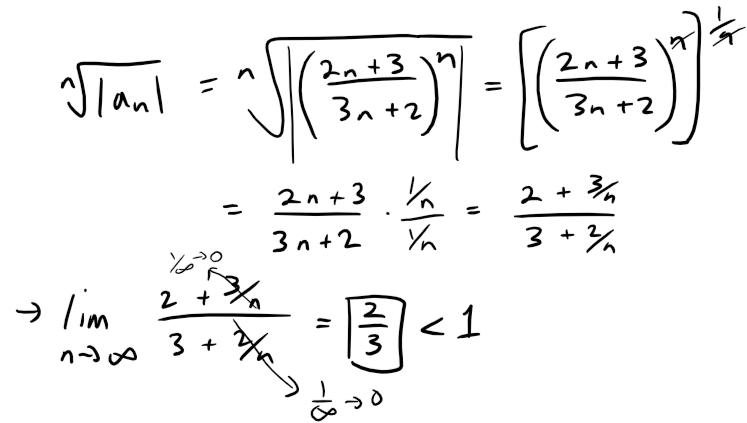
Rearrangements
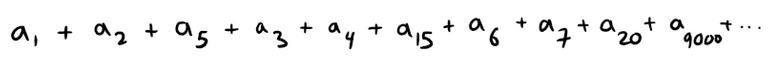
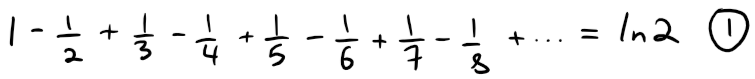
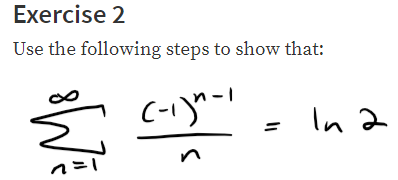

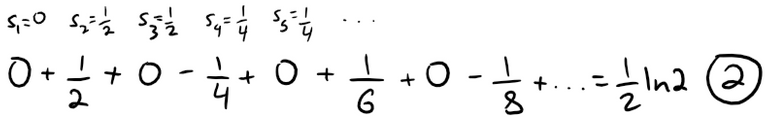
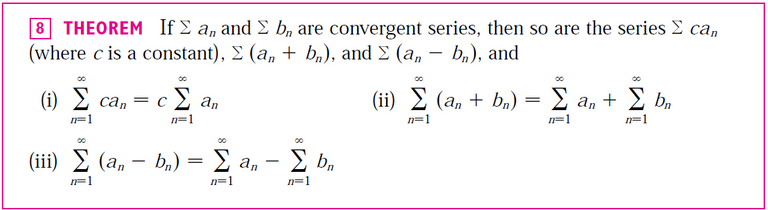

Exercises
Exercise 1
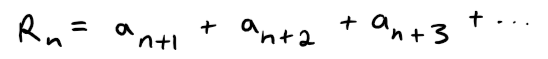
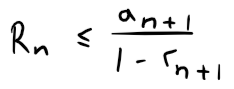



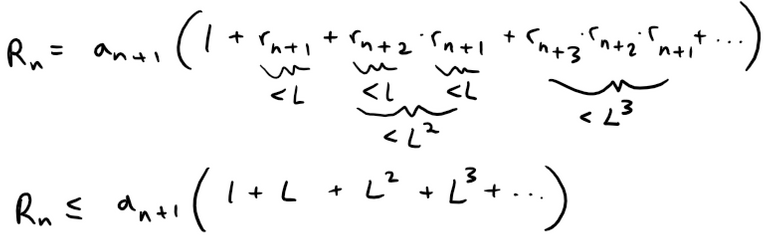
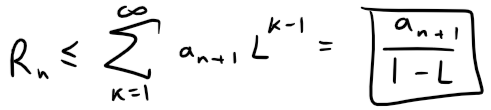
Exercise 2: Proof of the Root Test




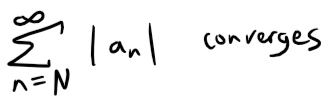


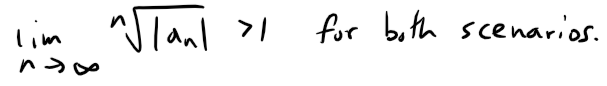
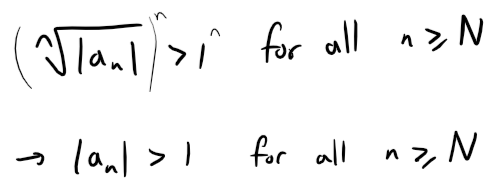

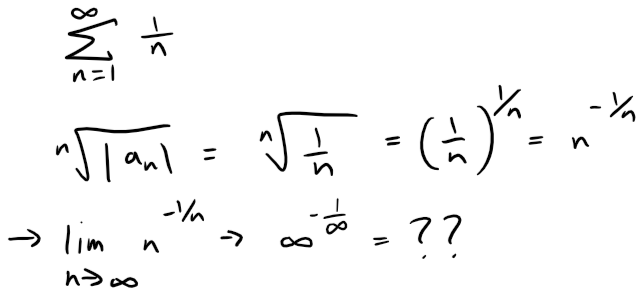



Exercise 3