Physics - Classical Mechanics - Simple Harmonic Motion Exercises

avatar
(Edited)

[Image1]

Introduction

Hey it's a me again @drifter1!

Today we continue with Physics, and more specifically the branch of "Classical Mechanics" in order to get into Simple Harmonic Motion Exercises.

This is also my last post for the year! So, I'm wishing you all happiness and most importantly good health in 2022!

So, without further ado, let's get straight into it!

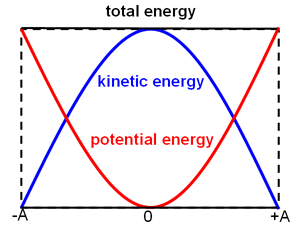
Example 1: Horizontal Oscillator

Let's consider the horizontal mass-spring system shown in the figure below, where the mass is m = 6 Kg and the spring constant is k = 150 N / m.

Calculate the:

  • amplitude (A)
  • phase angle (φ)
  • total energy (E)
  • displacement as a function of time ( x(t) )

for the cases below:

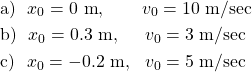
Angular Frequency (ω)

The amplitude (which is needed for most of the variables) can be calculated from the initial velocity v0 and displacement x0, as well as the angular frequency ω, which for now is unknown. So, let's first calculate the angular frequency, as it's the same for all the cases!

In this horizontal spring-mass oscillator the period is :

And thus the angular frequency is given by:

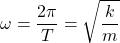
Substituting the known variables gives us:

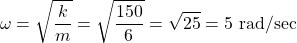
which is a valid value for all the individual cases!

a) x0 = 0 m, v0 = 10 m/sec

As we covered in a previous part, amplitude can be calculated from the following equation:

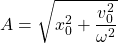
Substituting the known values gives us:

From the Reference Circle, because the initial displacement is 0, the phase angle φ will have to be either π / 2 or 3π / 2. But, the initial velocity is positive, and thus we know that the second is true, meaning:

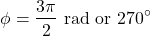
Which is a phase close to the start of the next period. We could also say something like φ = -π / 2 to make it more clear.

Because the initial velocity is also the maximum velocity, the total (or maximum) energy is equal to the kinetic energy at t = 0, which is:

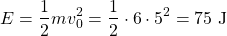
Of course, the same result can also be calculated from potential energy with x = A, which will be the quicker way in the remaining two cases!

Now that everything is known, we can also write the displacement as a function of time:

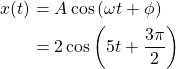
b) x0 = 0.3 m, v0 = 3 m/sec

Using the same equation as previously, we can calculate the amplitude for the second case now:

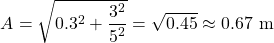
The maximum energy can now be calculated from potential energy:

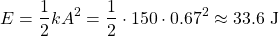
The phase angle is still unknown though, so let's try to calculate it from the displacement equation, which is:

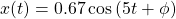
"Plugging in" the known initial value for t = 0, will now give us the phase angle:

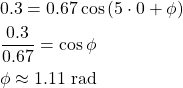
Thus, the displacement equation is:

c) x0 = -0.2 m, v0 = 5 m/sec

Now for the last case...

First of all, the amplitude is equal to:

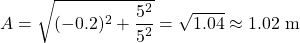
The corresponding total energy is now:

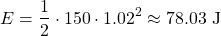
Using the same strategy as in the previous case, the phase angle is:

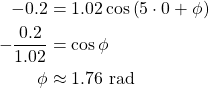
And so the displacement as a function if time can be written as:

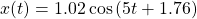
Example 2: Vertical Oscillator

Let's next consider the vertical mass-spring system shown in the figure below, where the mass is m = 5 Kg and the spring constant is k = 405 N / m. The gravitational acceleration is g = 9.8 m / sec 2.

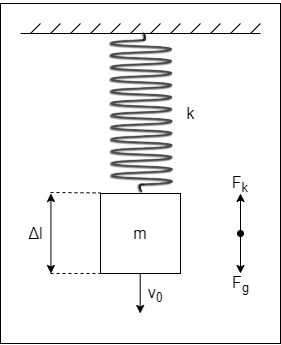
Let's calculate:

  • the stretching of the spring (Δl) when the system is at rest
  • the period (T) if the system is put into oscillation
  • the displacement as a function of time ( y(t) )

For the last one consider only the case:

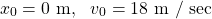
Spring Stretching at Rest (Δl)

The first problem is a quite simple Equilibrium case. Only two forces act upon the object, which are the gravity and the spring's return force. The system is at rest when those two forces are equal. Thus, we have:

Substituting the known values, gives us the spring's stretching:

Oscillation Period (T)

The period is given by the same equation, independent of the spring's orientation! Basically, the spring's return force is larger when the object moves up, and smaller when the object moves down.

Anyway, the period is:

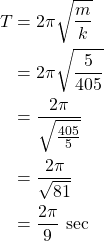
Displacement as a Function of Time ( y(t) )

In order to calculate the displacement we first need to know the amplitude. The amplitude equation requires the angular frequency, so let's first calculate ω:

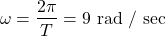
And so, the amplitude is:

From the previous example, we know that the phase angle is φ = 3 π / 2 or -π / 2, when the velocity is maximum positive and the displacment is zero. Let's use the second value this time!

So, at last, the displacement as a function of time is:

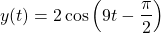
RESOURCES:

Images

  1. https://commons.wikimedia.org/wiki/File:Energy_in_SHM.gif

Mathematical equations used in this article, where made using quicklatex.

Block diagrams and other visualizations were made using draw.io.

Previous articles of the series

Rectlinear motion

Plane motion

Newton's laws and Applications

Work and Energy

Momentum and Impulse

Angular Motion

Equilibrium and Elasticity

Gravity

Periodic Motion

Final words | Next up

And this is actually it for today's post!

Next time we will cover Simple Pendulums...

See ya!

Keep on drifting!

Posted with STEMGeeks

physics science education mechanics simple harmonic motion exercises examples stem
0
0
0.000
0 comments