Sum Of Two Dice Probabilities With R & Python Programming
Hi there. In this post, I cover probabilities for the sum of two dice with the use of R & Python programming. The screenshots in this post are outputs from my Rstudio program and from my Jupyter Notebook.
For the dice they are the standard usual dice with six sides each. They are numbered 1 to 6 each.

R Programming For The Sum Of Two Dice Probabilities
I found that with R, computing the probabilities for the sum of two dice not too bad. There are a few functions in R that are a bit niche or specialized such as expand.grid, and cumsum().
Initialize a six sided die with dice <- seq(1, 6). The combination of two dice can be obtained with the use of expand.grid(). Expand grid is obtaining the Cartesian product for those who know math and basic set theory. I then add the numbers from the combinations to create the Sum column. The table is converted into a data frame.
# Combination of dice
two_dice <- data.frame(expand.grid(dice, dice))
two_dice$Sum <- two_dice$Var1 + two_dice$Var2
# Compute probabilities:
occurrences <- data.frame(table(two_dice$Sum))
# Show occurrences:
occurrences
The column names are then renamed with:
# Change Var1 Column:
colnames(occurrences) <- c('Sum_TwoDice', 'Frequency')
The number of total combinations from rolling two dice is 36. This is from 6 times 6. Probabilities are obtained with the frequency counts divided by 36. I round the probabilities to 3 decimal places with round().
# Create probability column: Frequency / #combinations (36)
occurrences$Probability <- round(occurrences$Frequency / 36, 3)
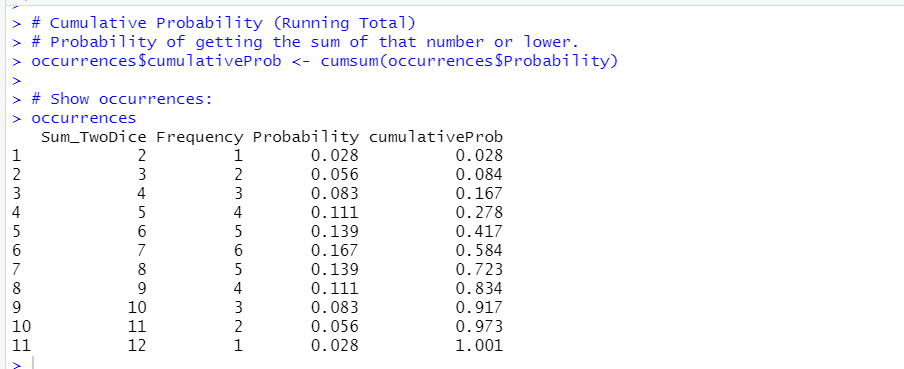
The probabilities column is the probability of getting a particular sum of two dice. I add a cumulative probability column for probabilities of getting a sum of a number or lower. In math notation it would be represented by something like Prob(Sum less than or equal to Value)
# Cumulative Probability (Running Total)
# Probability of getting the sum of that number or lower.
occurrences$cumulativeProb <- cumsum(occurrences$Probability)
# Show occurrences:
occurrences
Python Programming For Sum of Two Dice Probabilities
In Python, I found that it did take longer for me to get the probabilities in a table. I had to do trial and error with some of the pandas function. Start with import pandas as pd and initialize a die with die = range(1, 7).
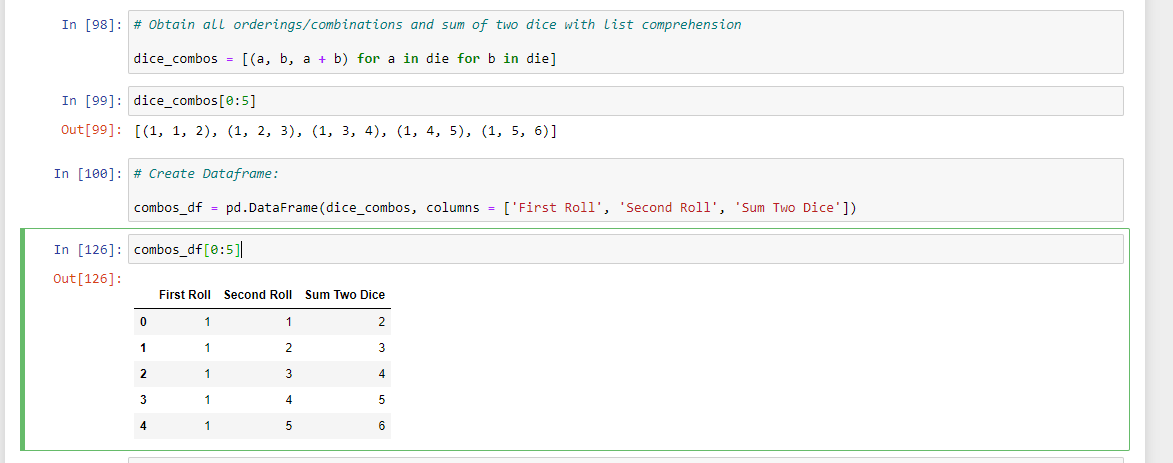
A nice way of obtaining the two dice combinations and sum is with the use of list comprehension. Instead of running two for loops and appending values into a list, it is better to use list comprehension.
die = range(1, 7)
# Obtain all orderings/combinations and sum of two dice with list comprehension
dice_combos = [(a, b, a + b) for a in die for b in die]
dice_combos[0:5]
Dice combinations along with their sums are converted into a pandas dataframe.
# Create Dataframe:
combos_df = pd.DataFrame(dice_combos, columns = ['First Roll', 'Second Roll', 'Sum Two Dice'])
combos_df[0:5]
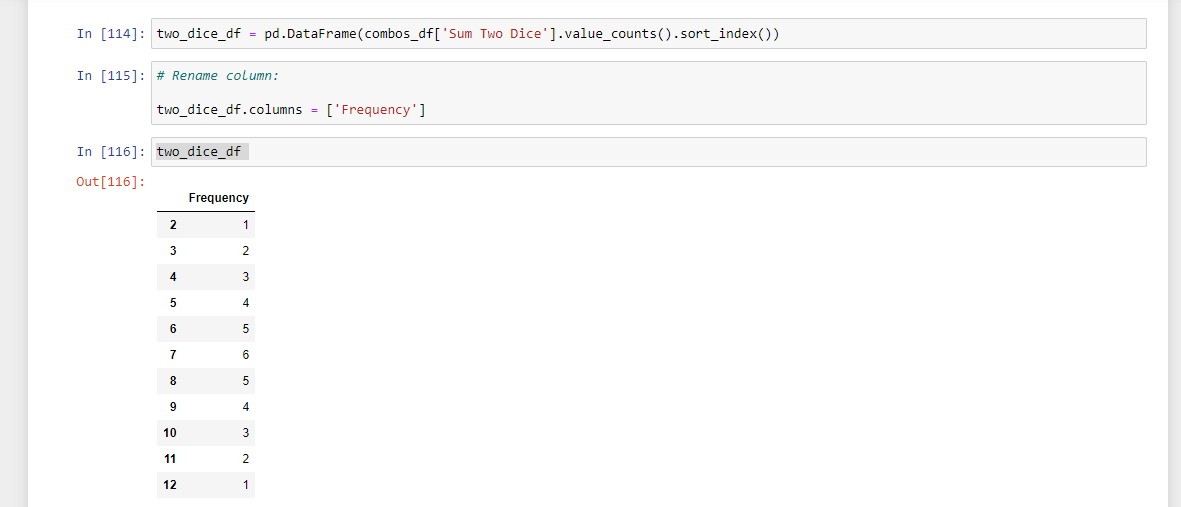
Next, I want to find the frequencies of the sum of two dice in Python & pandas. I use the .value_counts() method along with .sort_index() into a dataframe.
two_dice_df = pd.DataFrame(combos_df['Sum Two Dice'].value_counts().sort_index())
# Rename column:
two_dice_df.columns = ['Frequency']
two_dice_df
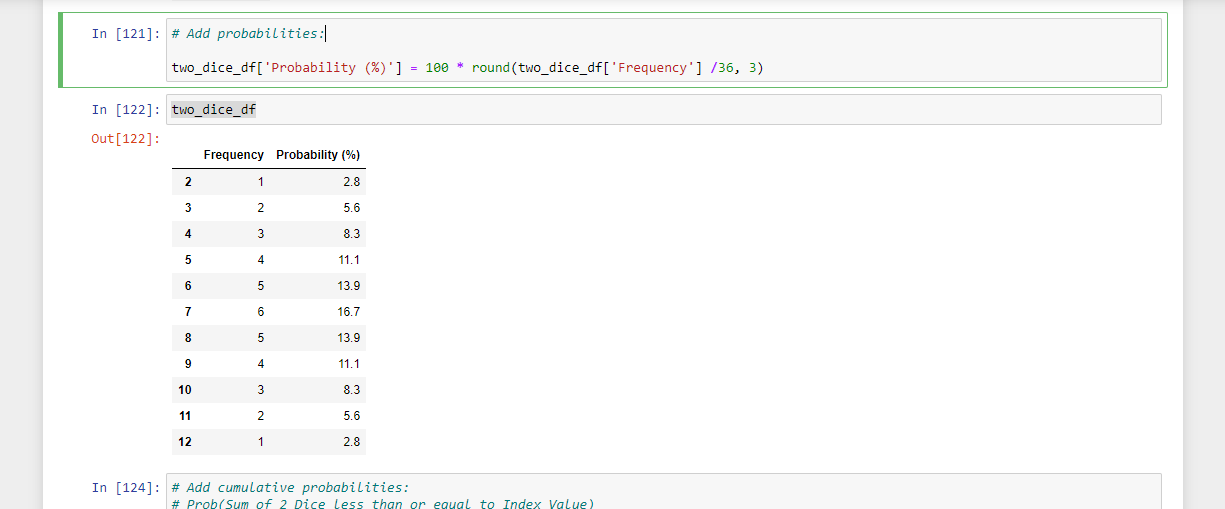
A probabilities column is added next. The probability for a sum of two dice is the frequency divided by a total of 36 orderings.
# Add probabilities:
two_dice_df['Probability (%)'] = 100 * round(two_dice_df['Frequency'] /36, 3)
two_dice_df
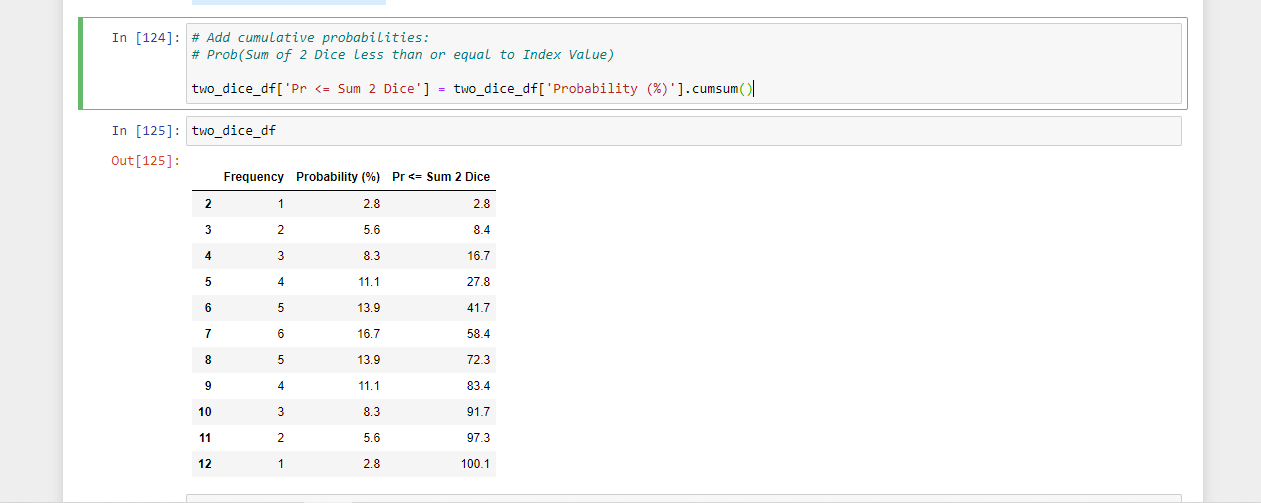
I also add cumulative probabilities with the use of cumsum(). The cumulative probability are all the cases where the Probability of the sum of two dice is less than a value.
# Add cumulative probabilities:
# Prob(Sum of 2 Dice less than or equal to Index Value)
two_dice_df['Pr <= Sum 2 Dice'] = two_dice_df['Probability (%)'].cumsum()
two_dice_df
Some Insights
Here is a nicer table for the sum of two dice. The values are from Python.
| Sum Of Two Dice | Frequency | Probability (%) | Cumulative Probability |
|---|---|---|---|
| 2 | 1 | 2.8 | 2.8 |
| 3 | 2 | 5.6 | 8.4 |
| 4 | 3 | 8.3 | 16.7 |
| 5 | 4 | 11.1 | 27.8 |
| 6 | 5 | 13.9 | 41.7 |
| 7 | 6 | 16.7 | 58.4 |
| 8 | 5 | 13.9 | 72.3 |
| 9 | 4 | 11.1 | 83.4 |
| 10 | 3 | 8.3 | 91.7 |
| 11 | 2 | 5.6 | 97.3 |
| 12 | 1 | 2.8 | 100.1 |
The cumulative probability for the last row is 100.1. Due to rounding the value came out to 100.1. It should be 100.
Seven is number one as the most likely theoretical probability for the sum of two dice. The chance of two standard six-sided dice adding to seven is 16.7%. Six and eight are the next most likely sums with a percentage of 13.9% each.
Rolling a 2 from 2 dice is very unlikely at 2.8%. Twelve is also very unlikely like rolling a two from 2 dice with a percentage of 2.8%.
Rolling a 9 or under from the 2 dice is 83.4% (from the cumulative probability).

Posted with STEMGeeks