Equilibrio de estructuras con cargas perpendiculares al plano — Parte III
Abordaremos el cálculo de reacciones, en esta ocasión de un sistema más complejo respecto al abordado en las primeras dos partes de esta serie de publicaciones:
•Equilibrio de estructuras con cargas perpendiculares al plano — Parte I
•Equilibrio de estructuras con cargas perpendiculares al plano — Parte II
La idea es poner en práctica la resolución de las incógnitas externas, enfatizando el análisis previo a la realización de cálculos, lo cual suele ser el paso más difícil de asimilar y que además hace una importante diferencia a la hora de resolver ejercicios de cargas perpendiculares al plano.
Ejemplo práctico
En esta ocasión, no se realizarán los cálculos correspondientes obteniendo el valor de las reacciones externas. Para comparar resultados numéricos se puede consultar la bibliografía correspondiente, ya que se trata de un ejercicio resuelto de la obra "Estática para Estructuras" del Prof. Iván Rodríguez.
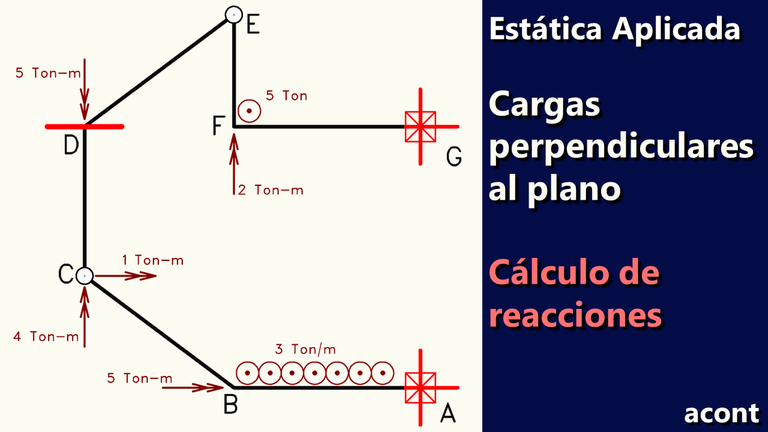
Se trata del siguiente sistema. La imagen animada muestra a su vez las reacciones externas a calcular:
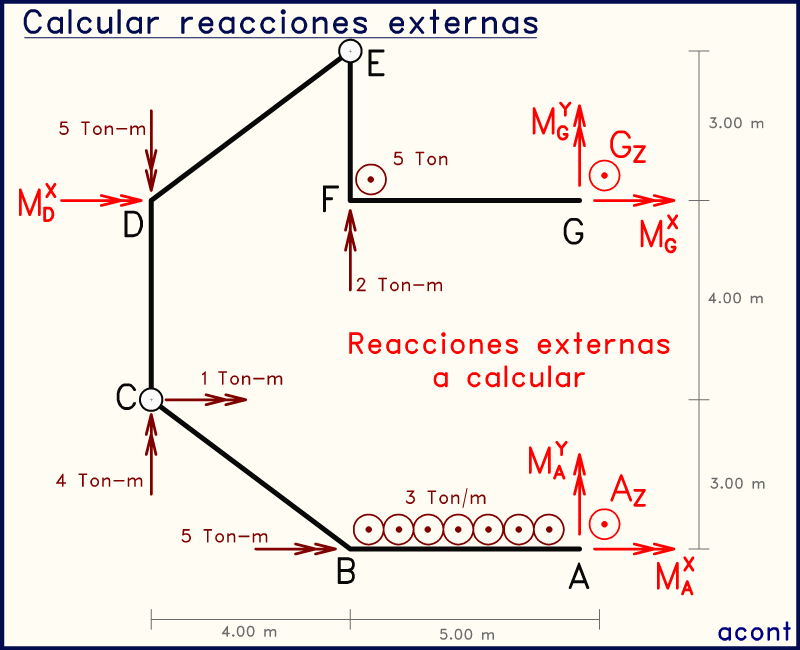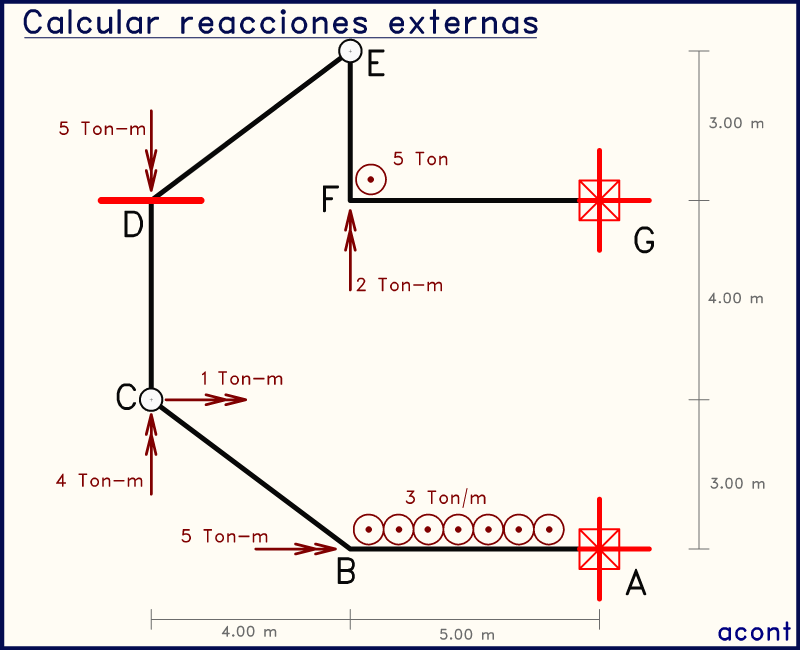
Vínculos externos
En esta ocasión, tenemos dos empotramientos o apoyos totalmente fijos en "A" y "G". Este apoyo totalmente fijo se ha representado a través de la nueva simbología en lugar del empotramiento convencional de sistemas con cargas en su plano, pero ambas formas representan lo mismo: restricción total de movimiento a la chapa que vinculan a tierra.
Según los grados de libertad en el plano X-Y (esto lo vimos en la Parte I), estos vínculos en "A" y "G" brindan tres incógnitas cada uno: fuerza en "Z", momento en "X" y momento en "Y".
Aprovechando para analizar un poco la estabilidad de este sistema, podemos observar que las chapas o cuerpos rígidos "ABC" y "EFG" están restringidas de todo movimiento debido a los apoyos totalmente fijos. Esto daría libertad a la chapa "CDE" para girar alrededor del eje C-E. Es por esto que necesitamos un vínculo externo que restrinja esta posible rotación (imaginar que el punto "D" se mueve perpendicular a la pantalla con "C" y "E" fijos).
De lo anterior, sabemos que para que el sistema sea isostático hace falta un vínculo que anule esta posible rotación. Por ello existe la restricción de rotación alrededor del eje "X" que se encuentra en "D". Este es un vínculo externo de sistemas con cargas perpendiculares que no habíamos tocado en un ejercicio. Su presencia proporciona una incógnita de momento en dicho punto.
Momentos en rótula
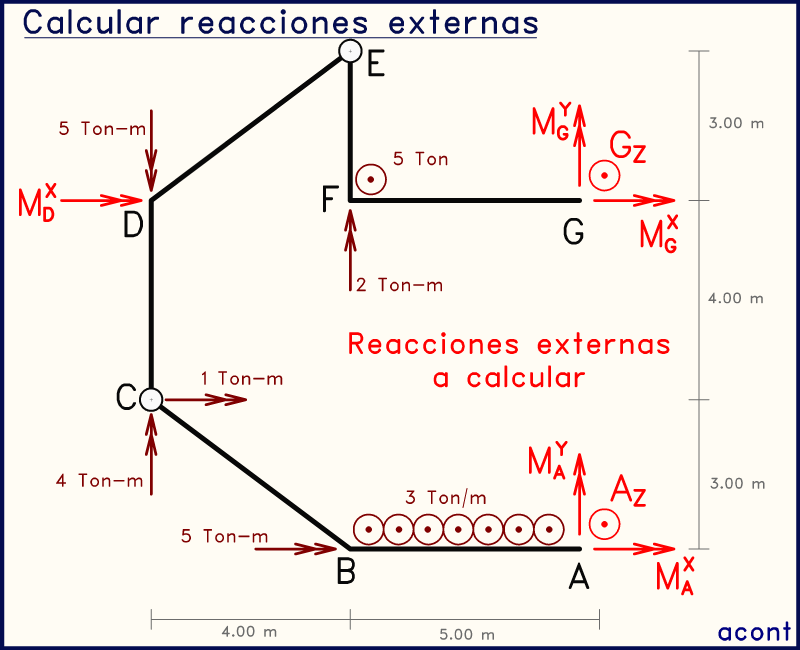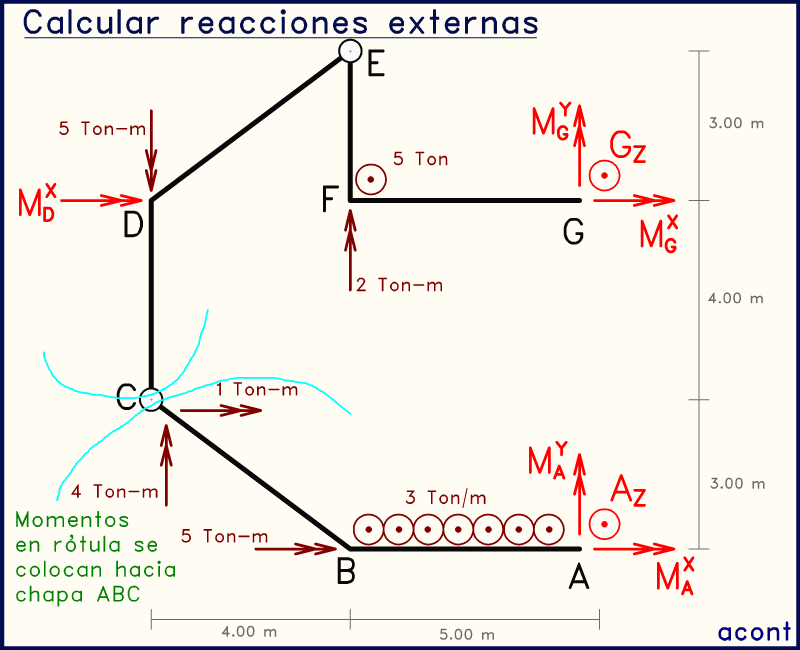
En la imagen anterior, se observa que los momentos que actúan en la rótula "C" son colocados en el extremo de la barra "BC". La razón de esto se explicó en las partes I y II. De un corte en la rótula surgen dos subsistemas ("ABC" y "CDEFG"), de los cuales el de abajo presenta mayor "rigidez" debido al apoyo totalmente fijo y el hecho de no tener ninguna rótula de por medio.
Análisis del sistema
Lo que siempre debemos realizar previo a la realización de cualquier cálculo (en ejercicios más o menos complejos), es analizar con detenimiento el sistema para determinar cual es el camino más efectivo para la resolución de todas las incógnitas externas.
Tenemos en total 7 incógnitas externas. Lo primero que debemos observar es la ubicación de las rótulas, ya que estas nos permiten obtener ecuaciones para la resolución de las incógnitas.
En las animaciones a mostrar, se marcan las rótulas en rosado, las incógnitas de interés están en verde oscuro, y las incógnitas ya determinadas en verde claro. Además, el eje aguamarina discontinuo indica el eje sobre el cual se plantea una sumatoria de momento.
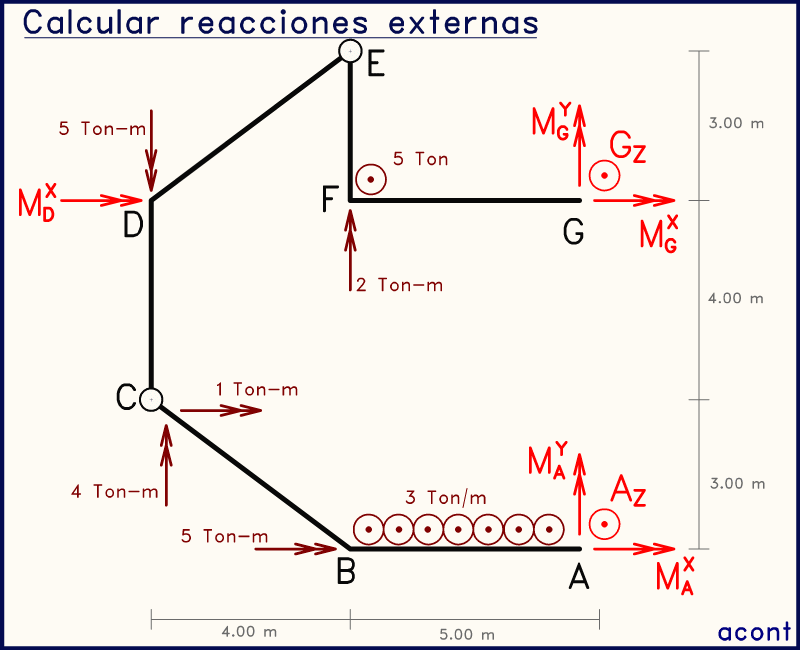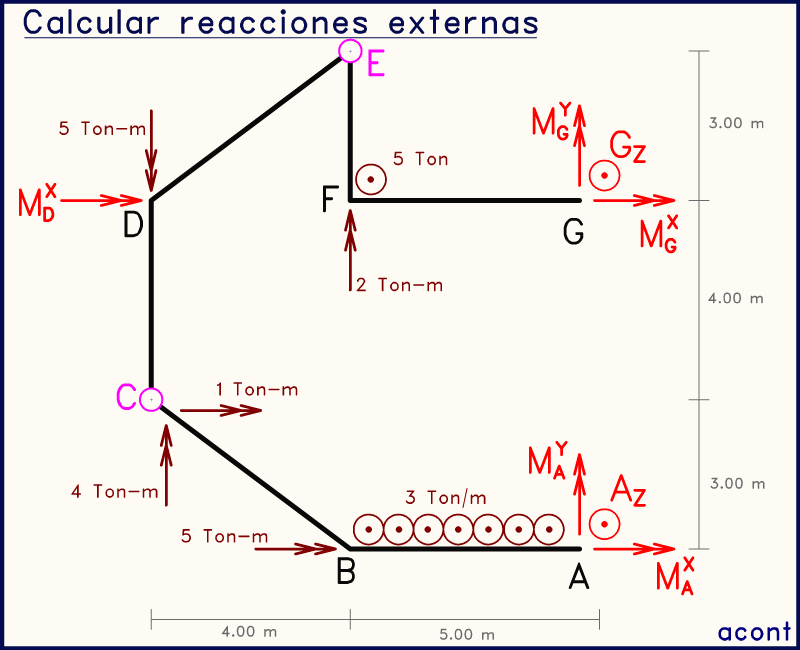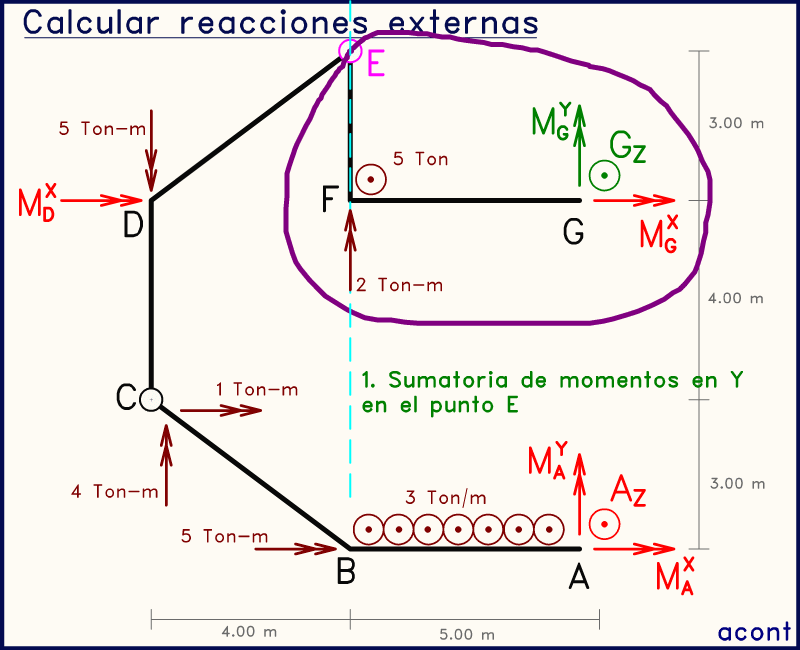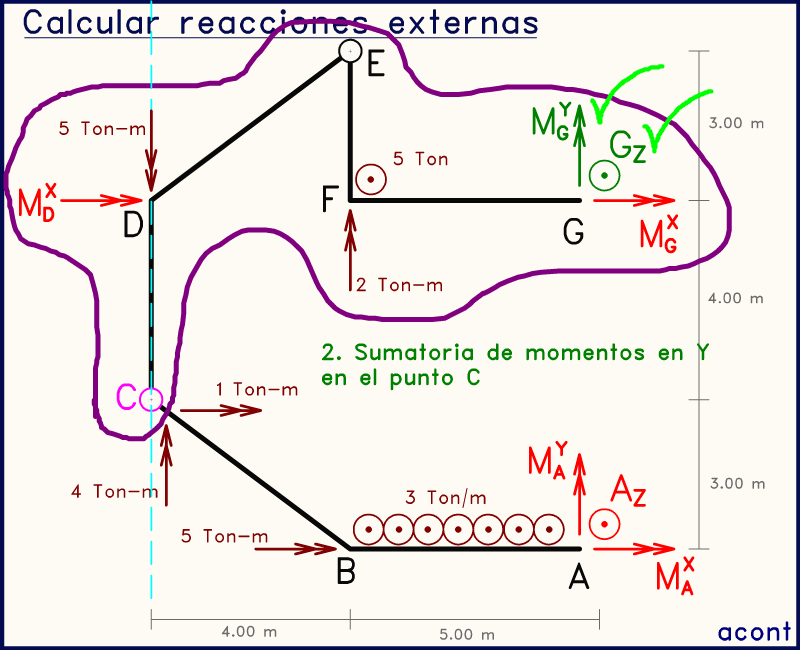
En sistemas con cargas en su plano, dos rótulas seguidas podían servirnos para plantear dos sistemas con dos ecuaciones. En este caso, podemos hacer algo similar solo que es un poco más difícil de evidenciar.
Nos enfocaremos en el subsistema "CDEFG", ignorando lo de abajo. Al existir dos momentos incógnita en dirección "X", se ve que sería más adecuado plantear dos sumatorias de momento en dirección "Y", una en cada rótula, de manera que estos dos momentos incógnita en "X" no aparezcan en las ecuaciones. Obtenemos así dos ecuaciones con dos incógnitas que podemos resolver (MGY y GZ).
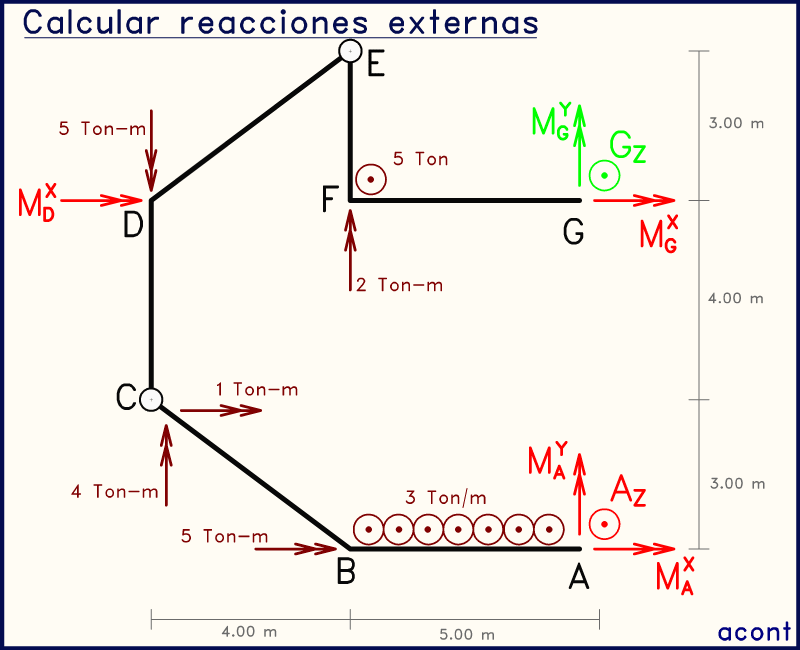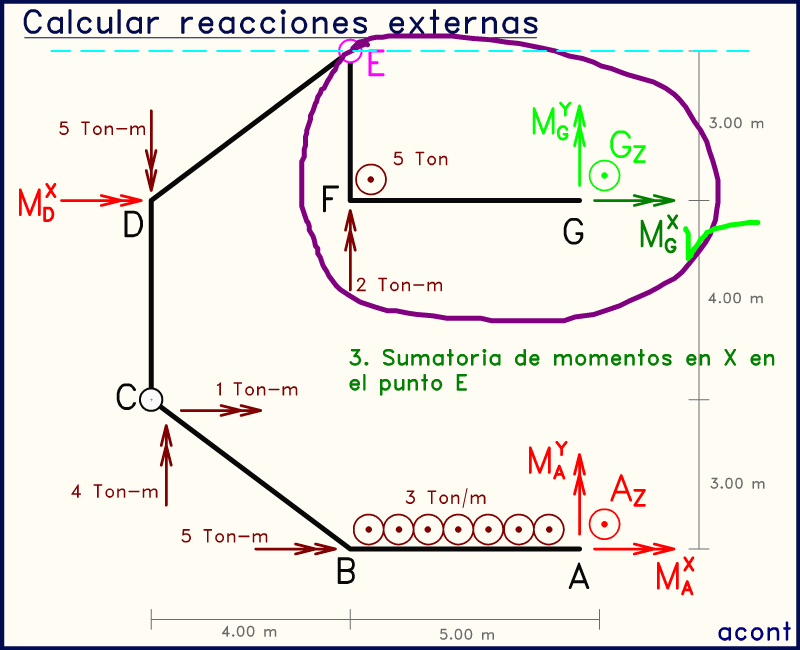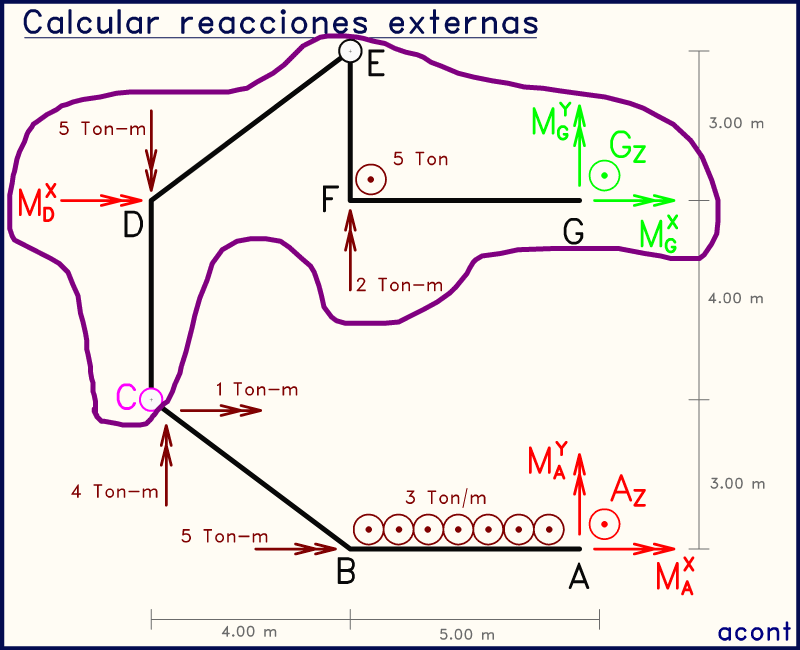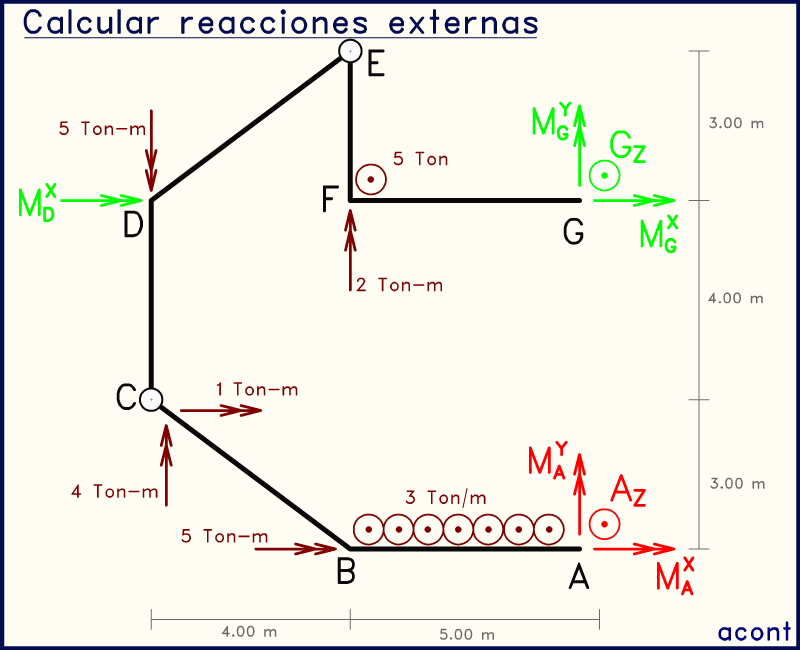
Animación anterior: conociendo MGY y GZ, podemos volver a usar las rótulas pero planteando esta vez sumatorias de momento en dirección "X". Si hacemos esto en el punto "E" para el subsistema "EFG", podemos obtener una ecuación con una sola incógnita que podemos calcular: MGX. Podemos realizar esto de igual manera pero en la rótula "C", de manera que la única incógnita contenida en la ecuación sería MDX.
Las incógnitas ya determinadas de pasos anteriores se marcan en verde claro, de esta manera podemos evidenciar las incógnitas que podemos determinar en el presente paso. Hasta ahora solo no hemos centrado en la estructura de "C" para arriba.
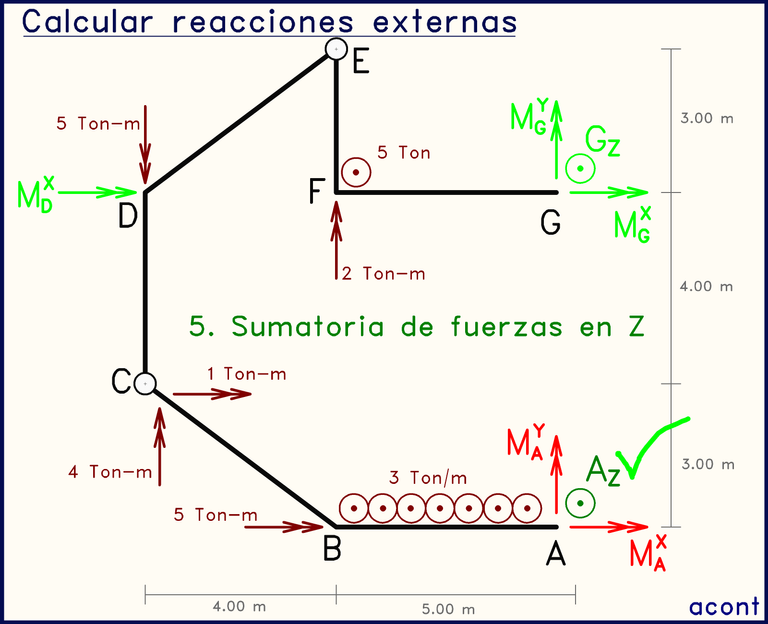
Imagen anterior: en todo el sistema solo tenemos dos incógnitas de fuerza; AZ y GZ. Al conocer ya una de estas dos, podemos fácilmente plantear una sumatoria de fuerzas en dirección "Z" para despejar y calcular la otra.
A diferencia de la sumatoria de momentos, la sumatoria de fuerzas en "Z" se realiza de manera general (en todo el sistema) y no en solo una parte o subsistema del mismo.
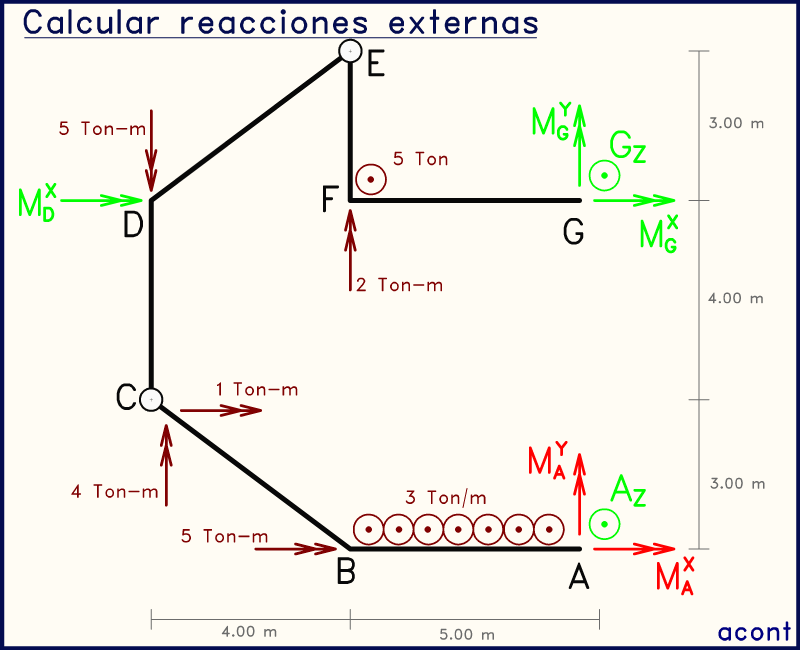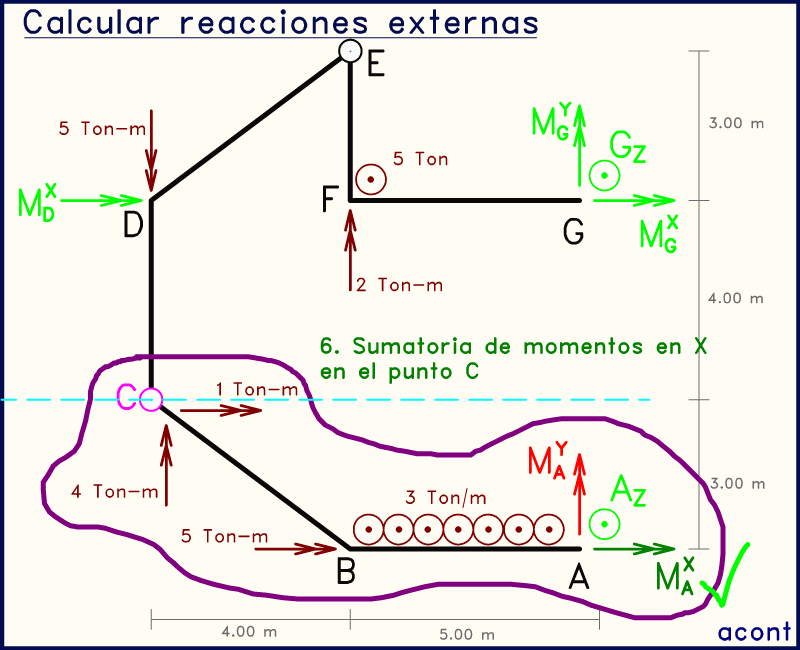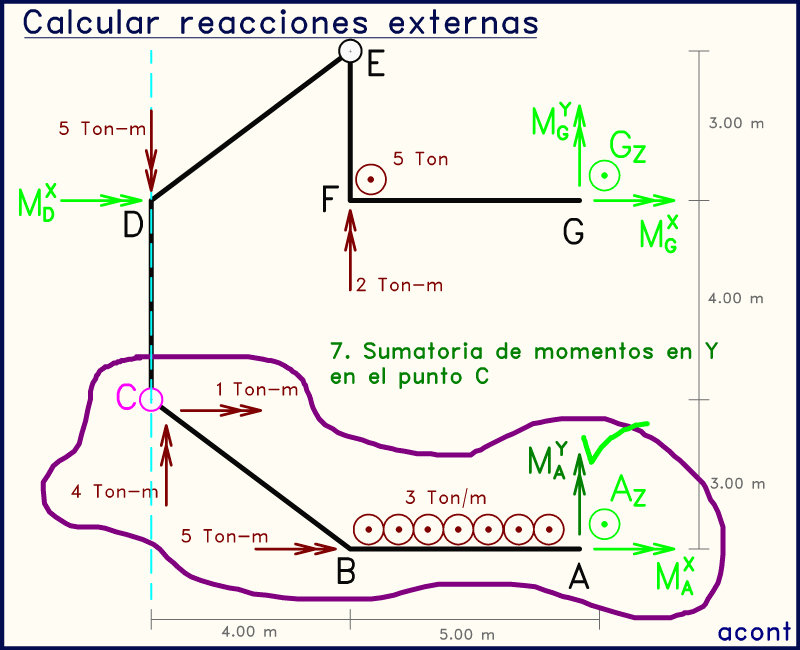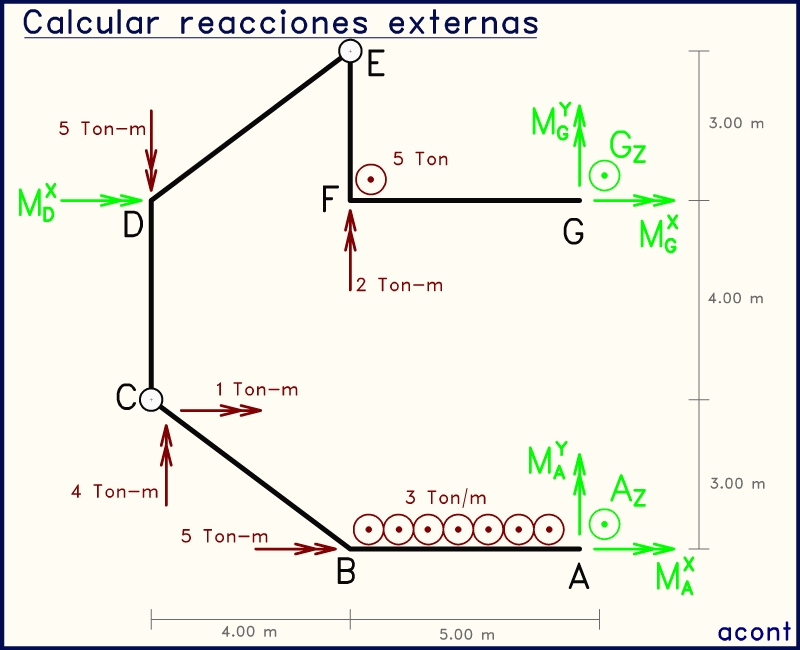
Animación anterior: la rótula en "C" ahora la vamos a utilizar para enfocarnos en el subsistema inferior. Al ya conocer AZ, se nos facilita el cálculo de las dos incógnitas restantes, ya que al plntear por ejemplo una sumatoria de momentos en "X", la incógnita MAY no aparece. La rótula en "C" nos permite plantear sumatorias de momentos tanto en "X" como en "Y". Estas dos ecuaciones contienen cada una una sola incógnita que podemos despejar directamente (MAX y MAY).
De esta manera, hemos hallado un camino para el cálculo de todas las reacciones o incógnitas externas sin plantear ninguna ecuación matemática. Este análisis establece una "hoja de ruta" o orden a seguir para realizar los cálculos, de manera que estos no se conviertan en un dolor de cabeza, ya que plantearlos sin antes hacer esto puede llevar a "callejones sin salida" que hacen perder tiempo al estudiante.
En la próxima publicación abordaremos el despiece de sistemas con cargas perpendiculares al plano, de manera que se ilustre el proceso de hallar las incógnitas internas estableciendo así el equilibrio interno del sistema. Posteriormente, se abordarán los diagramas de solicitaciones de sistemas con cargas perpendiculares al plano.
Aportes de esta publicación
Esta publicación brinda un enfoque en el análisis de sistemas con cargas perpendiculares al plano, para la resolución de reacciones externas de manera efectiva. Se aporta además material útil sobre el tema el cual se encuentra de manera muy limitada en la web y en libros de estática. Se aporta adempas, material que prepara al estudiante en el análisis previo del sistema y su importancia para el desarrollo del ingenio y capacidad analítica, necesaria en la carrera de ingeniería.
Referencias
•Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 202-204, 215-217).Fuente
Imágenes de autoría propia realizadas mediante LibreCAD y PowerPoint. GIFs elaborados mediante Photoscape.
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria conformada por autores de todo el mundo en la que se comparte y apoya la difusión de contenido STEM de calidad entre sus usuarios.
| ¡Gracias por visitar! — ¡Thanks for visiting!  |
Has sido votado por
PROYECTO ENLACE
'Conectando Ideas y Comunidades'
PROYECTO ENLACE es un proyecto de curación de habla hispana enfocado en recompensar contenido de calidad y apoyar autores en su proceso de crecimiento en HIVE.
Creemos y apostamos por el futuro de esta gran plataforma, y estamos muy emocionados de poder hacerla crecer junto a esta comunidad. Así que te invitamos a usar nuestra etiqueta ENLACE y estar atento a todas las actividades que tenemos preparadas y que estaremos publicando en breve.
¿QUIERES AUTOMATIZAR TUS GANANCIAS DE CURACIÓN? SE PARTE DEL PROYECTO ENLACE APOYANDO A NUESTRO TRAIL EN HIVE.VOTE INGRESA AQUÍ PARA CONCOCER LOS DETALLES.
¿QUIERES INVERTIR ENLACE? DESCUBRE COMO HACERLO Y GENERAR INGRESOS DE FORMA SEMANAL MEDIANTE TU DELEGACIÓN DE HP AQUÍ TE EXPLICAMOS COMO.
Te invitamos a participar en nuestro servidor de Discord: https://discord.gg/3S9y7BbWfS
Atentamente
EQUIPO ENLACE 2021
Gracias por el apoyo al equipo de #Enlace
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Gracias a #STEMsocial!
Thanks to STEMsocial project,
https://twitter.com/EspanolStem/status/1365256983729893378