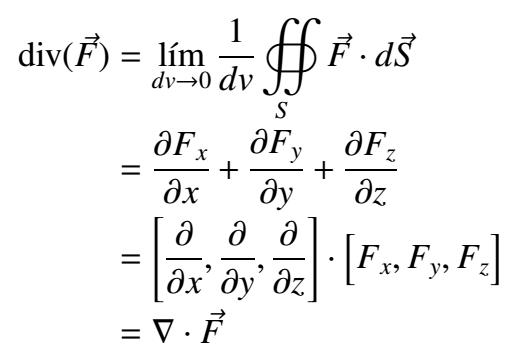The Divergence
In the studies related to the functions of several variables, it is important to understand de differentiation of vector fields, specifically to study their variation into the R³ space. For this, two useful tools are presented, The Rotational and The Divergence, for this work, we are going to study The Divergence.
The Divergence studies the variation of the flux lines of the vector field. We can say that it derives along, or over these lines. If we want to make this study we have to understand how these lines go through the infinitesimals surfaces perpendiculars to them. In other words, The Divergence requires the vector field's flux to differentiate it, but it makes this study for each one of these lines (or vectors) at the same time, this implied to go one by one and taking each time a smaller surface until it fitted to only one line of flux (this implied to take the limit that makes tends the section of those surfaces to zero), then to take the next line, repeat the calculation and summing with the first result, then to take another line and summing the three results, and so on. One way to do all this work is to take a closed general surface that contains all the lines, to compute the flux of the vector field through this section, and to take the limit of the volume closed by the surface to cero.
With these ideas, we get the following math expression for The Divergence

We want to find a straightforward operational expression to eval The Divergence of any vector field, following the expression above the idea is to submerge a closed surface (that can be placed at any coordinates in ℝ³), that enclosed an infinitesimal volume dv=dx dy dz (we will work with cartesian coordinates) into a vector field F=F(x,y,z). The components of the vector field can be any scalars fields that depend on the variables x,y or z.
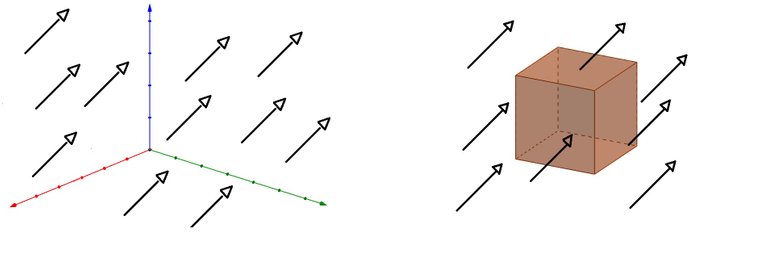
If the vector field is decompounded in î, ĵ, k̂ and we make that each component goes through the surface's section that it corresponds, it will be possible to study each component independently and it will be easier to make the math.
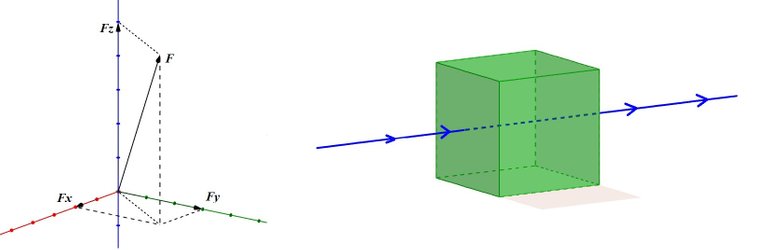
By this way we can deal with F as Fx, Fy, Fz and make the studies of each component separately, when the field is restringed to move only on one fixed dimension (x,y or z) and also goes through a fixed point at the cube the outcome is that two of its variables stay constant, and the remainder one only can vary over the line that it correspond.
Henceforth the aim is to calculate the flux F through the surface component by component, each component implies to take two faces in the cube, let's begin for Fy
What we want to do implies to consider the next symmetry.
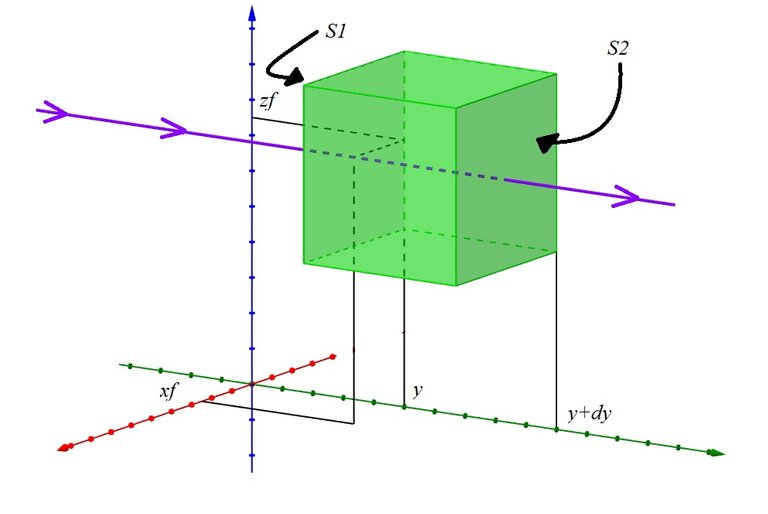
We are going to use F=Fy=(xf, y, zf). Where xf and zf are the variables of the vector field that we fix in a constant value to we stay in one line over the field.
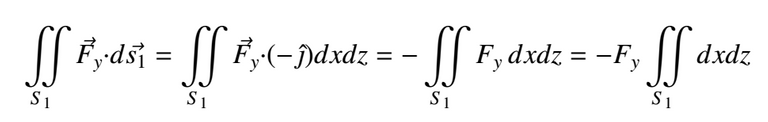
The integral's outcome is the section of S1. However, as such section is part of the infinitesimal surface, then
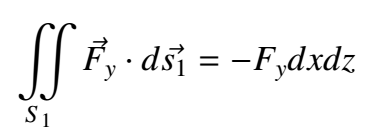
Confusion can arise in the fourth step of the solution, where we took Fy out of the integral as a constant, when it has been repeated that it is dependent on x and z, to understand this we have to rememmber that we fixed the values of such variables for this calculation, but then, the next question can arise ¿In the result, can Fy depend on x and z? The answer is YES, and this answer goes further than the calculation. It has to do with where we are taking the integral, the differential cubic surface CAN BE AT ANY PLACE IN THE SPACE, this means that if we move the cube a little in either x or z and we repeat the calculation, we would have fixed other x and other z, besides to vary such x and z on the integral would imply to take into account other flux lines that go through S1, in this case, we only have to consider one, later we will see why.
Continuing whit the next surface.
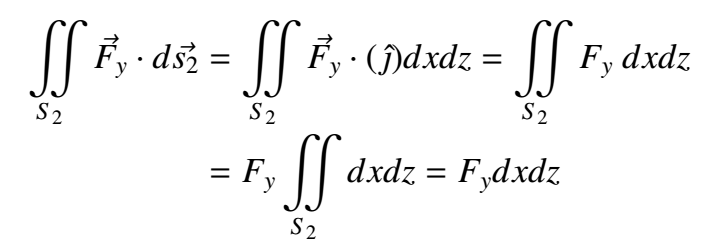
But in this case Fy = Fy(x,y+dy,z) ¿What does this mean? The aim is to find a more simple expression for our calculations. As we are over the flux's line where x,z=Ctes we can approximate the expression by a Taylor polynomial in y. Remember that we are at the surface S2 for y=y+dy.
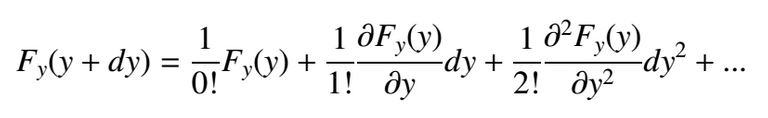
Those terms farther the first derivative are neglected because of the fact that the squared of a differential amount as dy is in the practice nearly to zero. Therefore, going back to the integral

Adding the fluxes in both S1 and S2
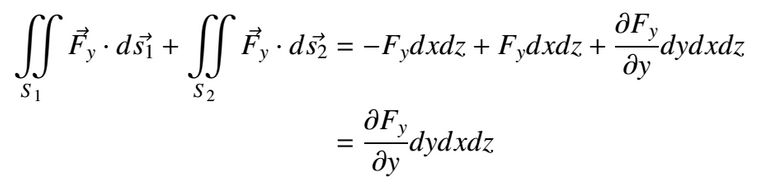
If we divide this result for the cube's volume, we will get how much of the flux there is for the surfaces S1 and S2 for volume, if we also tend the volume to zero as the definition for the divergence states, we will get
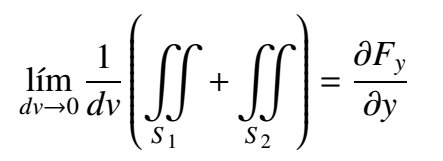
The conclusion is that the "differential of flux" on the component y of F through an infinitesimal volume is equal to take the component of the field y and derive it partially respect to y.
But we still have four surfaces that would throw two further results (similars) which we have to add to the already found one, we can do this thanks to the superposition principle for field fluxes over a surface.