La desigualdad entre expresiones algebraicas
Inecuaciones
La desigualdad entre expresiones algebraicasYa estamos acostumbrados a resolver las funciones como una relación entre las variables a través de una Igualdad, donde se dan valores de entrada y calculamos su imagen representada por el Rango de la función.
En esta publicación veremos que existen formas de representar una Desigualdad algebraica, donde debemos calcular los valores de las variables que satisfagan esa desigualdad. Para tratar este tema, los matemáticos hacen uso de los operadores: mayor que >, mayor o igual que ≥, menor que < y menor o igual que ≤

2m + 4 = 3m, es un típico ejemplo de una igualdad algebraica, donde la variable m se determina así:2m + 4 = 3m
2m − 3m = −4
−m = −4
m = 4
Esta relación de igualdad se cumple para un valor específico y único de m = 4, está relacionado con la solución de la expresión matemática. También existen relaciones de desigualdad donde se requiere encontrar los valores de la variable incógnita que satisfaga la desigualdad y son llamadas Inecuaciones.

La relación de desigualdad no se cumple para valores de m ≥ 4, por lo general se resuelve de forma parecida a la expresión algebraica de una igualdad, despejando la variable m y conservando el operador mayor que (>), así:
2m − 3m > −4
−m > −4
m < 4
con la notación de intervalos abiertos en ambos extremos: (−∞, 4)
Las mismas operaciones que aplicamos en las ecuaciones, con la excepción que si en las inecuaciones se multiplica o divida entre un número negativo, entonces debemos cambiar el sentido del operador, por lo que la inecuación también cambia de signo. Esto fue lo que hice en el último paso del ejemplo anterior!
INECUACIONES con solución gráfica
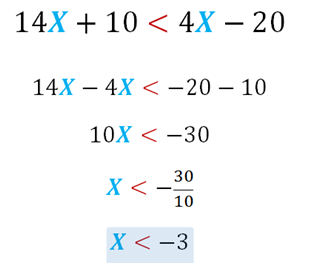
Es un ejemplo de inecuación lineal, porque el exponente de la variable X es de orden 1. El miembro de la izquierda será menor que el miembro de la derecha para valores de X menores que −3, con la notación de intervalos abiertos en ambos extremos: (−∞, −3)
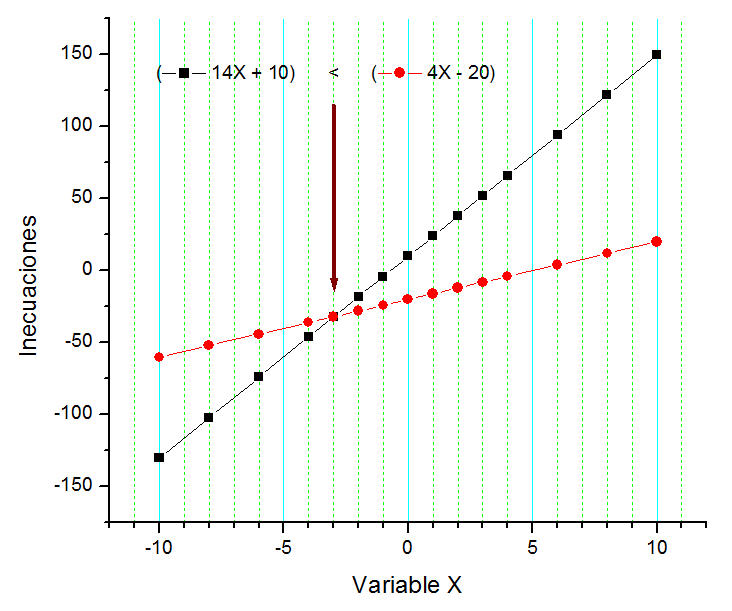
En la mayoría de los casos las inecuaciones son condicionales y están sujetas a ciertos rangos de valores de la variable, y nos aportan información sobre las expresiones algebraicas y sus fronteras comunes.
Apoyo bibliográfico y fuente de imágenes
Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
- Imagen de Alexas_Fotos: Portada de inecuaciones
- Wikipedia: Inecuación
- Ecured: Inecuaciones cuadráticas
las variables de una igualdad o desigualdad,
para hallar la solución de la ecuación o inecuación
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.