La ecuación de la recta en el espacio – Un enfoque didáctico
La ecuación de la recta en el espacio – Un enfoque didáctico
1. Introducción
En mi experiencia como docente sé que la enseñanza de la matemática muchas veces se hace pesada y demasiado abstracta para algunos estudiantes. Muchos de ellos incluso tienen un excelente dominio para realizar operaciones matemáticas complejas, sin embargo, esa habilidad operativa no es suficiente y que se necesita una comprensión de lo que se está haciendo. Un ejemplo de esto es la ecuación de la recta en el espacio.
El estudio de la geometría euclidiana en el espacio en nuestro sistema educativo es bastante deficiente, de hecho, a nivel universitario cuando se topan con la matemática tridimensional los estudiantes se limitan a la parte operativa, sacar cuentas, pero se olvidan totalmente de la comprensión y se les dificulta poder ver o imaginarse físicamente en el espacio lo que significa una expresión determinada de tres variables.
Un caso típico de esto es la ecuación de la recta en el espacio, también llamada la ecuación simétrica cuya expresión es la siguiente:
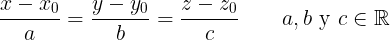
Imaginarse una recta en el espacio es algo sumamente fácil, a un niño se le puede dar un ejemplo de esto por medio de una cuerda, un fino tubo o una vara, o cualquier cosa fina y firme en un espacio determinado, ya sea el salón de clases o cualquier otro lugar, y de seguro sabrá comprender lo que es una aproximación de un objeto abstracto en el espacio y esto lo ayudará a entender su significado.
Sin embargo, al ver la ecuación de arriba un estudiante universitario no puede visualizar por completo el significado de esta y mucho menos imaginarse algo más allá de la simple recta que visualiza un niño.
Por esta razón he querido hacer una explicación por medio de un ejemplo didáctico y sencillo que pueda un estudiante universitario entender lo que es una recta en el espacio y el significado de su ecuación simétrica.
2. Procedimiento y construcción.
Antes que nada es importante también explicar por medio de recursos didácticos, lo que es el espacio euclidiano para esto haré referencia a un artículo publicado por mí en este blog hace algún tiempo Ver artículo. A continuación extraigo lo expuesto en esa entrega de entonces:
2.2.2. El espacio euclidiano.
Para representar el espacio euclidiano se construyó en madera una especie de caja cúbica abierta en la que se muestran los ocho octantes del espacio tridimensional, cada octante se pintó de un color diferente y se tomaba el octante positivo, es decir, con los ejes "x", "y" y "z" positivos, arbitrariamente. Este diseño ayudó enormemente al estudiante a identificar los planos en el espacio, es decir los planos x = 0, y = 0 y z = 0, del sistema de coordenadas cartesiano, ver Fig. 3.

2.2.3. Los ejes coordenados.
Los tres ejes coordenados cartesianos se construyeron con cabillas de acero, cada cabilla representa un eje coordenado los cuales se pintaron de diferentes colores, verde el eje x, azul el eje y y rojo el eje z, los tres ejes se cruzaron en un punto en común el cual se unió mediante soldadura, cada eje tiene su lado positivo y negativo, al final de cada eje se colocó una flecha que indica su dirección y se pintó de color blanco, ver Fig. 4. Este modelo de los ejes coordenados junto con el del espacio euclidiano ayudó enormemente al estudiante a poder ubicar los vectores en el espacio, así como la ubicación de puntos y coordenadas en tres dimensiones.

Ahora procedamos a nuestro nuevo objetivo. Comencemos con la construcción de un octante positivo x, y y z.
2.1. Construcción del octantante x, y, z.
Para construir el octante tomamos una caja de cartón y le quitamos dos de sus lados (Ver Figura 1)

Figura 1. Caja de cartón para hacer el octante x,y,z positivo.
Luego forramos con papel blanco los lados o paredes de la caja para luego construir las escalas (Ver Figura 2).

Figura 2. Forrado de blanco de las paredes de la caja
Las paredes de la caja representarán los planos xy, xz y yz; luego precedemos a dibujar o marcar la escala correspondiente a cada eje coordenado (Ver Figura 3).

Figura 3. Representación de los planos correspondientes al octante y dibujo de la escala en centímetros.
2.2. Construcción de la cuerda en el espacio pasando por el octante x,y, z.
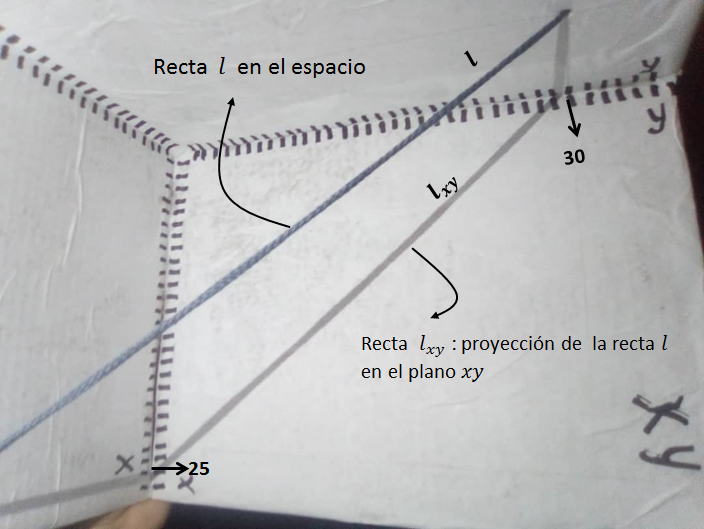
A continuación se precede a pasar una cuerda fina o cordón para representar la recta l en el espacio. Para esto hacemos dos agujeros en los planos “xz” y “yz” es decir la recta cortará estos dos planos, es importante señalar y recordar que una línea recta es infinita, es decir, ella se prolonga a ambos lados indefinidamente. Obviamente los agujeros se pueden hacer en cualquier plano y en cualquier parte de los mismos. Ver Figuras 4 y 5.

Figura 4. Agujeros en los planos “xz” y “yz” por donde pasará la recta

Figura 5. Uso del cordón o cuerda que pasa por los planos escogidos. La cuerda representa parte de la recta
 .
. 2.3. Proyección de la recta en el espacio sobre los planos del octante.
Teniendo la recta en el espacio procedemos ahora a proyectarla en los planos del octante, para hacer esto simplemente buscamos un lugar totalmente a oscuras oscuro y con una linterna —para este proyecto yo usé la linterna de mi celular— iluminamos la recta o cuerda para que se proyecte en cada uno de los planos, es decir vamos a obtener la sombra de la cuerda en los planos xy, xz y yz. Es importante tener presente que esta proyecciones las debemos hacer tratando que el haz de luz de la linterna llegue de forma perpendicular a los planos respectivos, ya que de lo contrario obtendremos sombras que no corresponden a nuestro sistema de referencia u octante escogido.
2.3.1 Proyección sobre el plano xy.
Si observamos la Figura 6a. podemos ver que tenemos la recta en el plano xy , llamemos esta recta 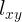 que no es más que la sombra o proyección de la recta
que no es más que la sombra o proyección de la recta 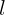 sobre el plano xy. También podemos obtener los puntos de corte con los ejes "x" y "y" que son
sobre el plano xy. También podemos obtener los puntos de corte con los ejes "x" y "y" que son 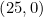 y
y  respectivamente, esto nos permitirá hallar la ecuación de esta recta
respectivamente, esto nos permitirá hallar la ecuación de esta recta 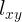 . (Ver Figura 6a).
. (Ver Figura 6a).
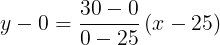
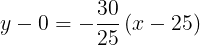
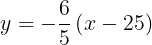
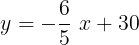
Esta es la ecuación de la recta en el plano xy, es decir la ecuación de la recta
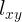 . Escribamos esto de la siguiente forma:
. Escribamos esto de la siguiente forma:
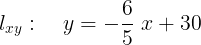
En la Figura 6b hemos dibujado esta recta tomando solo el plano xy.
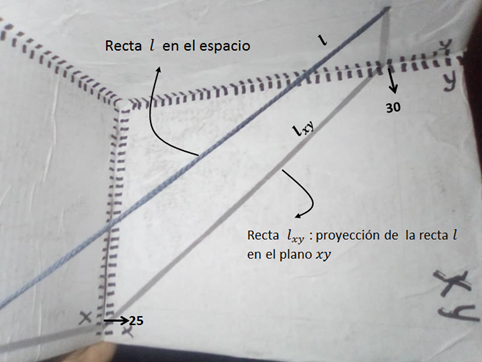
Figura 6a. Proyección (sombra de la cuerda) de la recta en el plano xy.
Figura 6b. Gráfica de la recta
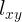
2.3.2 Proyección sobre el plano xz.
Procedemos de igual manera que la sección anterior 2.3.1 y obtenemos la ecuación de la recta proyectada en el plano xz.
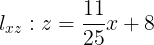
Las imágenes obtenidas y el dibujo de la gráfica la podemos observar en las siguientes figuras 7a y 7b.
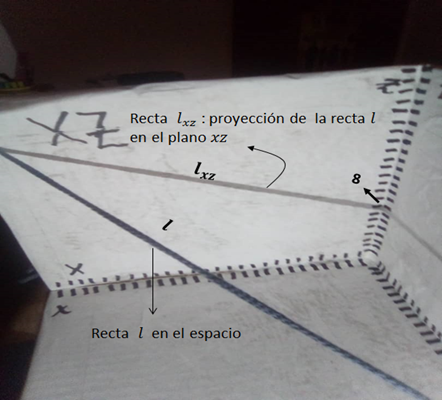
Figura 7a. Proyección (sombra de la cuerda) de la recta en el plano xz.
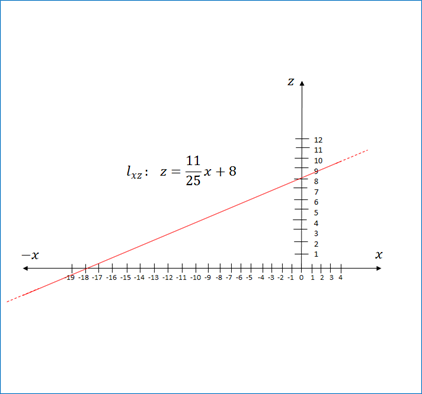
Figura 7b. Grafica de la recta
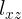
Como podemos observar en la figura 7b la recta corta al eje z en 8, pero corta al eje x en -18.18, esto no puede apreciarse en el octante x,y,z que hemos construido ya que el eje x es positivo y la recta lo corta en –x. Esto se puede apreciar bien en proyección de nuestra recta 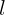 sobre el plano xz. Ver sombra de la cuerda en la figura 7b.
sobre el plano xz. Ver sombra de la cuerda en la figura 7b.
2.3.3 Proyección sobre el plano yz.
Procedemos de igual manera que la secciones anteriores 2.3.1 o 2.3.2, de esta forma y obtenemos la ecuación de la recta proyectada en el plano yz.
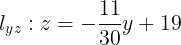
Las imágenes obtenidas y el dibujo de la gráfica la podemos observar en las siguientes figuras 8a y 8b.
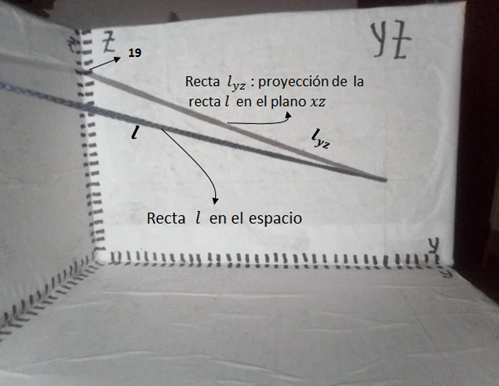
Figura 8a. Proyección (sombra de la cuerda) de la recta en el plano yz.
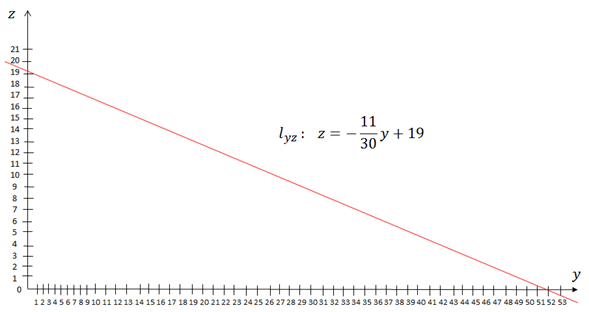
Figura 8b. Grafica de la recta
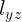
Como podemos observar en la figura 8b la recta corta al eje y en 51.8, este número está fuera de la escala de nuestro octantante lo que se puede apreciar en la figura 8a.
3. Deducción de la ecuación de la recta en el espacio. Ecuación simétrica de la recta.
Hemos obtenido y apreciado físicamente las ecuaciones de las rectas en los planos de nuestro octante x,y,z. Enumeremos estas rectas a continuación
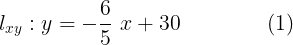
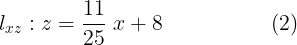
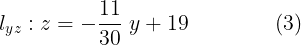
Usemos nuestro modelo del octante para deducir la ecuación de la recta en el espacio. Para esto demos un paso más desafiante y construyamos ahora un vector 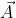 que sea paralelo a la recta
que sea paralelo a la recta  , para esto tomamos los puntos
, para esto tomamos los puntos  y
y  que cortan los planos xz y yz de nuestro octantante (Ver figura 9)
que cortan los planos xz y yz de nuestro octantante (Ver figura 9)
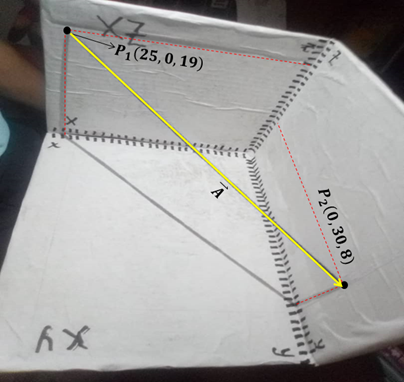
Figura 9. Vector
 paralelo a la recta
paralelo a la recta 
Podemos observar que el vector que hemos construido no solo es paralelo a la recta sino también que pertenece a ella, es decir 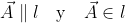 .
.
Hallemos las componentes del vector 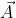
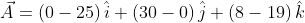
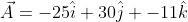
Ahora construyamos otro vector 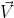 que también sea paralelo y pertenezca a
que también sea paralelo y pertenezca a 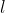 pero cuya magnitud no conocemos, hagamos coincidir la punta del vector
pero cuya magnitud no conocemos, hagamos coincidir la punta del vector 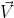 con la del vector
con la del vector
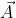 en el punto
en el punto 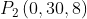 de la recta
de la recta  . Tomemos un punto
. Tomemos un punto 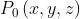 cualquiera que también pertenezca a la recta l. (Ver figura 10)
cualquiera que también pertenezca a la recta l. (Ver figura 10)
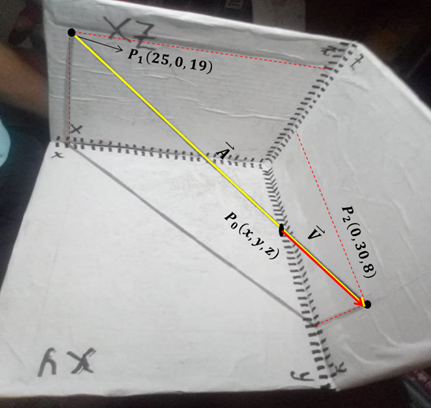
Figura 10. Vector
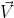 paralelo a la recta
paralelo a la recta 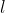
Hallemos ahora las componentes del vector 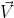
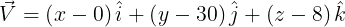
Sabemos que si multiplicamos por un escalar 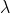 (un número real) al vector
(un número real) al vector 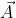 podemos obtener un vector de magnitud y dirección igual al vector
podemos obtener un vector de magnitud y dirección igual al vector 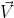 es decir
es decir
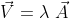
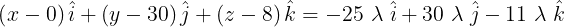
Por lo tranto

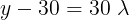
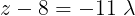
Al despejar 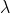 tenemos
tenemos
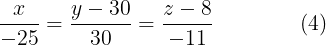
Esta es la conocida ecuación simétrica de la recta en el espacio, la pregunta es ¿qué significa esa ecuación? Si tomamos las igualdades de la ecuación (4) podemos deducir lo siguiente
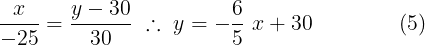
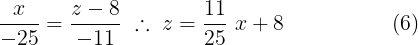
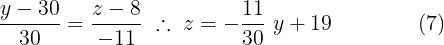
Como podemos ver (5) = (1) que es la ecuación de la recta 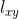 , (6) = (2) que es la ecuación de la recta
, (6) = (2) que es la ecuación de la recta 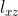 y (7) = (3) que es la ecuación de la recta
y (7) = (3) que es la ecuación de la recta 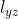 .
.
De tal manera que la ecuación simétrica expresa las ecuaciones de las rectas que son proyecciones sobre los planos xy, xz y yz.
Podemos ahora tomar un punto cualquiera de la recta l escogiendo un punto al azar en la cuerda de nuestro modelo y midiendo las coordenadas de dicho punto. Ver figuras 11 y 12.

Figura 11. Ubicación de un punto en el espacio perteneciente a la recta
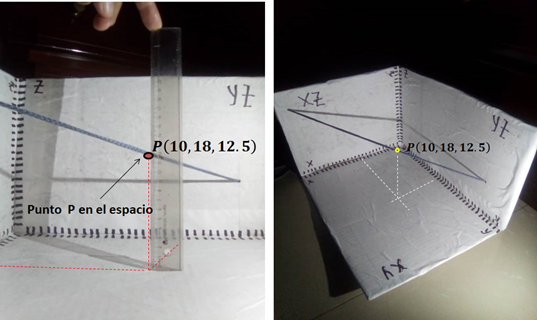
Figura 12. Coordenadas del punto P en nuestro octante
Sustituyamos este punto en la ecuación simétrica (4) que representa la recta 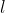
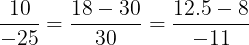
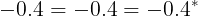
 El valor real calculado de
El valor real calculado de 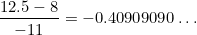 esto es debido a la imprecisión de nuestra escala hecha a mano.
esto es debido a la imprecisión de nuestra escala hecha a mano.
4. Conclusión
La utilización de modelos didácticos para la explicación de las matemáticas puede ayudar enormemente a la comprensión de sus conceptos, principios y leyes.
El modelo que hemos expuesto en este trabajo nos muestra de una forma sencilla y didáctica uno de los conceptos de la geometría euclidiana, el de una recta en el espacio. Esto se ha hecho tan solo con una caja y una cuerda que nos ha permitido abordar temas como el espacio, la ecuación de la recta, proyecciones de rectas en el plano y la utilización de vectores para hallar ecuaciones de rectas.
Creo que esta forma de enseñanza lleva al estudiante a comprender mucho mejor los objetos abstractos de la matemática además de ayudarlos a desarrollar su creatividad y entendimiento en temas que muchas veces se hacen tediosos y poco comprensibles por su complejidad.
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Hive Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Te informamos que el PROYECTO ENTROPÍA ha puesto en marcha un nuevo servicio, la Creación de cuentas nuevas de Hive, para más información puedes visitar este enlace.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Excelente.
Felicitaciones @rnunez09, no es mi área fuerte o de formación, pero sin duda, esta entrega realmente tiene un enfoque muy didáctico, el uso de imágenes obtenidas al construir ejemplos en 3D con cartón y papel, desde lo didáctico es el elemento de mayor relevancia.
Muchísimas Gracias por tu comentario.
Excelente artículo, explicas de manera muy didáctica el estudio de la ecuación de la recta y su representación en 2D y 3D, sin duda un trabajo de calidad. Lo invito a leer mi publicación sobre Geometría Descriptiva: http://hive.blog/steemstem/@acont/geometr-a-descriptiv-1579989123 esa es la parte I. Saludos.
Muchísimas Gracias por tu comentario. Por supuesto que leeré tu publicación.
Gracias nuevamente.
Gracias por compartir tus extraordinarios conocimientos en la plataforma Hive.blog en especial con la comunidad de Stem-espanol, profesionales como tú son ejemplos a seguir ya que ayudan a mejorar notablemente la comprensión abstracta de las operaciones matemáticas realizadas por los estudiantes, logrando así la consolidación de dicho aprendizaje. Un saludo fraterno.
No sabes cuanto agradezco tus comentarios, esto me motiva a seguir tratando de hacer artículos que realmente ayuden a la divulgación y entendimieto de las ciencias, en este caso particular de las matemáticas.
Realmente es como tu dices, esta plataforma ayuda mucho a dar a conocer formas nuevas y creativas de aprendizaje de conceptos abstractos.
Una vez más, muchísimas gracias.
Saludos amigo @rnunez09.
Excelente material el que nos presentas.
Me has dado una idea maravillosa para mis clases de cálculo III, realmente la dificultad más grande que tengo para las gráficas de superficies cuádricas como paraboloide elíptico, paraboloide hiperbólico y los hiperboloides tanto el de una hoja como el de dos hojas es que su gráfica no es tan comprensible cuando se dibuja en el pizarrón.
Pero tomando el ejemplo de la construcción del sistema tridimensional (octante X,Y,Z) que realizaste, puedo de igual manera realizar toda el algebra involucrada para las gráficas, pero al momento de graficar de seguro que si logro construir el octante que aquí se explica de seguro que las gráficas tridimensionales serán mas entendidas.
Saludos y gracias por compartir tus conocimientos y experiencias de trabajo con la comunidad de stem-espanol.