Sistema de ecuaciones lineales y métodos de resolución: Problema de aplicación
Según el portal web de PDVSA. En Venezuela, el 60% del gas licuado de petróleo se comercializa en tanques de 10 kg, 18 kg y 43 kg. El estado por medio de su compañía es responsable de la distribución a través de su subsidiaria PDVSA gas comunal. Corporación creada para establecer un vínculo directo con las comunidades a través de sus líderes. Cada comunidad debe aprobar una contabilidad mensual del total de tanques vendidos, el número de tanques vendidos por presentación y el dinero total recaudado en ventas. Solo entonces se puede agregar la comunidad a una lista de espera y luego aprobar su envío. No es una razón para nuestro trabajo, Solo señalar que este proyecto no ha tenido éxito, es decir, no ha podido satisfacer la demanda de gas doméstico que existe en la población. Una comunidad desea organizar la contabilidad de la venta de tanques de gas licuado. Para ello cuenta con la siguiente información: El mes pasado obtuvimos un total de 498 mil bs en ventas de tanques. Se vendieron un total de 30 tanques. Se sabe que solo se vendieron tanques de 10 kg y 18 kg. La persona a cargo no tomó nota de cuántos tanques fueron facturados de cada presentación. La comunidad a través de sus líderes necesita el registro detallado de esa contabilidad para procesar la próxima solicitud a las oficinas de PDVSA gas comunal. De forma intuitiva. Un modelo matemático es un procedimiento en el cual las situaciones que ocurren a nuestro alrededor se transforman mediante el lenguaje algebraico. Es decir, convertir los datos en sistemas a estudiar para dar respuesta, a través de métodos analíticos para aportar las ideas con sus posibles soluciones.. Por otro lado, nos muestra cómo actuar en cada situación particular desde su generalización. Teniendo en cuenta que cada situación puede llevarnos a nuevos modelos matemáticos de diferente naturaleza. 1. Traducción algebraica de los datos 2. Planteamientos del sistema 3. Resolución del sistema Procederemos a colocar las diferentes variables en un cuadro para visualizar cada uno de los datos y tener idea más clara de la situación. Procederemos a identificarlas con una letra, lo cual facilitará el trabajo. X = número de tanques vendidos de 10 kg Sabemos que el número total de tanques vendidos fue 30, por tanto, planteamos la siguiente ecuación:
Creditos: Gerd Altmann in pixabay
Introducción
Problema (supuesto)
¿Podemos ayudar a esta comunidad?
Modelo matemático
Como resultado, podemos resumir este método en tres pasos:Luego, abordaremos el problema utilizando este método.
1. Traducción algebraica de los datos
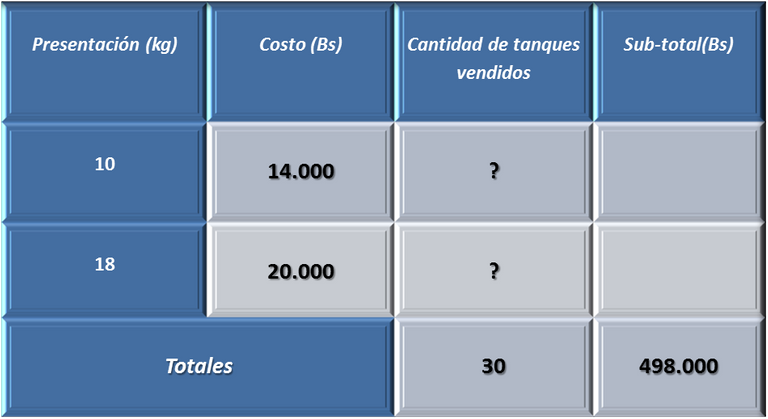
En el cuadro, nuestro problema cuenta con dos incógnitas, en este caso, la cantidad de tanques vendidos de 10 kg y la cantidad de tanques vendidos de 18 kg.
Y = número de tanques vendidos de 18 kg
Por otro lado, sabemos que el costo de cada tanque de gas de 10 kg y 18 kg por presentación es de 14000 Bs y 20000 Bs, respectivamente. Asimismo, el monto total de la venta es de 498000 Bs. Entonces podemos plantear la ecuación:
2. Planteamientos del sistema
A continuación, podemos observar que nuestro problema particular produce un sistema de ecuaciones de dos ecuaciones y dos incógnitas. Se representa de la siguiente manera:
En casos particulares, se pueden identificar posibles simplificaciones de las ecuaciones, por lo tanto, es conveniente realizarlas para evitar complicaciones al resolver el sistema.
3. Resolución del sistema
La solución de un sistema de ecuaciones se obtiene al encontrar los valores de “x” e “y” que hacen que las ecuaciones sean verdaderas. Es decir, los valores de “x” e “y” que satisfacen simultáneamente las ecuaciones.
La solución de un sistema de ecuación se puede determinar a través de método gráfico o analítico.
Solución gráfica de sistemas de ecuaciones lineales con dos incógnitas.
Al graficar ecuaciones lineales de la forma ax + by = c se obtienen rectas, en este caso 2. Es decir que pueden ocurrir 3 posibles casos.
Que las rectas sean secantes, es decir se cortan en un punto. Por tanto tiene una única solución.
Que las rectas sean paralelas y no - coincidentes. Por tanto el sistema no tiene solución.
Que las rectas sean paralelas coincidentes. Por tanto el sistema tiene infinitas soluciones.
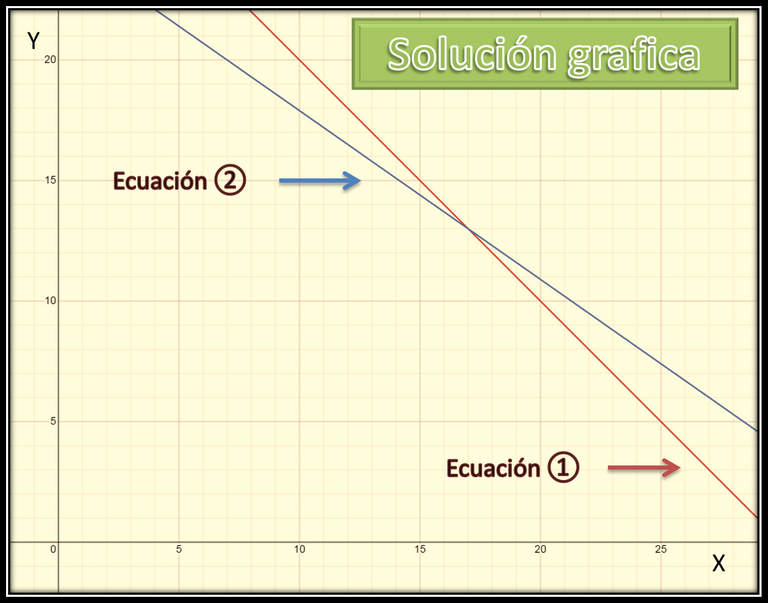
Seguidamente, realizamos el gráfico de nuestro sistema de ecuaciones.
Observamos que, las ecuaciones se cortan en el punto (13 , 17). Por consiguiente, la solución de nuestro sistema es x = 13 e y = 17. Luego, se vendieron 13 tanques de 10 kg y 17 tanques de 18 kg.
Continuemos con el ejercicio planteado en la primera sección, comprobaremos analíticamente los resultados del gráfico...
Solución analítica de sistemas de ecuaciones lineales de 2 incógnitas.
Son métodos que se utilizan para dar solución a los sistemas. En este caso, el álgebra se usa para llegar a una respuesta determinada al encontrar los valores de “x” e “y” que satisfacen las dos ecuaciones al mismo tiempo.
Los métodos más utilizados son:
Sustitución
Igualación
Reducción
Demás está decir que cualquier sea el método utilizado la respuesta arrojada será siempre la misma.
Método de sustitución
Se debe realizar un despeje de una de las variables de cualquiera de las ecuaciones y luego sustituir ese valor en la otra.
De la ecuación (1), restemos y a ambos lados. Queda:
Así:
Luego, sustituimos el valor obtenido en función de “y” dentro de la ecuación (2).
Operando, tenemos:
Reduciendo, nos queda:
Utilizando las propiedades de la adición y simplificando,
Despejando y, obtenemos:
Ahora sustituimos la ecuación (3) en (1), así:
Por propiedad de la adición y operando queda:
Por lo tanto la solución del sistema es
Solución final.
Se vendieron un total de 30 tanques de gas. 17 tanques de 10 kg y 13 tanques de 18 kg todo esto para un total recaudado de 498000 Bs.
Conclusión.
A través de esta simple problemática que puede presentar cualquier comunidad del país. Logramos hacer un estudio tangible de uno de los métodos más utilizados en las ciencias aplicadas. El cual consiste en modelar matemáticamente situaciones que podemos encontrar en nuestro día a día.
Por otro lado, que este simple enfoque no menosprecie el alcance del método, ya que es usado en innumerables ámbitos de nuestra sociedad. La economía, la biología, la industria, la física, la astronomía, entre otras. La intención es lograr un compendio de números con el objetivo de crear una noción clara sobre lo transcendental que ha significado este enfoque para la evolución de nuestra humanidad.
Referencias bibliográficas

Creator: @yonnathang
Ilustration: @yonnathang
Recommendations:
El TEAM -MEXICO 
Intrepreneur 
Proyecto votoVzla
MayVileros
RadioSteemit
SteemBasicIncome


El álgebra es una cátedra fundamental para cualquier carrera de ciencias puras e ingeniería. En este caso el sistema de ecuaciones lineales es fundamental para la resolución no solo de problemas matemáticos abstractos, si no también muestra que tiene su aplicación en diferentes ámbitos de la vida como lo acabas de plasmar en tu contenido. Saludos!
Saludo!
Cierto, esta temática es primordial al momento de ir a las ciencias aplicadas. Por tanto, se hace necesario que sea dominada a plenitud por esos futuros ingenieros.
Gracias!
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider using the steemstem.io app and/or including @steemstem in the list of beneficiaries of this post. This could yield a stronger support from SteemSTEM.
Thank you!
Saludos @yonnathang!
Es un gusto visitar tu blog,
en esta ocasión veo que traes un post con información
técnica valiosa.
El contenido está muy bien redactado y la evaluación que
has hecho acerca de la problemática de distribución del gas
doméstico en nuestro país ha sido bien explicada.
La aplicación de las matemáticas así como el empleo de gráficos
explicativos logra que la información sea práctica y más fácil de
asimilar...
Que bien que hayas tomado en cuenta este punto tan importante
relacionado con los servicios y suministros indispensables
para el desarrollo de nuestras vidas.
Apoyo total, hermano, espero que tu publicación trascienda
dentro de la plataforma y sirva como referente para los demás
usuarios!
Hasta la próxima,
Te veo pronto
@nachomolina
#venezuela
Gracias por el apoyo amigo.
Trataremos de seguir compartiendo este tipo de información. Como lo vaya permitiendo el tiempo. Mientras, seguimos trabajando!
Saludo fraterno...
Curamos la etiqueta #spanish con el token SPACO de la Comunidad de Hispano Hablantes, te invitamos a formar parte de nuestra comunidad.
Gracias por su apreciación!
Wao, me has dado una idea, gracias por el aporte :3 Aquí apoyando el buen contenido jeje
Gracias! Me avisas cuando compartas tu idea.
Congratulations @yonnathang! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOP