Enseñanza de la física usando imágenes en movimiento - Vectores
Enseñanza de la física usando imágenes en movimiento y la plataforma HIVE BLOG - Vectores y aplicaciones
En una clase magistral un profesor puede requerir del apoyo de recursos educativos diferentes a los tradicionalmente usados como el pizarrón, la tiza o el marcador. En la enseñanza de la física, por ejemplo, es muy útil usar herramientas tales como modelos didácticos, experimentos recreativos de escritorio [1], videos y proyecciones de diapositivas. Sin embargo, hoy en día la educación a través de la escuela virtual con el uso del internet es cada vez más utilizada y representa un reto para los profesores, particularmente para los que imparten clases de ciencias básicas: matemática, física y química.
En la red del internet existe una gran variedad de lugares que los estudiantes pueden visitar fácilmente, ya sean páginas web de universidades o de particulares.
Como profesor universitario he querido aprovechar esta maravillosa plataforma de HIVE BLOG para crear y desarrollar una serie de clases originales. La idea principal es el uso de animaciones sencillas que ayudarán enormemente al entendimiento de las ciencias físicas que abarcan temas que van desde vectores hasta la dinámica de una partícula e incluso más allá.
Las clases virtuales tienen grandes ventajas, pero también posee puntos débiles, por ejemplo, cuando las clases no son impartidas en tiempo real el alumno observa un video del profesor explicando un tema determinado, sin embargo, si al estudiante le surge una duda él no podrá interactuar de inmediato con este último, de hecho es posible que esa inquietud del estudiante sea olvidada o desestimada a posteriori.
En una clase magistral no solo pueden surgir dudas o inquietudes de parte del estudiante sino también del mismo profesor, sea de quien sea la duda cuando esto sucede surge inmediatamente la oportunidad por parte del docente de discernir o indagar junto con los estudiantes una mejor forma de explicar o enseñar un tema o problema determinado y esto casi nunca sucede en una clase virtual.
En este sentido pienso que el uso de animaciones puede sustituir el aspecto de los detalles visuales que muestra un profesor en sus clases, tales como gráficas auxiliares, ejemplos o comparaciones que surgen en clase cuando el estudiante pregunta al profesor o este último aprecia que hay ciertos vacíos en su explicación. Mi intención es que el estudiante pueda apreciar las partes principales de un problema y como están relacionadas directamente en su solución, y de esta manera evitar la distracción por parte del alumno en elementos que no son relevantes en la resolución del mismo.
En esta oportunidad, y en próximas entregas, explicaré paso a paso la solución de problemas que según mi experiencia como docente crean cierta dificultad y confusión cuando el estudiante trata de resolverlos, y que son frecuentemente consultados para ayudar a su solución. Pienso que esto sucede porque el problema muchas veces carece de ciertos detalles visuales que ayuden al estudiante a ver y entender lo que está sucediendo en el planteamiento, y es aquí donde las imágenes animadas ayudan enormemente al entendimiento y solución de estos problemas físicos.
Prolema 1.
La bandera situada en el mástil de un bote a motor flamea haciendo un ángulo de 45° suroeste, otra bandera situada en una casa a la orilla del lago se extiende por el viento 30° suroeste. Usando el método del triángulo y del paralelogramo calcular: a) la magnitud de la velocidad del viento si la magnitud de la velocidad del bote es de 10 km/h, b) encontrar la magnitud de la velocidad aparente del viento para un observador situado en el bote, c) expresar los vectores de velocidad involucrados en el problema con sus respectivas componentes.

Solución
Graficamos los vectores correspondientes a las velocidades involucradas y conocidas en el problema y los trasladamos todos al origen de un sistema de referencia común. (Ver Figura 1)
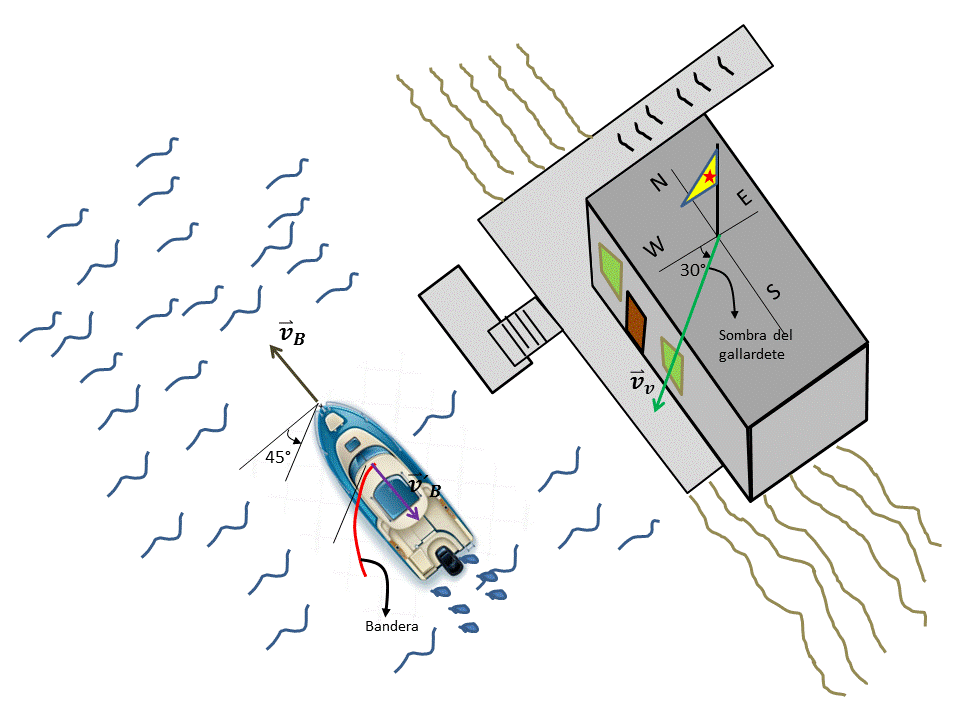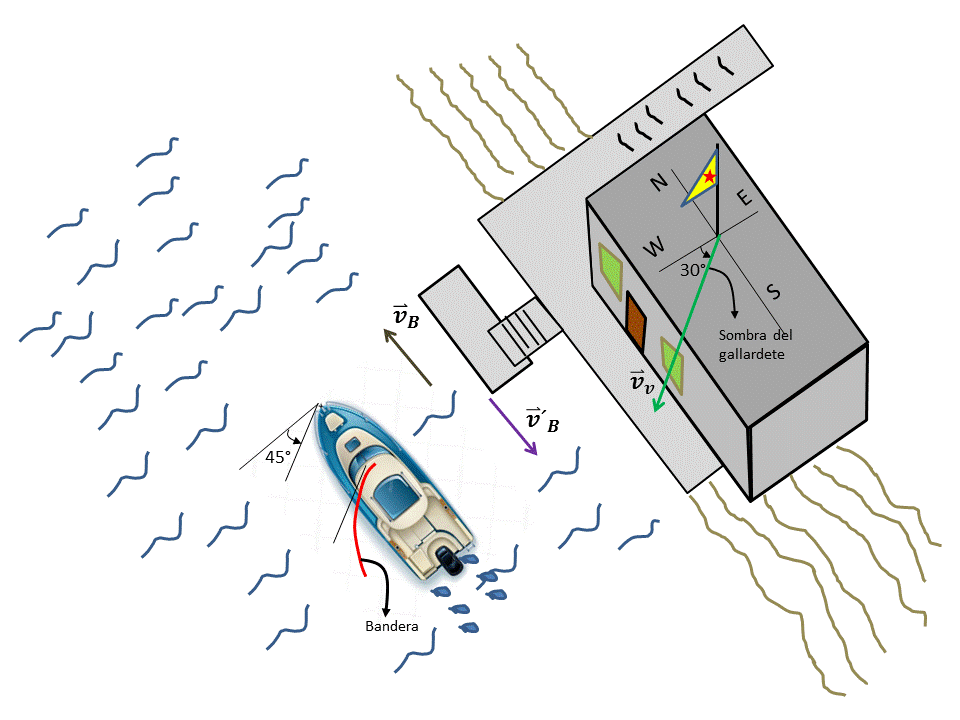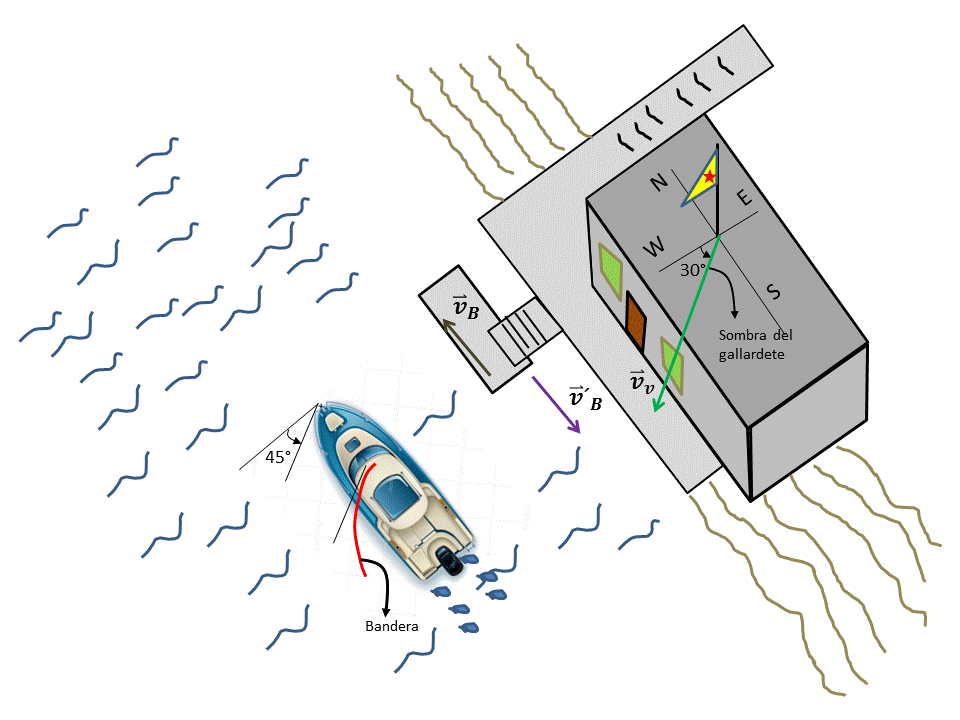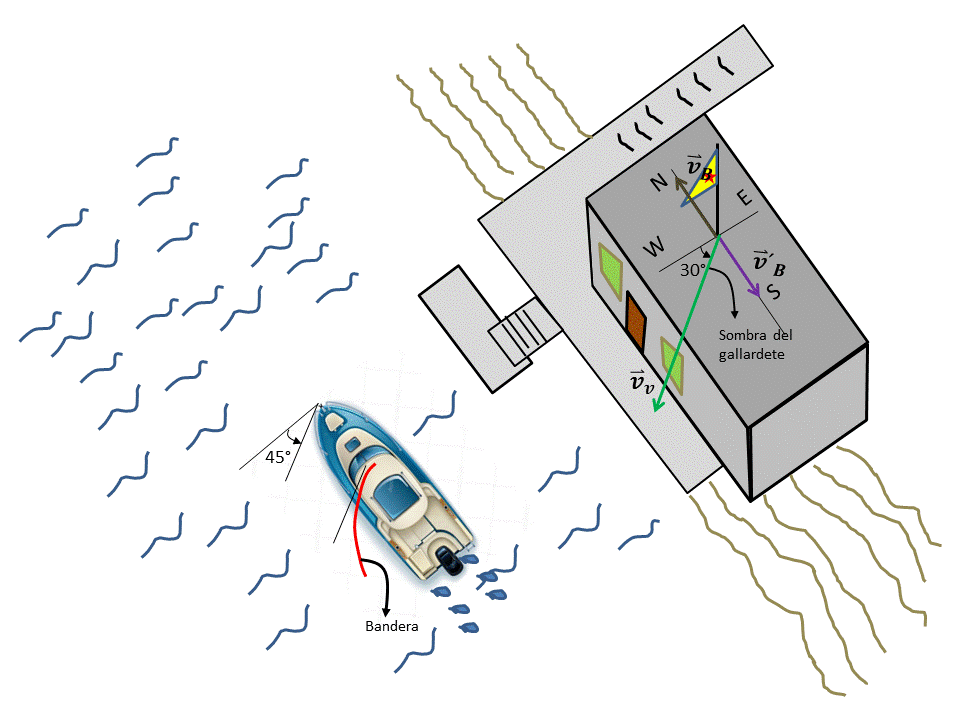
Figura 1. Traslado de lo vectores correspondientes a las diferentes velocidades al origen de un sistema de coordenadas común.
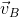 : velocidad del bote en la dirección norte.
: velocidad del bote en la dirección norte.
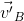 : velocidad de arrastre provocada por la velocidad del bote y el aire, ésta es opuesta a la velocidad del bote pero tiene su misma magnitud.
: velocidad de arrastre provocada por la velocidad del bote y el aire, ésta es opuesta a la velocidad del bote pero tiene su misma magnitud.
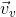 : velocidad desconocida del viento en la dirección W30°S.
: velocidad desconocida del viento en la dirección W30°S.
Las velocidades 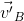 y
y  provocan que la bandera que está en el bote flamee en dirección W45°S, es decir hay una velocidad aparente que está dada por la siguiente relación:
provocan que la bandera que está en el bote flamee en dirección W45°S, es decir hay una velocidad aparente que está dada por la siguiente relación:
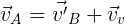
Gráficamente esta suma de vectores con sus respectivos ángulos con los ejes coordenados (direcciones) puede observarse en la figura 2. Como podemos apreciar se ha usado el método del triangulo.
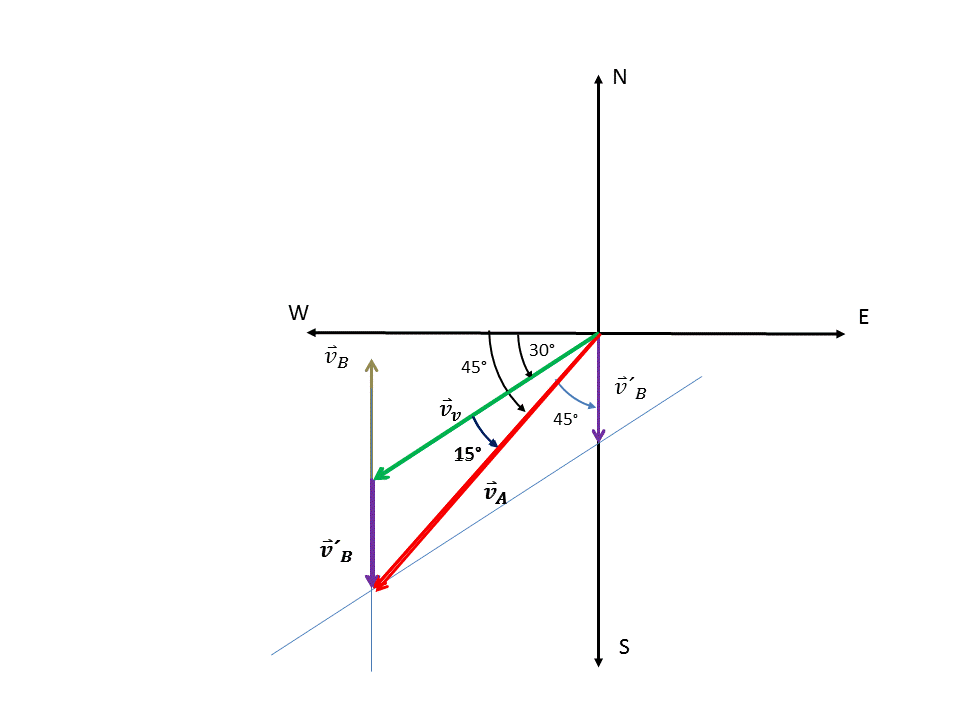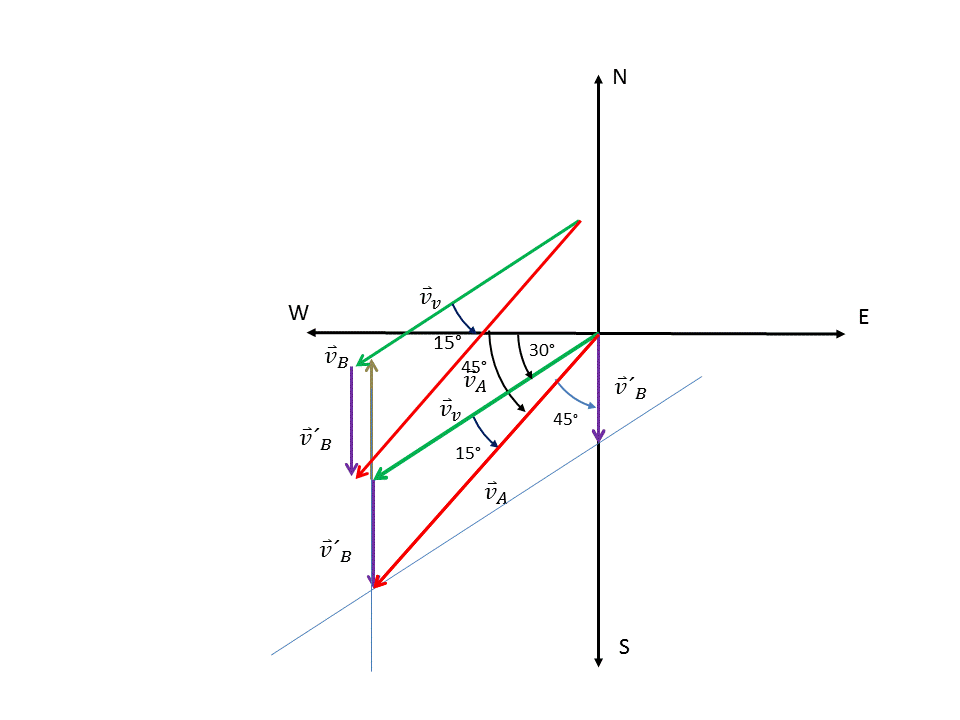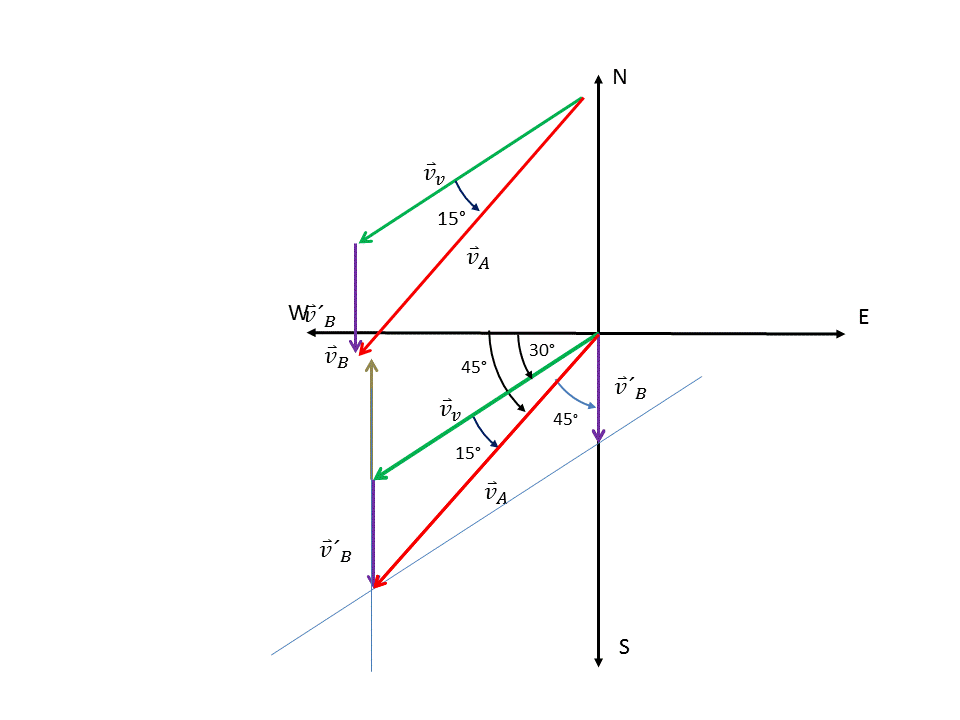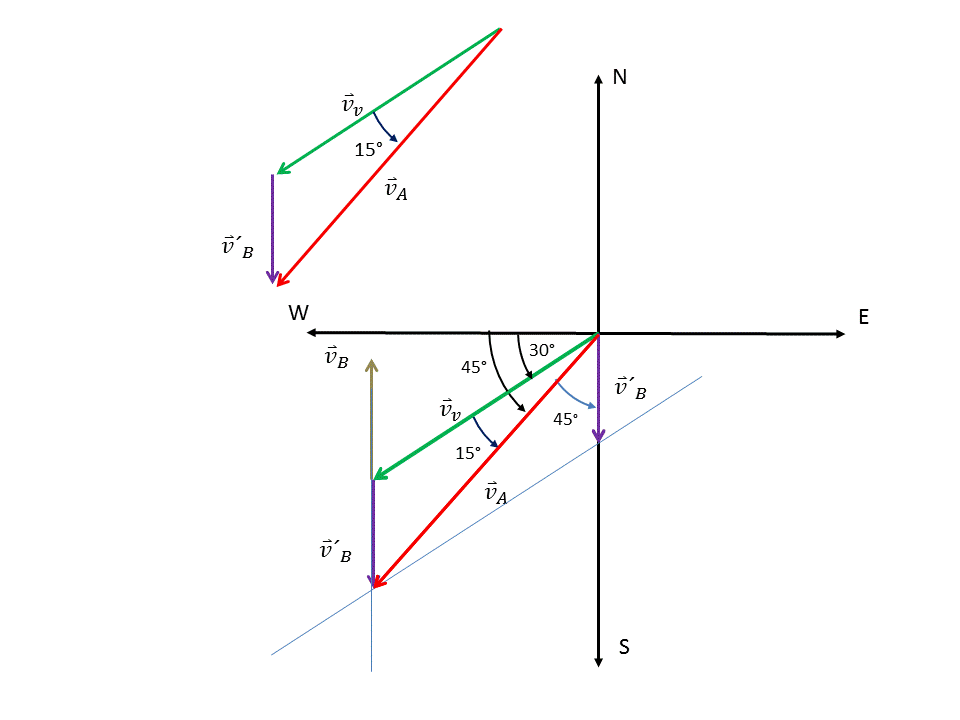
Figura 2. Suma de los vectores 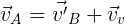 usando el método del triángulo
usando el método del triángulo
Entonces obtenemos el siguente triángulo
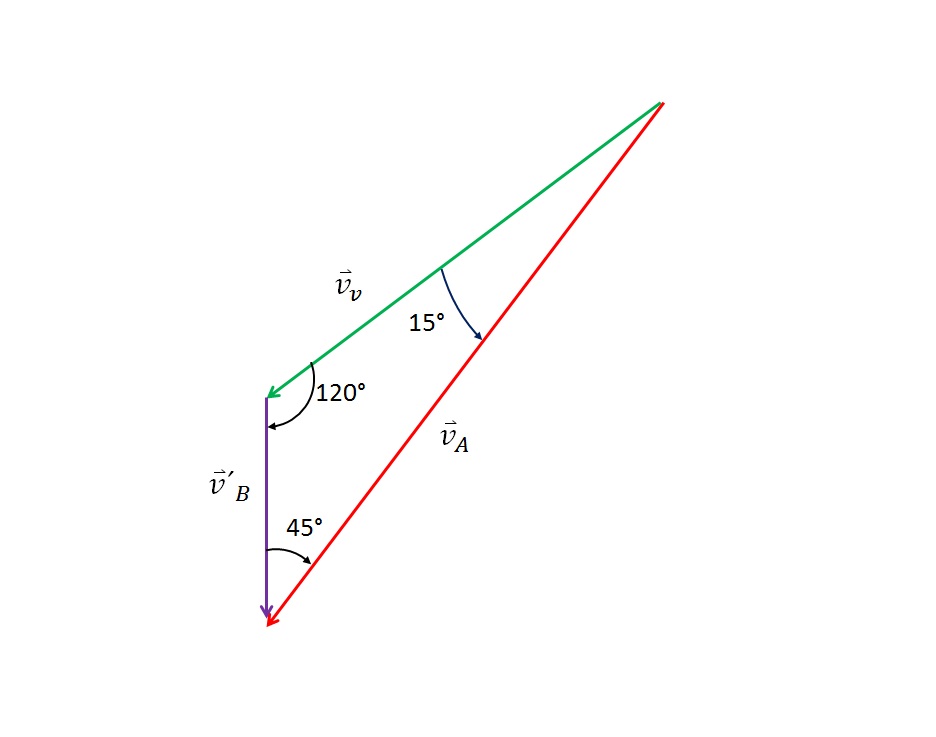
Si observamos la animación podemos ver que el ángulo en el vértice formado por 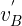 y
y 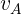 tiene que ser de 45° y el ángulo restante es de 120° ya que la suma de los ángulos internos de un triángulo debe ser igual a 180°.
tiene que ser de 45° y el ángulo restante es de 120° ya que la suma de los ángulos internos de un triángulo debe ser igual a 180°.
Aplicamos la ley del seno
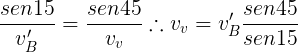
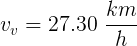
Aplicando de nuevo la ley del seno podemos hallar la velocidad aparente.
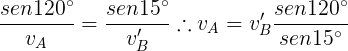
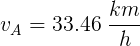
Podemos usar también el método del paralelogramo para hallar 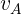 (Ver figura 3)
(Ver figura 3)
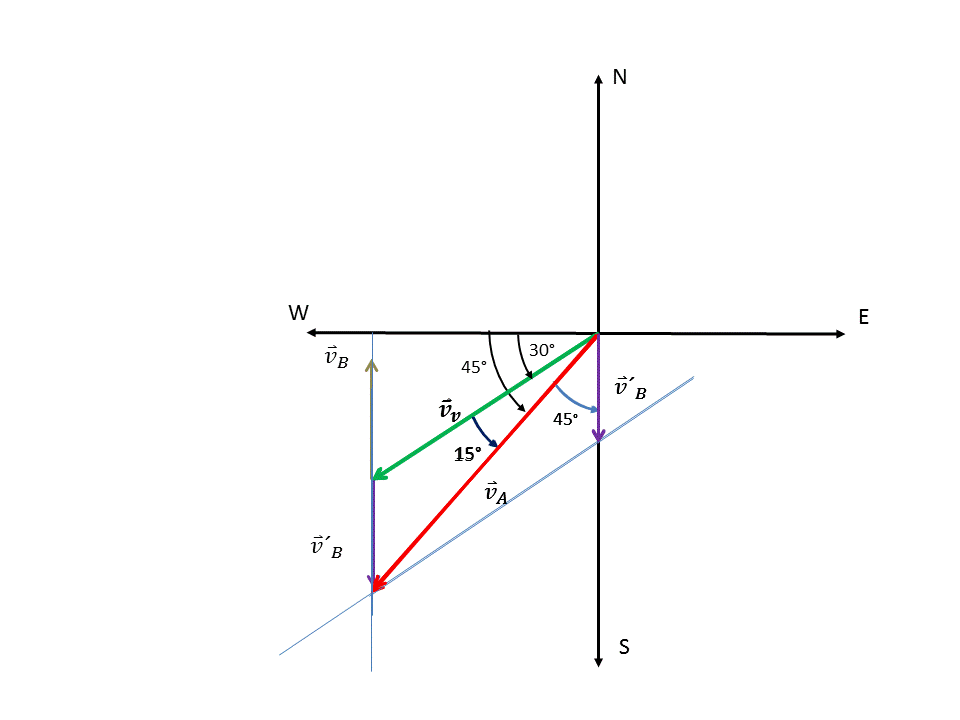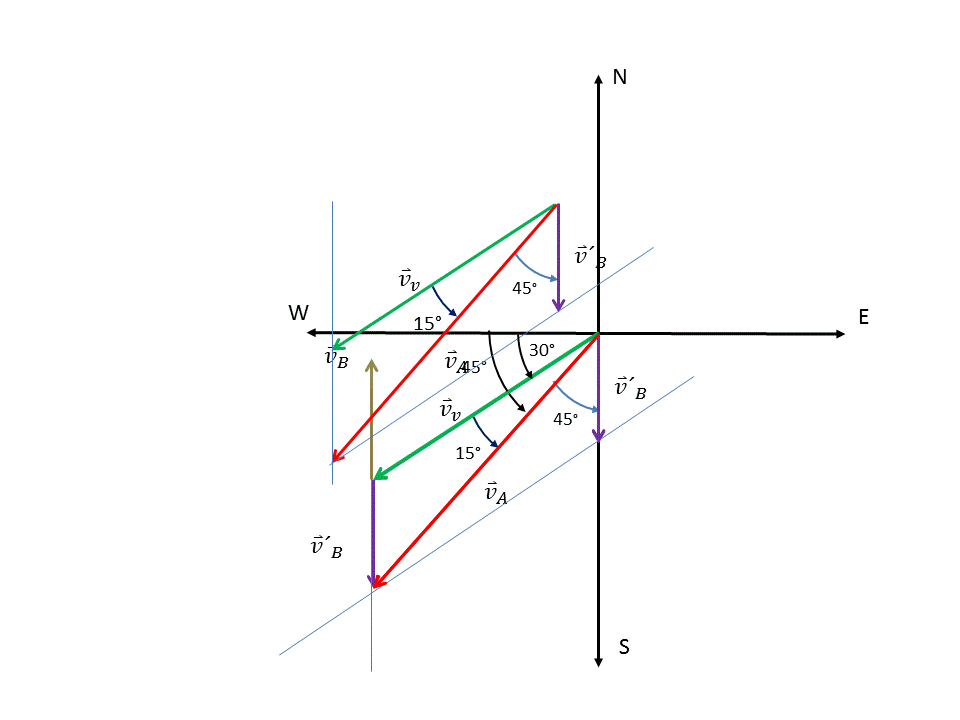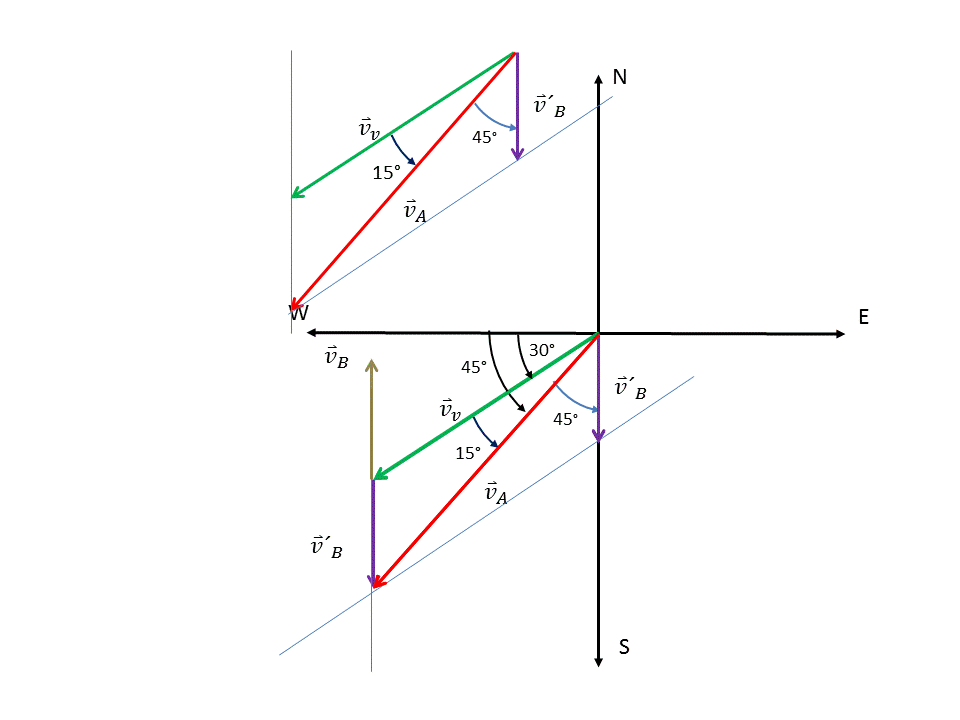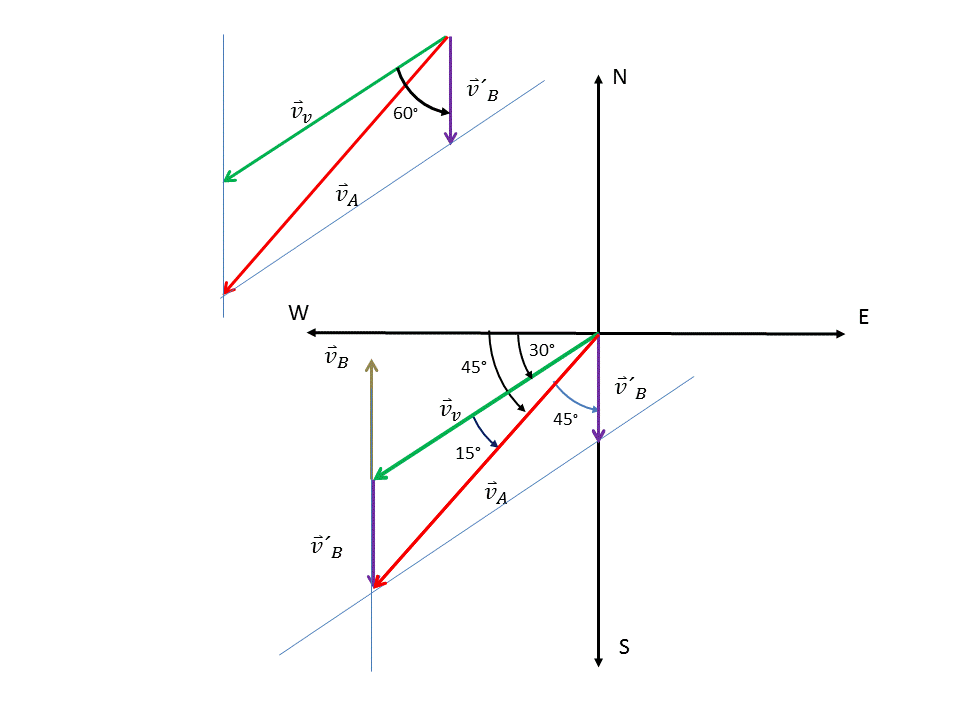
Figura 3. Suma de los vectores 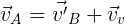 usando el método del paralelogramo
usando el método del paralelogramo
Entonces obtenemos el siguente paralelogramo
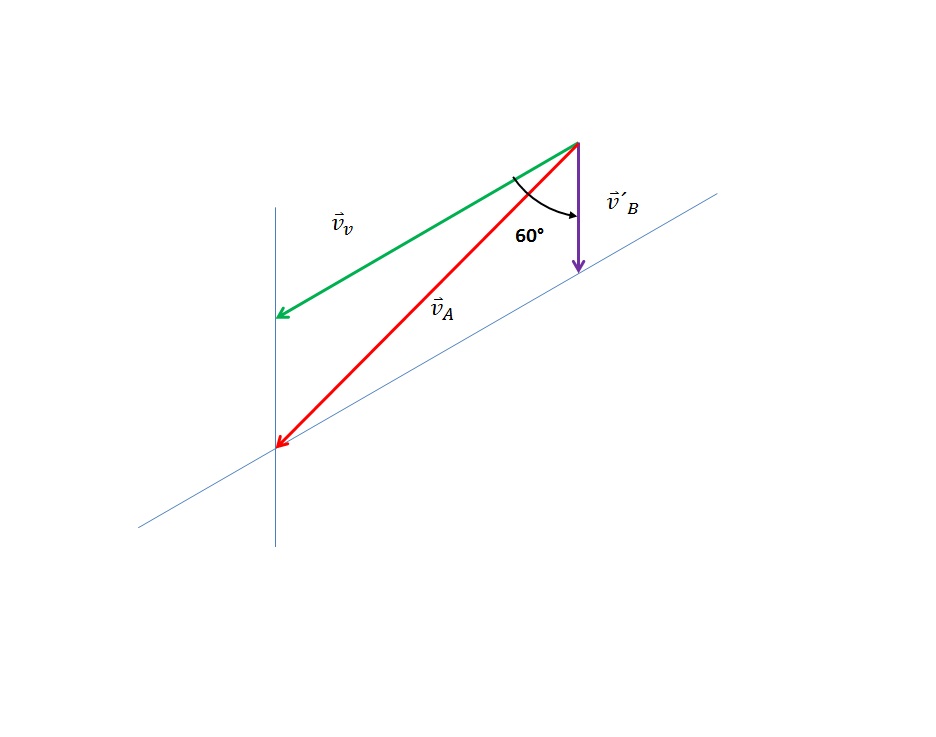
Para hallar 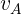 usamos la siguiente ecuación [2] :
usamos la siguiente ecuación [2] :
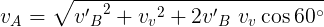
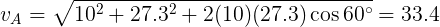
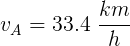
De esta manera hemos obtenido las magnitudes de las velocidades involucradas en el problema, es decir, la rapidez. Pero ahora procedamos a hallar por separado los vectores con sus respectivas componentes.
La velocidad del bote es hacia el norte franco, por lo tanto sólo tiene una sola componente en dirección del eje "+y", de igual manera como la velocidad de arrastre tiene la misma magnitud pero dirección opuesta a la velocidad del bote entonces esta tendrá dirección hacia el eje "-y". Ver figura 4. Por lo tanto las velocidades del bote y de arrastre vendrán dada por los siguientes vectores respectivamente:
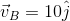
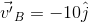
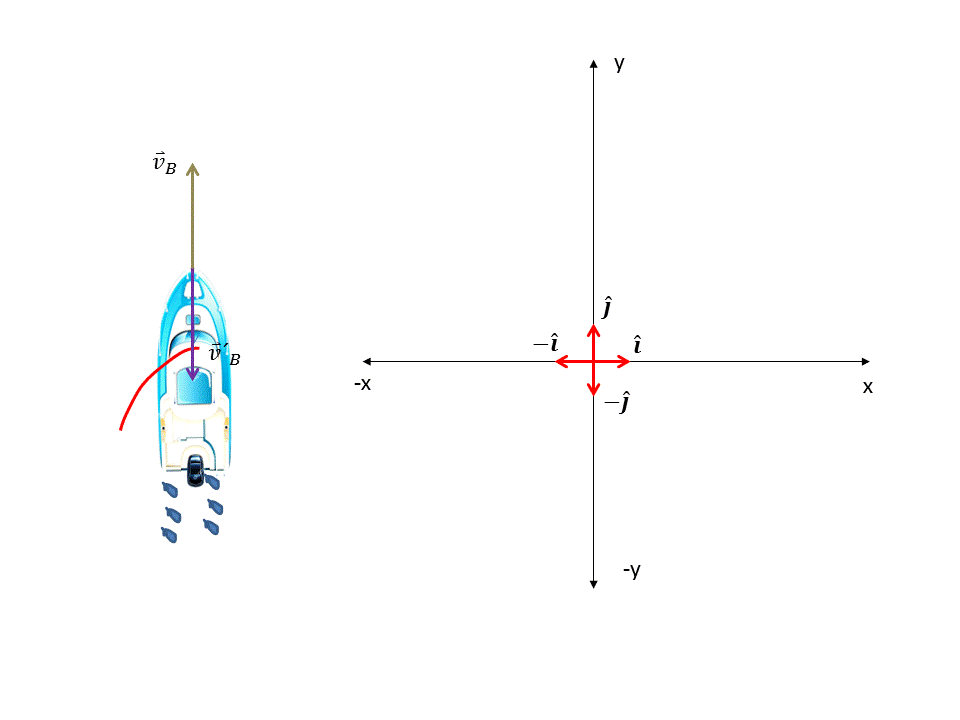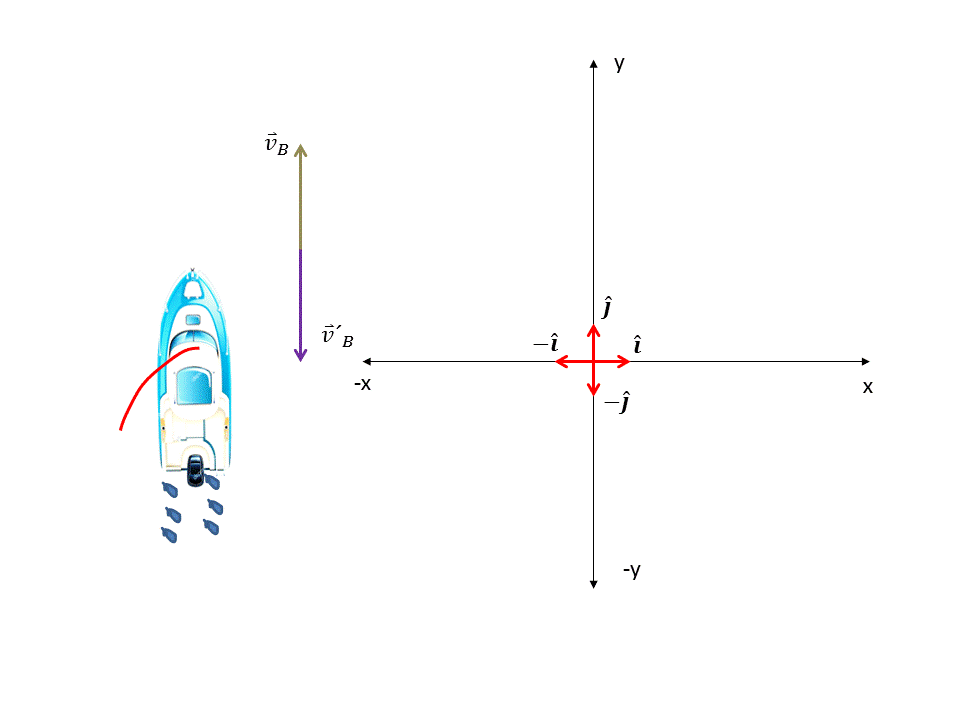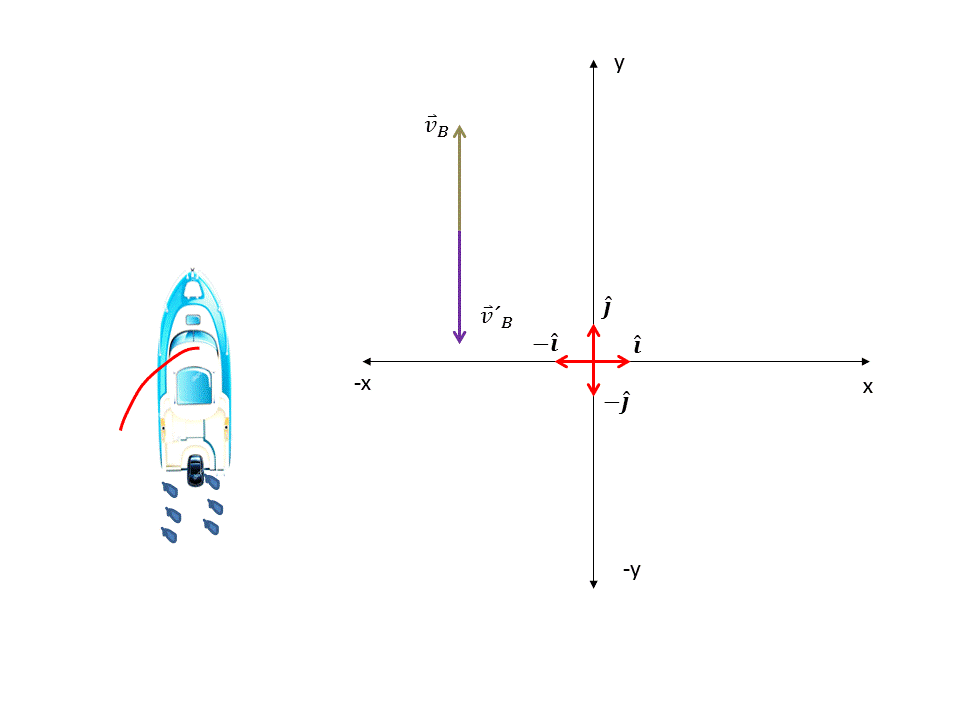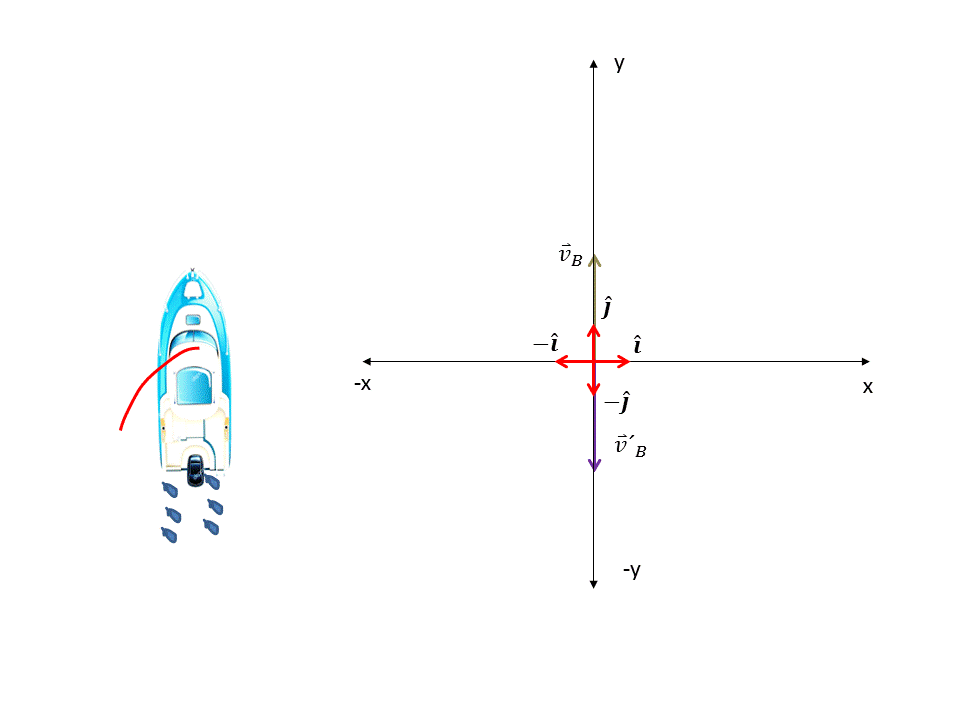
Figura 4. Velocidad del bote y velocidad de arrastre
Procedemos ahora a obtener la velocidad del viento. Como hace un ángulo de 45° con el eje "-x" calculamos por simple trigonometría las componentes en cada eje. Ver figura 5.
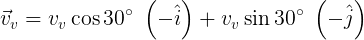
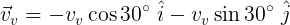
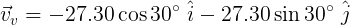

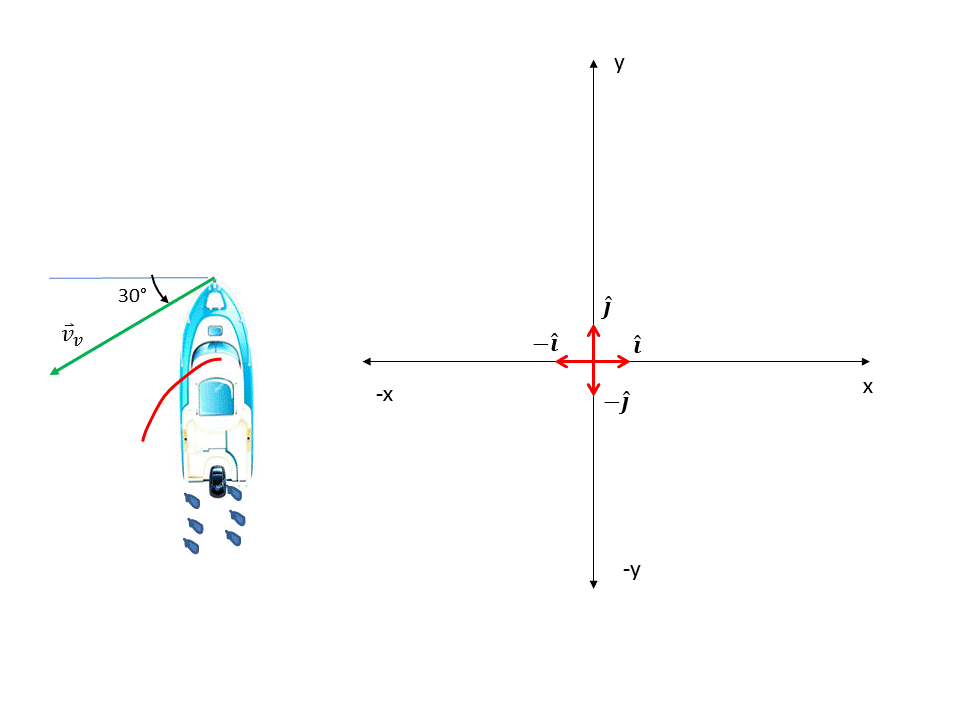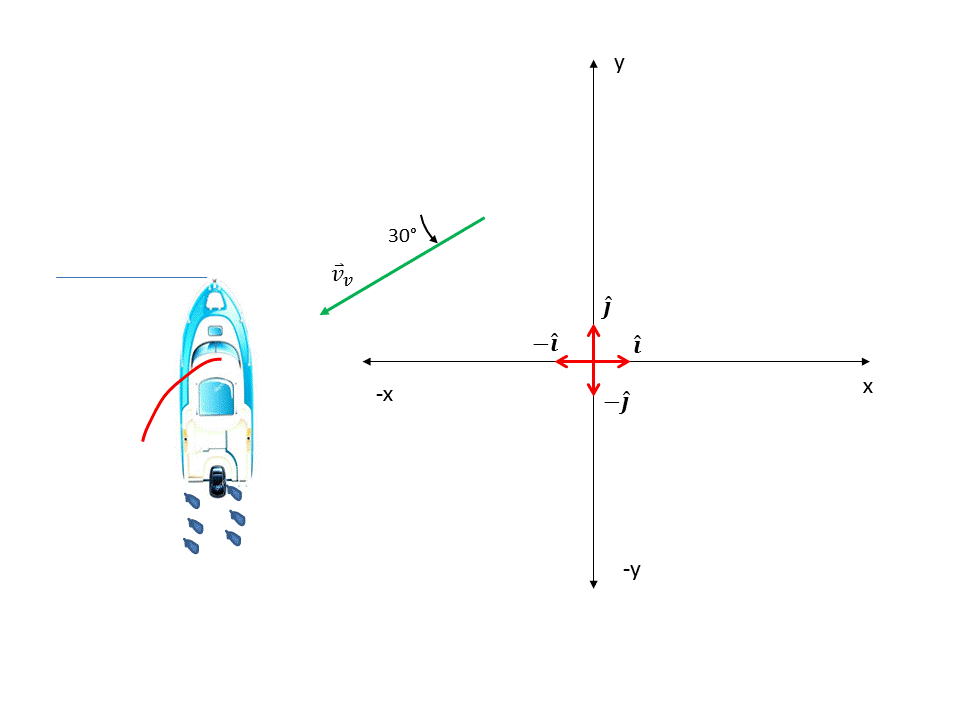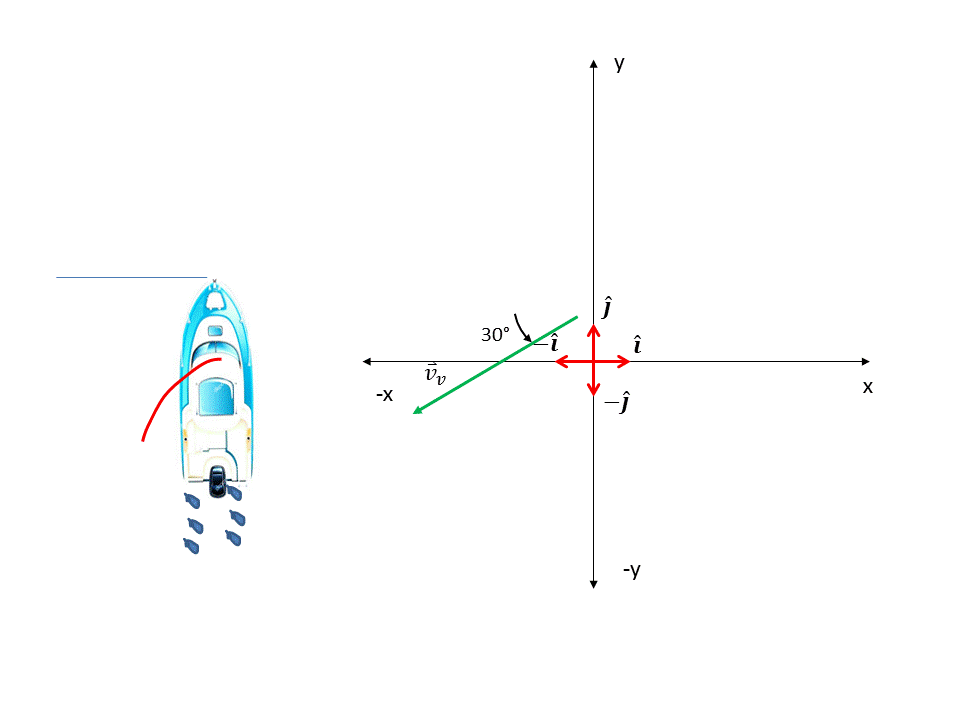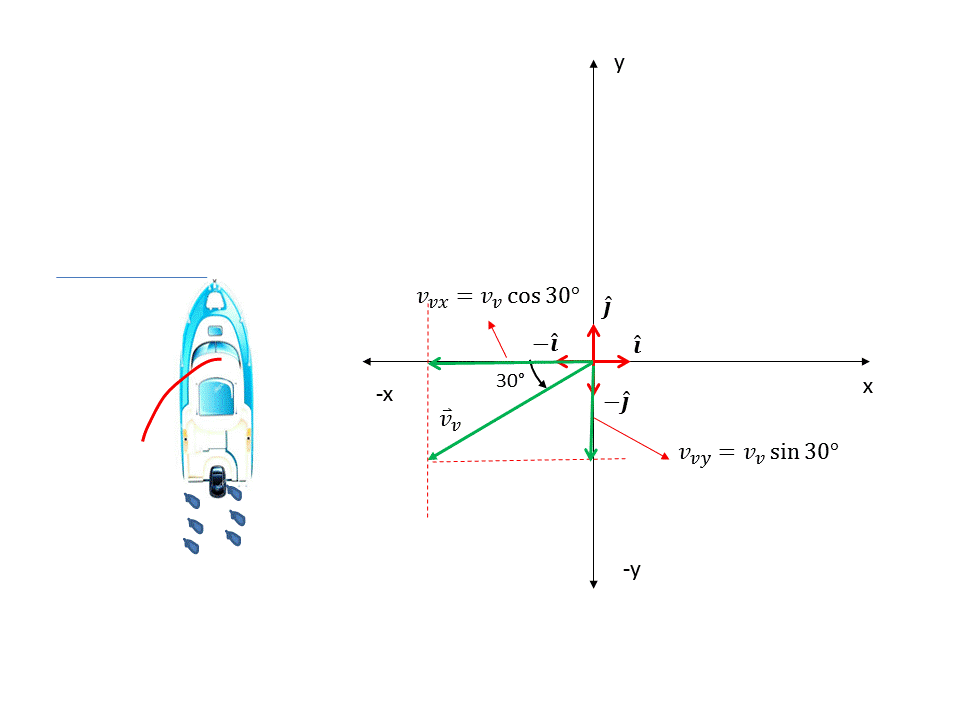
Figura 5. Componentes de la velocidad del viento
Ahora calculamos las componentes de la velocidad aparente, esta hace un ángulo de 45° con el eje "-y". Ver figura 6.
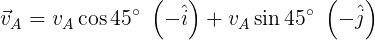
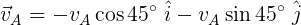
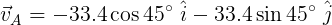
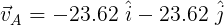
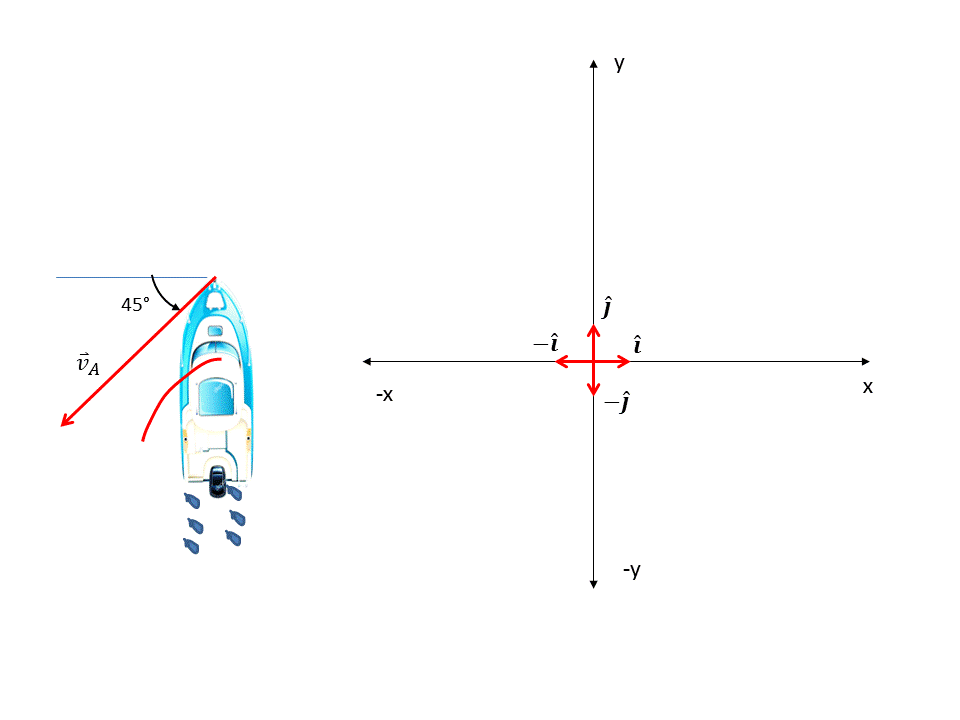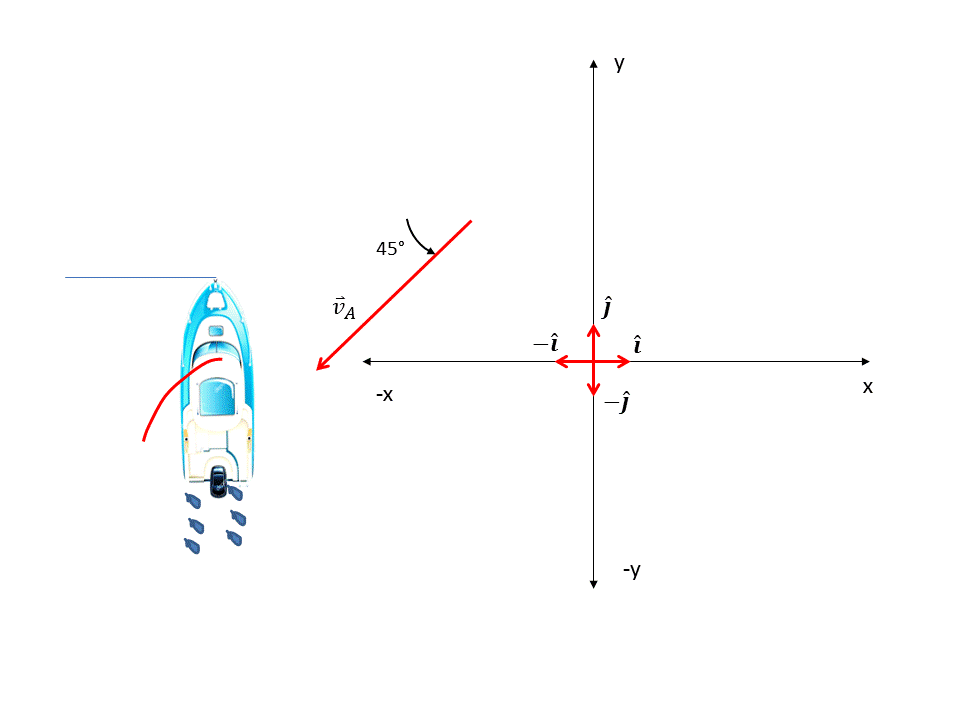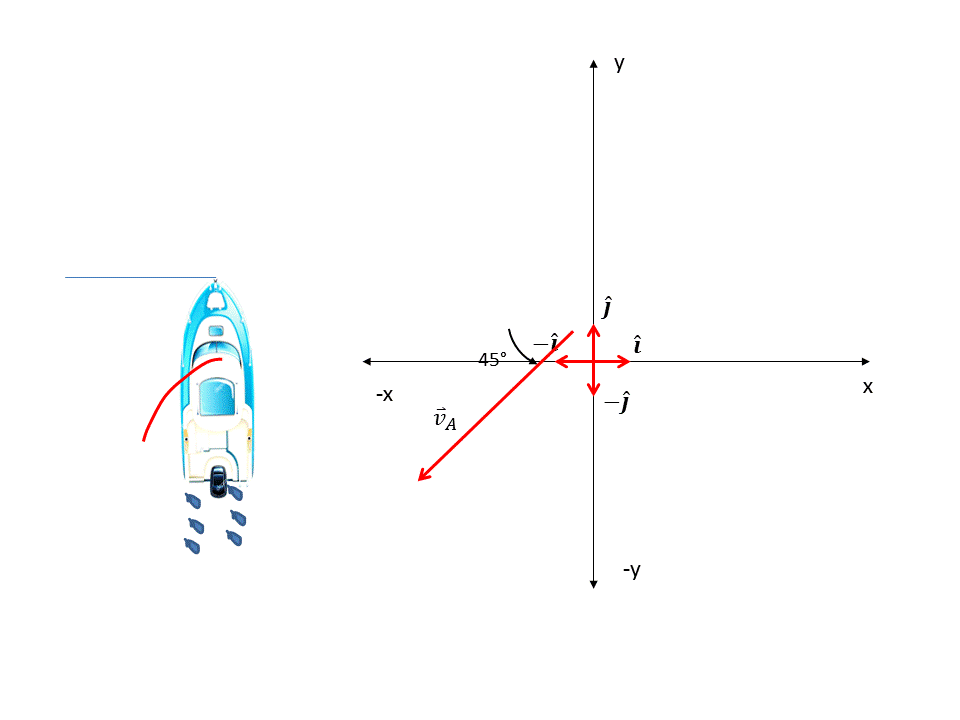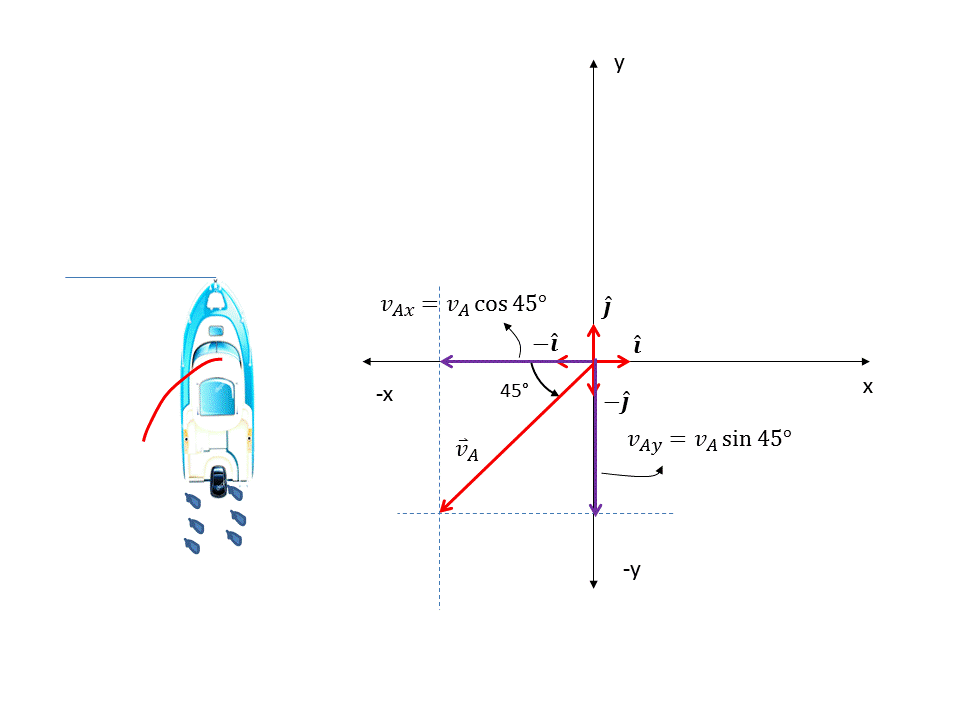
Figura 6. Componentes de la velocidad aparente
Como hemos podido apreciar las imágenes o figuras animadas ayudan mucho a la solución y comprensión de un problema, la geometría y trigonometría juegan un papel importante y una buena descripción gráfica permite identificar rápidamente las variable involucradas (velocidades en este caso) en el problema.
Para concluir pienso que el uso de animaciones es una gran ayuda para el profesor cuando se requiere explicar una clase no presencial por medio de herramientas tecnológicas. El uso de la plataforma HIVE BLOG permite y facilita la divulgación de las clases debido a su popularidad y fácil acceso en las redes sociales.
This post has been voted on by the STEMsocial curation team and voting trail. It is eligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @steemstem account (for some ROI).
For additional information please join us on the STEMsocial discord and to get to know the rest of the community!
Please consider using the stem.openhive.network app and including @steemstem as a beneficiary of this post. This could yield a stronger support.