Schrödinger, the inventor of the master equation of quantum mechanics

After a short break due to a busy period in my offline life, here I am, back with a new post on quantum mechanics.
In the previous episodes, I have described how a wave (or actually light) could also possess the behavior of a particle (see here). In a second article, I swapped those concepts and I discussed the fact that a wave could also be attached to any particle (see here).
This is the concept of wave-particle duality. With each wave comes a particle and vice-versa: which each particle comes a wave. I have given more details about that in my last quantum mechanics post, here.
It is now time to move one step further and get our hands dirty: a wave obeys to a wave equation. But what is the equation governing the behavior of the matter waves?
What? Equations? Aouch…
However, please do not be afraid. I am in a partial half-good mood and I will try to make this post only half-dirty. Some equations will be there, as they cannot be avoided entirely (at least I do not know how to do so).
I will however try to have way more text than equations so that the reading of the post will be kind of easy going. Please let me know whether I succeeded. And do not hesitate to complain and ask for clarifications if needed. ^^
THE CONSTRUCTION OF THE SCHRODINGER EQUATION
Once physicists were convinced that matter waves were existing, the next natural step was to find an equation which those matter waves were solutions of.
It is Erwin Schrödinger (the guy of the picture below) who has built this equation, about 25 years after that the notion of a quantum of energy was introduced.

[image credits: Wikipedia]
The way in which Schrödinger designed his equation was not a proof, but a heuristic approach.
He started from the information he had in the beginning of the 20th century and from these pieces of information, he imagined an equation that could work and describe the behavior of the matter waves.
By virtue of its success, this equation now carries Schrödinger’s name.
The amazing thing is that Schrödinger managed to construct an equation way more general than the basic elements which he started from.
The two ingredients used by Schrödinger were the following. First, he knew that the relations proposed by de Broglie have to be reproduced. This means that (beware, first equation ahead!)
p = ℏ k and that E = ℏ ω
In this equation, the vector p denotes the momentum of the particle and E its energy. I recall that the momentum is a quantity that mixes mass and motion and is defined as the product of the particle mass by its velocity. Moreover, the constant ℏ is the reduced Planck constant (ℏ= h/2π), k is the wave vector (or in other words the direction in which the wave propagates), and ω the wave pulsation (or its frequency, more or less).
The second ingredient used by Schrödinger was the fact that he knew that classical mechanics is working at the macroscopic level. Therefore, all the relations induced by classical mechanics are valid and must be recovered in some limit.
MERGING CLASSICAL MECHANICS WITH MATTER WAVES
The reasoning of Schrödinger started by considering a particle of mass m moving freely, not interacting with anything. Its energy is thus simply its kinetic energy, and here is the second equation of this post,
E = p2 / (2 m)
Classical mechanics at work! Nothing less, nothing more. The energy equals the norm of the momentum squared, over twice the particle mass.

[image credits: Wikipedia]
But the squared momentum and the energy are also the two quantities given by the relations of de Broglie shown above.
Putting everything together, one derives the fact that the pulsation of the matter wave is proportional to the wave-vector squared,
ω = ℏ k2 / (2 m)
And this is an amazing relation.
Waves are usually introduced as light waves. In this case, the pulsation is proportional to the speed of light and the norm of the wave vector. Here, we have a totally different relation. The pulsation ω is proportional to the norm of the wave-vector squared k2…
TOWARDS THE FORM OF SCHRODINGER EQUATION
So what have we learned so far? Let us summarize.
We have a wave that propagates in a direction (cf. its wave-vector k) that is aligned with the particle momentum p (cf. the relations of de Broglie ), or in other words with its velocity (as the momentum is proportional to the velocity).
All this to say that the wave propagates parallel to the motion of the particle.

[image credits: Wikipedia]
A wave is a function that depends on the position and on the time, and the simplest possible wave is a plane wave.
I could give the equation… But actually, I will not (enough equations here… for now).
What is important to know is that a plane wave has two important properties.
When a plane wave is derived once with respect to the time, one gets the pulsation of the wave. When a plane wave is derived twice with respect to the position, one gets the norm of the wave-vector squared.
But we have just explained in the previous section that in the case of matter waves, the pulsation is proportional to the norm of the wave-vector squared.
Yes! We have our wave equation: the first derivative of the wave with respect to time is roughy equal to the second derivative of the wave with respect to the position,

GENERALISATION - THE CORRESPONDENCE RULES
The equation above (I know, we start to have a lot of equations around here) can be derived immediately from the classical definition of the energy by using so-called correspondence rules. These rules consist of replacing physical quantities with operators (or derivatives).
We start from the classical definition of the energy already given at the beginning of this post,
E = p2 / (2 m)
We then add a wave 𝜑 on both sides, replace the energy by a time derivative and the momentum by a space derivative, and we get the last relation.
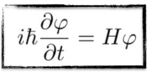
[image credits: homemade]
These correspondence rules allow for an easy generalization to the case where we have interactions, as shown on the left.
The quantity on the right-hand side of the equation H is now the Hamiltonian. It is a mathematical object that contains the kinetic energy and the potential energy (relevant when interactions are in order) and whose exact form is derived using the correspondence rules.
Of course, the reality is slightly more complex to what I have sketched here. But not that much actually :)
A SHORT DISCUSSION AND REFERENCES
With this post, I wanted to explain how the main equation of quantum mechanics was born. It has been originally found by Schrödinger by using classical physics (as a working limit of quantum mechanics) and de Broglie findings for matter waves.
It is a bit hard to me to introduce Schrödinger equation without relying too much on equations. I tried to do my best to make this post simple enough. Please, let me know whether I have succeeded :)
For more information (and references), one can check either this book, or the various links provided in the post.
Table of contents of this series of posts
I. Introduction
1. Concepts and fundations
2. Interactions and conservation laws
3. Systems of particles
II. The origins of quantum mechanics
1. Fundamental physics at the beginning of the 20th century
2. The mysteries of the atomic spectra
3. The mysteries of the black bodies
4. Quantization of the electromagnetic radiation and the birth of the photons
5. The Compton effect
6. The planetary model of the atom
7. The Bohr model of the atom
8. Matter waves
9. More on the wave-particle duality
10. The Schrödinger equation (this post).
For more discussion on this topic (or anything related to science), please join us on steemSTEM. SteemSTEM is a community driven project which seeks to promote well written/informative Science Technology Engineering and Mathematics postings on Steemit. More information can be found on the @steemstem blog.
We are currently consolidating the steemSTEM curation trail by different means. In the case where you would be interested, please contact us on the chat.
Sir can I resteem your post?
Yes, you can
Resteem done! please my cheek blog. Maybe you can collect some important information from my post. Let me say a word if you do not mind, if you please give me an upvote, then I will be grateful to you forever.
https://steemit.com/life/@sagor5828/more-than-four-cups-of-coffee-is-sure-to-die
If I can give you an advice, advertising his own posts on the blog of someone else and begging for upvotes is not the best way to get some. Just engage people nicely, and they will give you upvotes. Believe me, it works :)
That sounds very obama-ish ;)
@lemouth, come to think of it I never intended for it to come out like that. But that's Obama right there on his campaign trail with his yes, we can :)
:)
Well, why not? :)
Nice share.
https://steemit.com/dtube/@fremy/lkrbdoeu
Thanks a lot
As I said above, this sort of advertisement is not the best way to get views and comments. I would prefer 1000 times someone engaging the discussion than just link dropping. And I am ont the only one :)
thank you for telling me about it. on another occasion I will try to discuss with you.
The equations ain't that scary. You made it easy to read. I bet others would say the same, even the non-science students. This made me remember a lecturer we nicknamed Eigenvalue because of his love for it :) Thanks for sharing.
Thanks! I am always feeling uncomfortable when writing equation. There is a proberb saying that with each equation, one looses 1/3 of the readers :D
That's very correct, unless of course you are posting at nerd.com :D
Does that exist for real? :D
I just typed it in now and found out there is such a website. I totally have no idea there is such a website. Wow. Mind totally blown :)
Same here. Am laughing out loud :)
We love the internet. Lol
Reading your comment and I also tried the website!
For a nerd stuff, the site is awefully simple XD
@pisolutionsmru, they do not want to scare anybody away :)
It was so simple that it scared me away :p
@pisolutionsmru, lol
Unfortunately nerd.com doesn't have posts, not even from nerds.
@point, just a chance comment...never even know a website like that exists :)
Yeah I didn't know about either, until you mentioned it as a joke. But it's an excellent name for a website to post nerdy type posts if only they did that.
I am Sarah from Algeria and interested in traditional Algerian clothes. I hope you will take care of my special page. Thank you
I am not too sure this is related to my post...
Schrodinger's equation was only mentioned once in my year one at the University when we studied wave-particle duality. You seem really worried about those formulas but those that would understand what you're talking about in the first place would not mind the few formulas at all. Well explained.
But wait, is it just me or does Schrodinger look like Richard Quest?
As I said below, the problem with the formulas is that they consist in the best way to loose readers. And the lost readers are usually those not commenting... So yes I am slightly worried :)
PS: I just google Richard Quest... I agree, they look quite alike ^^
Hahahaha. You're right. I didn't think about those not commenting. Quest Means Business 😊
what did you study ? i have used it a lot in chemistry!
Quantum physics is indeed not only used in physics today :)
I studied Electrical Engineering. Thanks for your reply.
Cool
Erwin Schrödinger was a very good man, though he was not the only one, and he got ideas from others like bohr . with the wave fiction for election quantum levels, it is indeed a feat.
He was once my favorite scientist, really enjoyed his method of thinking.
A field is often moving from a synergy between many individuals. One can have a great idea, but it is always based on knowledge developed by others. This is one of the greatness of science. Collaborations without any border of any kind :)
Valid point. It always boils down to what is achieve-able and how many possibly can it cover. From perspective, he is outstanding.
You are WAY better than Sheldon Cooper.
The only think I can say is that at least, I am real :p
Thanks for the message :)
First, I am not a physicist. Secondly, you are pulling me very gently in a physics discussion, and you have succeeded in doing that. You must be a great teacher. . Physics is too complicated for me but you make it so interesting that I can not jump even a single letter. And I really enjoy it.
Prof, I want to ask. My body weight is 78 Kg, when I jump from point A to point B with one step jump. Then I have been at point Z with energy 1/10 jump from point A to B. My question is ... how is this possible and can happen ....?
Actually, your writings have sparked many of my classic questions, and this is one of them. Sorry if my question makes you confused, maybe the order of the sentence is not quite right or something.
If you were my teacher 25 years ago, maybe today we are like in my question above.
Sorry, this is too long. thanks a lot Prof. hopefully you are always healthy to write articles like this. Yours sincerely. @ Jenara.
Thanks a lot for your very nice message!
Then you belong to the people I really want to see commenting. My posts are really targeting non physicists :D
I am not too sure to follow, but this is a classical mechanics problem. You motion will be dictated by the ensemble of forces acting on your body (gravity, friction of air, etc.). The rest is to solve the equation and you will get your trajectory.
And don't be afraid of long comments: I write long posts :D
Nice post!
Have you used the equation ? i think much of the problems with it gets really clear when you start modelling. Even then 1D and 2D models of THE wave equations use theoretical boundaries like a wall of infinite difference in potency. This when constructed in reality gives rise to i.e QTE, quantum tunnel effect, giving the wave a chance to exist outside the model proving it weak.
When we model carbon chains or chromophores etc we have to add a/2 meaning half a binding length at each end of the molecule for the wave model not to spread beyond the molecule, proving it weak again and hard to use!
All theese applicable models are only build upon classical physics introducing a reoccurring pattern by adding a wave function to solve problems with values in classical models as inputs goes to infinity.
Many of the interesting aspects of the wave equation reveals it self upon usage and many weaknesses.
In short this is just another equation giving rise to different models with more precision but still clear flaws.
Was modelling orbitals and molecules earlier and it got me thinking a bit about this problem, that no physics can prove the existence of anything, only repeat experiments and apply simple models out of repetition. Then new inputs are found proving older models incorrect. Will it ever end := ) ?
Yes I did. I learned Schrodinger equation long ago, taught it more recently, and produce pedagogical material on the topic very very recently ^^
I am not sure to follow the 'flaws' you are mentioning. Do you mind elaborating? However, if you are non relativistic, the only problem is really the Hamiltonian. Once the hamiltonian is settled, the rest follows (assuming we can solve the equation). Getting better and better hamiltonian is somehow a field in itself.
cool its a intresting topic to learn indeed!
The flaws are not in the the wave equation its when applying it to any mechanical model, solving the equation, yes. The model tends to be 100 % precise only in theory, since it requires theoretical limits which we can´t set up in labs giving rise to e.g QET ?
When doing a simple model of a carbon chain molecule in 3D we must add binding lengths which does not exist! only for the electrons not to be partially located outside the molecule we are modelling :) doing this gives the best model of a molecule but its still weak that´s all :)
Thanks. I must admit that I do not know anything about quantum engineering. But from what you say, the problem is not really the equation itself but our failure in managing to correctly model reality. It is probably not trivial (possibly even not possible today) to incorporate all relevant and realistic effects from the perfect world describe by Schrodinger equation. Am I correct?
Yeah exactly.
So sad, schrodinger equation wasn’t mentioned throughout my stay in the college
Well, I guess it’s not too late to learn a few things about it. Thanks for sharing sir
It probably depends on what you studied :)
It is impressive how this equation changed the physics completely, and that at present it is still used in practically everything, when I saw my quantum mechanics course I had a lot of fun developing these equations, it is nice to remember they were good times.
And I am very happy that you are back friend and I hope you have a happy Christmas :D @lemouth
Yep, quantum mechanics made a revolution in the way we understand out world!
Merry Xmas to you too!
Without quantum mechanics our world would be a big vacuum!
or at least not understood as well :)
Schrodinger derived his equation using classical mechanics. At what point does the equations of classical physics start crumbling? When having value of gravity as infinite?
What do you mean exactly? Can you specify? Do you mean, the boundary between the classical and the quantum case?
At this level, gravity is irrelevant (fundamental particles are very light).
Yes where is the boundary between them and what defines that boundary?
What is important is to evaluate the magnitude of a typical action (the physics action) and compares it to the Planck constant. If the latter is negligible, a classical description would work.
Thanks for the answer :) I am going to look more deeply on the Planck constant and understand the consequences.
Apart from being the smallest quantity/measurement and using it in equations during college, I know nothing about it :)
it is used a lot in the equations behind many applications used in real life (I mean, beyond textbooks). But no one tells it ;)
I will read on this and get back to you in case of further questions :)
Hi, @lemouth!
I congratulate you for the pedagogy with which you present the Schrödinger equation. I really liked the way you develop the ideas to get to the equation.
Thank you for contributing to the divulgation of Physics in such a fresh way!
Thanks a lot for your nice message. It is pleasant to read :)
Hello @lemouth
You really took your time to break this down... Pure physics handles in a way even a layman could understand it. However, what I didn't understand or know is the application of this SCHRODINGER EQUATION, can you give us some instances in layman's perspective?
Upv by @eurogee, the Steemivangelist and the founder of @euronation Newbie's Support Team
For the applications, in short, anything that has quantum in it is driven by this equation, somehow.
For instance, quantum tunneling miscroscope, to name one of the most famous applications. But you have many others (quantum communications, etc.).
Ohh for real
Totally!
This is really good post . nice to read but i am confused a bit when you wrote the wave equation is it the derivative of wave or wave function, cause i think that is two different thing please explain me cause i am undergraduate student . I am new in steemit i cant figure out how to write equations through editor and put the photo on side like you . It really looks amazing. I am learning a lot by your writing skill. i hope you can give me some advice with that. i would be really happy if you read my article and give me some suggestion.
cause i dont usually get upvote from steemstem people, is something wrong with my writing
https://steemit.com/steemstem/@rifkan/what-is-universe-hiding-behind-the-darkness-is-there-a-mystery @lemouth
The wave is a function that depends on both the time and the space. The wave equation is a differential equation whose solution is the wave. Is it clearer?
Concerning the style, I use the < div > environment to align the picture to the left and to the right.
I have read your post. Please add references. I am sure this will bring you much more upvotes :D The post may also be a bit long for many people (but for me it is ok).
Now i understood the concept of there
Wave equation.Thanks for the advice. It will help me a lot.
You are welcome! Do not hesitate asking for more questions, if needed :)
Merci pour cette longue série d'articles aussi intéressant les uns que les autres !
Vivement le prochain ;)
Avec plaisir. Il y a un livre en francais que je peux recommender si le sujet t'interesse :)
You explain these breakthrough concepts very well.
It's truly amazing how one unknown scientist looks at the same equations that many others have looked at, but comes up with a world changing idea that no one saw before. Hopefully a new world changing idea can get past the peer reviewers that sometimes reject novel approaches by unknown researchers. (Example: de Broglie)
It's interesting that an object or elementary particle with velocity = 0 should have a wavelength larger than the universe.
Any object or elementary particle can have a certain wavelength, of say 1 mm, because wavelength is inversely proportional to it's momentum.
𝝀 = h/p
How close are researchers to actually measuring the ultra high frequency of electrons and/or other particles?
frequency = f = mc2/h when v = 0
and
f = pc2/hv when v > 0
The wave would then be a straight line. However, it is not possible to totally freeze a particle, so that it will never be at rest. (and in fact, you get into issues with Heisenberg here :p)
I don't know this, I am sorry. And I can't find anything satisfactory on the net (at least at 1:20 AM).
Thanks for your reply.
"The wave would then be a straight line."
Why would the line be straight? It appears that the matter wave of an electron wraps around in the orbitals of atoms. The matter wave would be in the direction the particle travels.
While the wavelength of a matter wave is independent of electric charge, it's path should be influenced by electric charge
In the double slit experiment, the size of a matter wave must be large enough to have some part of it go through both slits when an electron goes through one of the slits.
Two particles traveling parallel at the same velocity would appear to each other to have infinite wavelengths, but would still have constant frequencies.
I think you are playing with many particles like that at LHD, yes?
I indeed thought too fast and was focusing on the 1D case. With a period being infinite, we can see the 1D wave as a straight line. Which is what I had actually in mind.
The wave vector follows the momentum, or vice versa. So yes, somehow.
There is actually no way to answer that question. The electron passes through both slits at the same time. You may want to check some of the older posts I wrote on this.
Here you also need field theory and relativistic mechanics, but yes we do :)
Thanks
nice work
Pasting links to your blog as a comment like this is actually kind of spammy (especially if you do it as a comment to many many posts). Believe me, some don't like it on steemit.
In order to get our attention, just write nice posts. It is enough and we will find them :)
thankx
It is refreshing to see some Physics here on Steemit. Nice post! You can also illustrate the significance of this equation and how it led to more advanced findings.
I could, maybe in the future posts :)
The Schrodinger equation (SE), in my opinion, is the most important milestone in quantum mechanics. Before the Schrodinger equation, quantum mechanics was not really "quantum." The methods developed by Einstein, de Broglie, et. al. were more semiclassical.
However, even though it is very powerful, SE was incomplete. It mapped the change of momentum and position of a single particle through time and cannot account for dissipation. But I digress.
Your post is wonderful. I often struggle communicating quantum mechanics to other people and this post gave me insights on how I can help my friends who come from non-physics disciplines appreciate the beauty of quantum mechanics.
Thank you for this!
You are welcome. Thanks for your comment by the way.
I am trying to put things simply enough so that anyone can understand. However, at some point we need to rely on equations and this is where we start to lose people, in general :)
I didn't want to enter few-body systems here... Way off topic for a blog I guess :D