Ciencia Matemática: Factorización Método Resolvente.
Buenas noches queridos estudiantes y amantes de la ciencia Matemática.

<centerZ
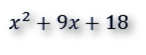
Primer paso identificar los términos:
a=1
b=9
c=18
Sustituimos seguidamente en nuestra fórmula:

Continuando con el tema de factorización, específicamente factorización de trinomios, resolveremos el mismo ejercicio propuesto en el (Método Ensayo y Error)
Método Resolvente
Este método se aplica mediante la siguiente fórmula cuadrática:

<centerZ
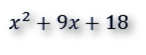
Primer paso identificar los términos:
a=1
b=9
c=18
Sustituimos seguidamente en nuestra fórmula:

Efectuamos las operaciones:




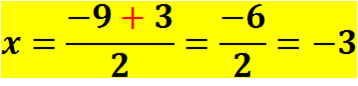


Gracias @provenezuela
Usa el #entropia. Una comunidad que apoya el contenido en español promoviendo el contenido de calidad.


Únete a Redfish Power UP League and Wall of Fame. (Aquí)
9.9 = 81
4.1.18=72
2.1=2

81-72=9

Calculamos la raíz cuadrada de 9 y nos queda:

Vamos a encontrar el valor de x de la siguiente manera, una expresión con el signo positivo y la otra con el signo negativo:


Resolviendo:
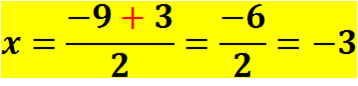
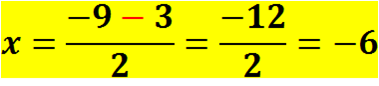
Entonces despejando:


El resultado de la factorización del ejercicio es:
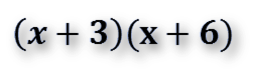
Nos encontramos con otro ejemplo en la próxima publicación.
Nos vemos pronto con otro ejercicio. Cómo podrás ver, la práctica es importante, y no debemos temer, la matemática es bella una vez que decidimos estudiarla como se debe.

Gracias @provenezuela
Usa el #entropia. Una comunidad que apoya el contenido en español promoviendo el contenido de calidad.


Únete a Redfish Power UP League and Wall of Fame. (Aquí)
0
0
0.000
congrats. Very well explained :)
Hi!!! thank you for reading!
¡Felicitaciones!
Estás participando para optar a la mención especial que se efectuará el domingo 9 de febrero del 2020 a las 8:00 pm (hora de Venezuela), gracias a la cual el autor del artículo seleccionado recibirá la cantidad de 1 STEEM transferida a su cuenta.
¡También has recibido 1 ENTROKEN! El token del PROYECTO ENTROPÍA impulsado por la plataforma Steem-Engine.
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Contáctanos en Discord.
Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Hola amiga, muy importante los métodos de factorización para encontrar la solución de ecuaciones polinómicas de orden superior, sobre todo considerando que para abordar las matemáticas a nivel universitario nuestros jovenes estan llegando muy mal preparados en estas bases fundamentales.
Para el caso de la ecuación de 2º grado que tu ejemplifican muy bien en este post, también se puede factorizar por el método del trinomio cuadrado perfecto, en el que se buscan dos números (x + )(x -) que multiplicados den el factor [c] y que sumados algebraicamente nos de el factor [b], por lo que según esta teoría estos números sería 3 y 6, ya que multiplicados (6x3)=18 el cual nos daría el factor término independiente de la ecuación de segundo grado [c] y sumado (6+3)=9 nos daría igual al valor del término [b], por lo que finalmente la factorización daría lo que tu expresas en este artículo:
(x+3)(x+6). Sin embargo está muy bien explicado el como usar la ecuación de la resolvente, ya que si la ecuación de segundo grado no es un trinomio cuadrado perfecto entonces se tiene que factorizar obligatoriamente por la ecuación de la resolvente.
Saludos @isgledysduarte, gracias por compartir este método de factorización, esperando con ansias ver más de tus publicaciones.
Hola!! uenas tardes @carlos84 gracias por tomar tu tiempo y leer. Gracias por tu aliento, seguiré publicando y estaré encancatada que nos compartas tus aportes!
Exactamente son métodos para resolver trinomios y no tos se pueden factorizar por el método del trinomio cuadrado perfecto por eso recurrimos a otroa métodos. En el siguiente trabajaremos con Ruffini
Que bueno estare atento, sigue adelante buen trabajo, no desmayes, saludos.