La Programación Lineal en la Identificación de Problemas en la Toma de Decisiones Parte III
Bienvenidos Estimados Amigos:
Siempre parto de la idea que la representación gráfica te permite tener mayor visualización del estudio o problema. Para iniciar se debe representar cada una de las restricciones para calcular el máximo o el mínimo de una función, será suficiente con solo evaluar la función objetivo en todos los vértices y encontrar en la medida de lo posible la solución factible, comúnmente en uno de sus vértices se encuentra la mejor respuesta (solución óptima) para el beneficio, crecimiento y la rentabilidad de la empresa respectivamente.

A continuación voy a mostrar un compendio de ejercicios de Programación Lineal a través del método gráfico:
Caso Practico N° 1:
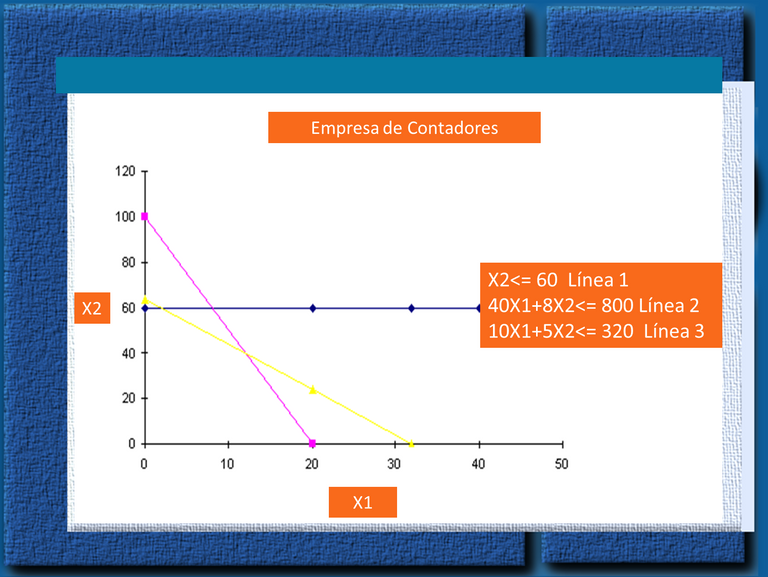
Una Empresa de Contabilidad se dedica en realizar certificados de Ingresos y declaración de Impuestos Sobre la Renta. El dueño tiene principal interés en saber cuántas declaraciones de impuestos sobre la renta y certificados de Ingresos pueden realizar mensualmente para lograr la maximización de sus ingresos. Actualmente dispone de 800 horas de trabajo directo y 320 horas para hacer la respectiva investigación. Un certificado de ingreso en promedio requiere de 40 horas de trabajo directo y 10 horas para su revisión. Asimismo aporta un ingreso de 300. Una Declaración de impuesto requiere de 8 horas de trabajo directo y de 5 horas de revisión, la cual produce un ingreso de 100. El máximo de certificados de ingresos mensuales disponibles es de 60.
La principal pregunta del problema es maximizar el ingreso total. Ahora procedemos a la selección de las variables de decisión:
Cantidad de declaración de impuestos sobre la renta (X1).
Cantidad de certificados de ingresos (X2).
Maximizar
Z= 300X1+100X2
Sujeto a:
Ahora vamos a conformar las ecuaciones con las restricciones que nos señala el problema:
- Tiempo utilizable de trabajo directo
- Tiempo utilizable de revisión
- Número máximo de certificados de ingresos.
40X1+8X2 < 800
10X1+5X2< 320
X2< 60
La de no negatividad:
X1,X2> 0
Continuando con el problema, en este procedimiento se analizan los valores en la función objetivo. El vértice que representa el mejor valor de la función objetivo será la solución óptima. Como es de conocimiento la solución óptima siempre se encuentra en uno de los vértices del conjunto de soluciones factibles. Para iniciar con el trazado de las restricciones debo igualar las mismas a 0, Voy Sustituyendo valores, es decir X1, X2 en la Función Objetivo, de esta manera podemos mediante despeje de las ecuaciones iniciar con la tabulación que nos arrojara las coordenadas (X, Y) para plasmar cada una de las líneas gráficas. Como vamos a graficar en el plano cartesiano es necesario renombrar las variables
Igualamos restricciones:
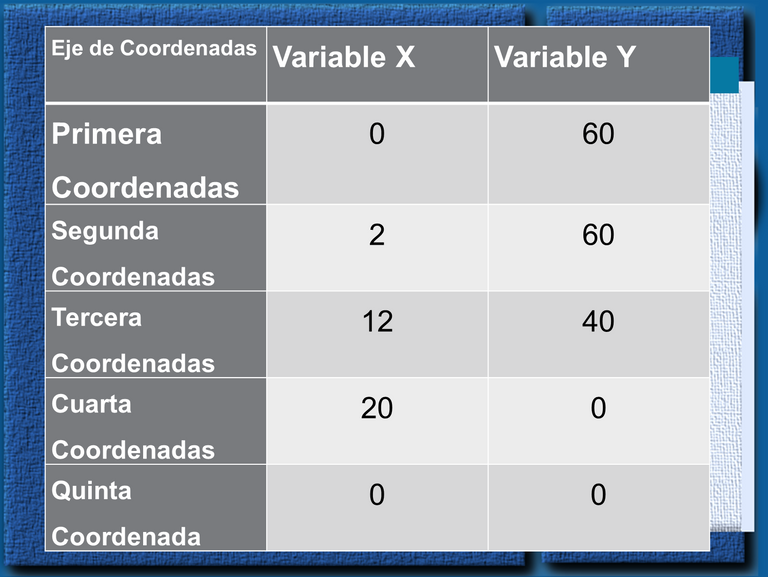
Con la primera restricción, hallamos las primeras dos coordenadas y asi sucesivamente cada vez que vamos sustituyendo los valores en la función objetivo, para hallar las coordenadas regularmente debemos llevar a unas de las variables a cero, para que se me haga más fácil despejar la segunda variable.
(X1,X2) Z= 300X1+100X2
(0,60) Z=300(0)+100(60)
Z= 0+6000 Z= 6000
(2,60) Z= 300(2)+100(60)
Z= 600+6000 Z= 6600
(12,40)= Z= 300(12)+100(40)
Z= 3600+ 4000 Z= 7600
(20,0) Z= 300(20) +100(0)
Z= 6000+0 Z= 6000
(0,0)= Z= 300(0)+100(0)
Z=0
Solución Óptima o Solución Visual se encuentra:
X1= 12 Declaración de Impuestos Sobre la Renta
X2= 40 Certificado de Ingresos
Z= 7600 es donde se Maximiza los Ingresos.
Ahora procedemos a graficar para tener una mayor visualización del Valor Optimo. Lo más importante de este método es el juicio para interpretar correctamente las variables para detectar los puntos fuertes o débiles de la empresa, también para determinar si existen probables incoherencias entre las ganancias, los gastos y en la disponibilidad del tiempo para poder obtener resultados satisfactorios, eligiendo la mejor alternativa dependiendo de las herramientas y los conocimientos matemáticos, y así dar cumplimiento con el objetivo principal de saber a ciencia cierta cuántas declaraciones de impuestos sobre la renta y certificados de Ingresos pueden realizar mensualmente la empresa de contadores para lograr la maximización de los ingresos.
Ustedes se preguntara porque la variable x y y nos da la función Objetivo de 7600, porque esa fue la que seleccionamos: Sin embargo, el método de búsqueda de la Solución Óptima es el de iteración por vértice, y que consiste en hallar todas las coordenadas de los vértices y en cada coordenada se evalúa la función objetivo, es decir que en cada coordenada nos proporciona un valor x y otro y luego sustituimos estos valores en la Función Objetivo Z= 300X1+100X2 y luego evaluamos los resultados seleccionando la mayor cantidad. En conclusión para finalizar con esta parte del método grafico se recorre la región factible con rectas paralelas a la que hemos representado, que se conocen normalmente como líneas de nivel.
Se observa cómo va variando la función objetivo al desplazar las rectas de nivel en un sentido o en otro y en los últimos puntos de contacto con estas rectas es donde se proporcionan el valor máximo y mínimo.
Vamos a obterner las variables o Coordenadas:
En el método grafico existe una variedad de problemas que es importante estudiar porque no en todos los casos se presenta una solución óptima única. Ahora procedemos a ver los diferentes problemas:
Solución Óptima Múltiple:
En los problemas de programación Lineal, consiste en la búsqueda de una solución óptima, pero existen casos donde la función objetivo es exactamente igual, en estos casos se debe realizar un análisis de sensibilidad, es decir se procede al estudio del comportamiento del consumo de los recursos y limitaciones, evidentemente donde prevalece el constructo de rendimiento de los recursos más limitados y costosos.
Caso Practico N° 2
Empresa Sebastián ha recibido una gran cantidad de partes prefabricadas para la elaboración de juegos de comedor, los juegos son de dos modelos A y B, y estas no requieren más que ser ensambladas y pintados. Este mes se ha determinado dedicar 10 horas para el ensamblado y 8 de pintura para elaborar la mayor cantidad de juegos de comedor posibles teniendo en cuenta que cada comedor del Modelo A requiere de 2 horas de ensamblé y 1 de pintura. Y el modelo B 1 hora ensamble y 2 de pintura. Si la utilidad es de Bs 20000 por cada comedor del Modelo A y Bs 10000 del B. Determinar el modelo adecuado de producción.
Las Variables de Decisión:
X = Cantidad de Juegos de Comedor del Modelo A
Y= Cantidad de Juegos de Comedor del Modelo B
Función Objetivo:
Z max =20000x+10000
Restricciones:
2x+y <0 = 10 Horas ensamble
X+2Y<o = 8 Horas pintura
X,y >o = 0 No Negatividad
Z(0)= 20000(0)+10000(0)= 0
Sustituimos las variables en la Función Objetivo :
Coordenada A
Z= 20000(0)+10000(4) = 40000Bs
Coordenada B
ZB= 20000(4)+10000(2)= 10000 Bs
Coordenada C
ZC =20000(5)+10000(0)=10000Bs
Existen Dos Soluciones Optimas
X=4 yY=2
X=5 y Y=0
¿Cuál decisión tomar antes dos soluciones óptimas?. Vamos a visualizar el grafico para observar y seleccionar la mejor alternativa.
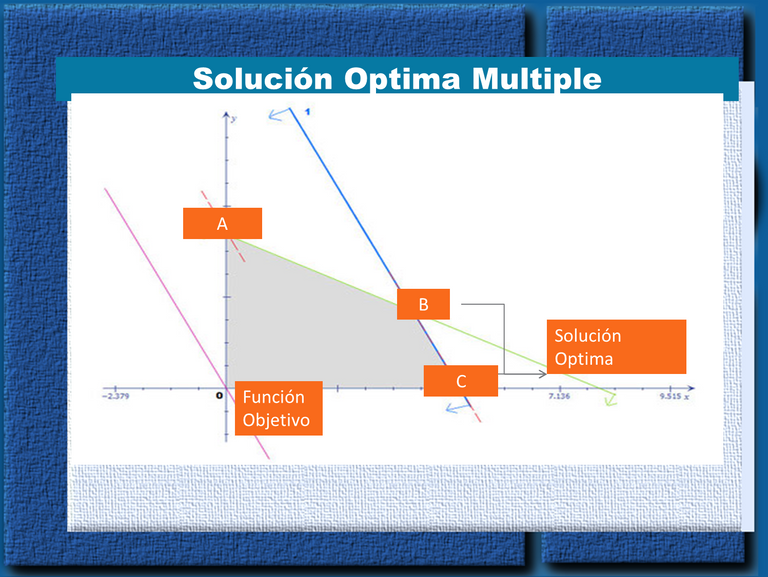
Es aquí donde se pone en juego la capacidad de la persona que debe tomar las decisiones porque debe ser muy analítico y saber cuál es la mejor opción tomando en cuenta varios elementos como el consumo distinto de determinados recursos como las horas que se lleva en ensamble y en pintura, adicional a ello otros factores externos como el sitio donde se almacena los juegos de comedores, dado que existe una alternativa donde se elaboran más comedores que en la otra.
Observación:
Las imágenes fueron realizadas en el Programa de Microsoft Power Point por mi autoría
Referencias:
- Gabaldón, Fernando. (2003) Técnicas de Negociación. Primera Edición. Editorial IMMECA.
- Gomollon, Felix (1996) Ejercicios de Investigación de Operaciones. Madrid. Editorial ESIC.
- Fedossova, Alina y Buitrago, Oscar. (2011). Introducción a la Programación Lineal con Administración de Operaciones. Bogotá. Editorial CESA.
Los invito a leer contenidos de ciencias, matemáticas, ingeniería, tecnología y salud visitando la etiqueta #Stem-espanol, a su vez unirse al canal de discord https://discord.gg/djk49A, donde los días jueves a las 8 pm Hora de Venezuela podrás participar en los conservatorios.
Lcda. Exqueila Rodriguez Diaz
Especialista en Derecho Mercantil Mención Talento Humano
Egresada de la Universidad de los Andes
Especialista en Derecho Mercantil Mención Talento Humano
Egresada de la Universidad de los Andes
$rewarding 100% 15 min
¡Saludos! Tu post ha sido votado y ha tenido resteem por el proyecto @votomasivo.
Apreciación: Muy interesante post para quienes se especialicen en el área, es un gran aporte para la comunidad de @steemit felicidades!
Para recibir más votos de @votomasivo te recomiendo que comiences a usar el tag "neoxian", así podrás obtener recompensas en Steem y en NEOXAG.
Los posts con esta etiqueta tendrán prioridad en nuestra curación.
Para más información sobre este tema:
https://steemit.com/neoxian/@votomasivo/votomasivo-se-une-a-neoxian-city-update-or-version-en-esp
Curado por @fulani
¡No olvides invitar a tus amigos a unirse a nuestro trail de curación para apoyar post de calidad!
También puedes apoyanos uniéndote a nuestro fan base y delegándonos Steem Power. ↓
Sé parte de nuestra comunidad en Discord