NEWTON’S LAWS AT WORK: Joule’s Experiment on Heat and The Gravitational Potential Energy In The Earth’s Field.
Experience tells us that, when work is done on an object, energy can be transferred to make it hotter. Hitting metal with a hammer is an example. Conversely, we can use a substance that is hotter than its surroundings to do work, such as burning petrol in a car engine.

In the nineteenth century, the debate was over whether ‘heat was a form of energy’. We now say that ‘an energy input is required to make something hot, and an object hotter than its surroundings can be used to do work’.
James Prescott Joule (1818-1889) was an amateur scientist interested in heat and energy. Between 1843 and 1878, he carried out very careful experiments to establish the principle of the conservation of energy as it applied to heating and working. He set out to show that, when frictional forces do work on a substance, it gets hotter, and that there is a direct relationship between the work done and the rise in temperature of the substance.
In his experiments, Joule measured the work done in stirring some water and the rise in temperature it produced. A paddle-wheel, which was driven by a falling weight, rotated in the water – doing work via friction on the water and heating it at the same time. Joule shows that the work done to lift the weight up to the starting position was always proportional to the ‘heat energy gained by the water as the weight fell.
At that time, ‘heat’ was measured not in joules but in calories, a unit still used on food packaging today. We now remember the work of Joule by the unit of energy named after him.
The principle of conservation of energy – that energy cannot be created or destroyed – is now thought of as one of the most fundamental laws of the material world. It has been extended by Albert Einstein to include the idea that mass is a form of energy.
ENERGY CONSERVATION IN A UNIFORM GRAVITATIONAL FIELD
As we have seen, gravitational potential energy is measured simply as the work done to move an object directly against the force of a gravitational field, that is, upwards. So,
change in gravitational potential energy = work done when moving something against a gravitational force
ΔE = gravitational force × distance moved
ΔE = mgΔh
This formula for a change in gravitational potential energy is correct only if the value of g, the gravitational field strength is constant over the whole distance Δh. The formula is accurate enough for objects moving close to the surface of the Earth, but will not be correct for distances comparable with the size of the Earth, let alone distances on the scale of the Solar System. This situation is considered more fully in the next paragraph.
So far in my last post and the previous, I have been able to solve some dynamic and kinematic problems using the ideas of force, mass, acceleration and the equations of motion. These techniques are easy to use when forces on objects are uniform and produce uniform accelerations of the objects. But in most everyday situations, things aren’t so simple, and it is often more convenient to solve problems using the idea of the conservation of energy, as in the following Example.
EXAMPLE
A holiday park has a roller coaster as shown in the diagram below. The ride follows a loop path that begins and ends at D. The car is hauled from D to point A, the top of the ride, and then moves from rest, under gravity, to arrive at point D again.
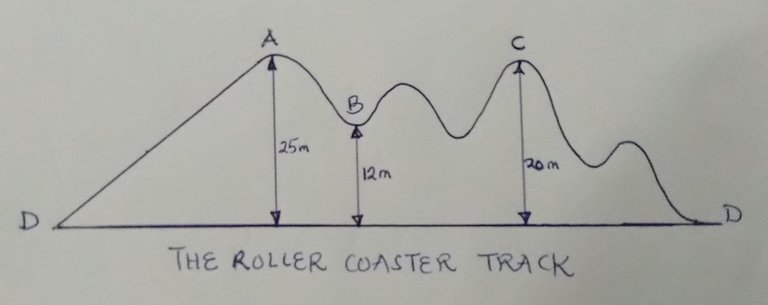
A diagram of a roller coaster track drawn by me
a. Ignoring frictional forces, what are the speeds of the car at: point B; point C; point D?
b. To stop at point D, the car has to be braked from a speed of 10 m/s. In practice, friction has reduced the car’s speed during the ride. By point D, what proportion of the energy which the car had at point A has it lost because of friction?
ANSWER
a. The whole of this part is solved using the principle of the conservation of energy – we can just look at the changes in potential energy and kinetic energy at the various points. We do not need to know how the force varies at different points on the track. We don’t even need to know the mass of the car, since it is the same throughout the ride, and cancels out, as we can see in the first solution.
Speed at point B
Gain in kinetic energy = loss in potential energy
½ mv2 = mgΔh (where g = 9.8 m/s2)
v2 = 2gΔh (where Δh = 25 - 12 = 13, in metres)
v2 = 2 × 9.8 × 13 = 254.8 m2 s-2
giving: v = 16 ms-1
Speed at point C
The net loss in potential energy at point C is due to a drop of 5 m from point A. Check for yourself that the speed at point C is just under 10 m/s.
Speed at point D
The drop is 25 m.
So, using v2 = 2gΔh,
v2 = 2 × 9.8 × 25 m2 s-2
v = 22 m/s
b. Before braking, the car is travelling at 10 m/s. So, before braking, the kinetic energy ½ v2 per unit mass (m = 1 kg) is:
0.5 × 102 = 50 J kg-1
For a theoretical value for the car’s kinetic energy we assume that the ride is frictionless, so the gain in kinetic energy per unit mass equals the potential energy, mgΔh, lost per unit mass:
9.8 × 25 × 245 = J kg-1
So the energy wastage due to friction per unit mass of car is:
245 - 50 = 195 J kg-1
The proportion of energy wasted during the ride
= 195 × (245)½ = 0.80 or 80 %
GRAVITATIONAL POTENTIAL ENERGY IN THE EARTH’S FIELD
The gravitational field strength of an object varies with the distance from that object, and the field strength obeys the inverse square law. Earth has a radial gravitational field. Over short distances close to the Earth’s surface, the variation in gravitational field strength is too small to worry about, so here we assume that the field is uniform.
The table below summarises the relevant formulae. G is the universal gravitational constant and M is the mass of the Earth. Some of the formulae still need to be explained.
Calculating the gravitational field strength
| Uniform field | Radial field | |
| Force | F = mg | F = -GMm/r2 |
| Change in gravitational potential energy | mgΔh | GMm (1/r1 – 1/r2) |
| Gravitational potential | (not a useful idea in a uniform field) | -GM/r |
The universal gravitational constant G = 6.67 ×
10-11 Nm2kg-2. The Earth’s mass M = 5.98 × 1024
kg.
‘NEGATIVE ENERGY’ A VERY USEFUL IDEA
Before looking at the details of the radial field, we have to clear up a matter which often causes confusion – the negative sign given to the value of gravitational potential energy.
Imagine an object of mass m in empty space an infinite distance r, from any other massive body. Force in a radial field is GMm/r. But since r, is at infinity, the object will have zero force acting on it. It cannot ‘fall’ towards anything, so it has no potential energy and it cannot gain kinetic energy – or do any work. So it must have zero gravitational potential energy.
Now imagine the same mass m sitting on the Earth. To move it to infinity (beyond the gravitational field of the Earth or any other body). You would have to give it energy – kinetic energy if you propelled it in a rocket. (Soon, I shall calculate just how much energy it needs.) But when the mass gets back to infinity again, it will, of course, have zero gravitational potential energy.
The only way to ‘balance the books’ (and so conserve energy) is to accept that when the mass rested on the Earth it had negative energy, and that it needed the same quantity of positive energy to reach infinity and stop there (with zero energy):
Some positive kinetic energy + same amount of negative potential energy = zero energy
FINDING A VALUE FOR GRAVITATIONAL POTENTIAL ENERGY IN A RADIAL FIELD
An object of mass m is at a point r2 from the centre of the Earth. Then it is moved to a nearby point r1, a small extra distance Δr closer to the Earth's centre. For a small movement, the force does not vary within distance Δr. The object is, for all practical purposes, in a uniform field. So the change in gravitational potential energy would simply be mgΔr. The change in potential energy per unit mass is gΔr, and is represented by the area ABCD under the graph.
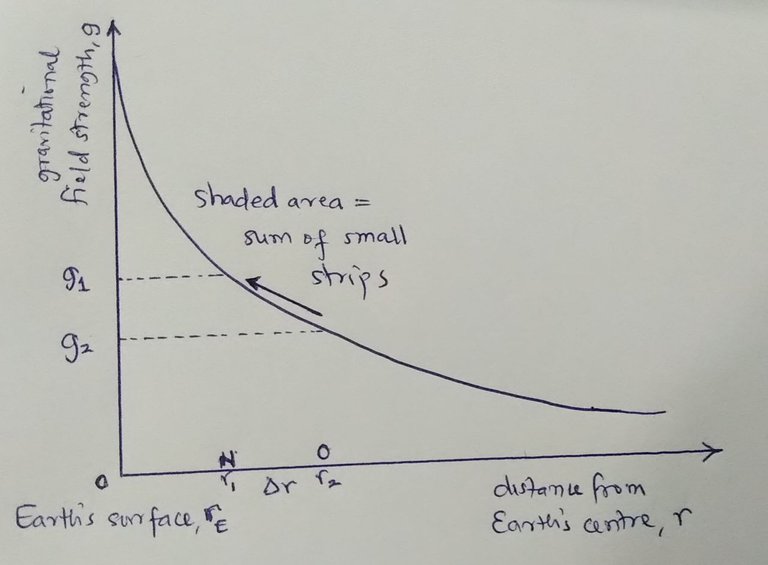
A diagram drawn by me
The curved graph above represents a field of varying strength, getting less as the distance from the Earth increases. So, as the object is moved from r2 to r1, it experiences an increasing gravitational force. The change in potential energy per unit mass is represented by the area NOPQ under the graph. In algebraic terms this works out to be E = GM (1/r1 – 1/r2). See the paragraph below for this.
Calculating the Change in Gravitational Potential Energy Graphically and Numerically
We can find the value of the change in gravitational potential energy from the graph shown above by counting the squares in each small shaded strip. This is tedious! Instead, we can add them up numerically using a spreadsheet.
ALGEBRAICALLY, USING CALCULUS
We can find area NOPQ in the figure more easily using a simple formula for the result. We employ calculus to get the formula, recognizing the fact that, for large distances, g depends upon r according to the inverse square law. The symbol Ep is used for gravitational potential energy.
The change in gravitational potential energy, ΔEp is given by using the definition of work (force × distance). The potential energy gained equals the work done in moving mass m, a distance Δr between points at distances r2 and r1 from the centre of the Earth.
So: ΔEp = -GMmΔr / r2
As explained earlier, the negative sign is there to balance the books and keep potential energy negative. The equation may be integrated to give:
Ep = -GMm∫ 1/r2 dr = GM(1/r2 – 1/r1) which is usually written as: Ep = GMm/r2 - GMm/r1.
This is the potential energy difference formula, where Ep is the difference in potential energy for a mass m at a point at distance r2 from that for the same mass at distance r1 from the centre of the Earth. If the object falls freely it equals the kinetic energy gained.
EXAMPLE
THE ENERGY GAINED BY AN ASTEROID FALLING TO EARTH
Estimate a value for the kinetic energy of an asteroid colliding with the Earth.
ANSWER: Assume that the asteroid has a diameter of 10 km and is made of rock of density 3000 kg per Cubic metre. This gives it a mass of about 1.6 × 1015 kg.
Assume, too, that it falls from infinity, that is, from a place where the gravitational potential is zero. At the Earth's surface it is at a place with a gravitational potential of -GM/rE. In other words, its potential energy per kilogram has been reduced by GM/rE.
Loss in gravitational potential (energy per unit mass):
-GM/Rk = - (6.7 × 10-11) (6.0 × 1024) / 6.4 × 106
= - 6.3 × 107 Jkg-1
This energy has of course been converted to kinetic energy. So the total kinetic energy of the asteroid is equal to the potential energy lost by its mass of 1.6 × 1015 kg:
gain in KE = loss in GPE (gravitational potential × mass)
= 6.3 × 107 (J kg-1) × 1.6 × 1015 (kg)
= 1.0 x 1023 J
We can calculate its impact speed from the formula for kinetic energy:
Ek = ½ mv2 = 1.0 × 1023 J
v2 = 2 × Ek/m
v = √ (2 × 1023/1.6 × 1015)
= 11.2 × 103 m/s
So the impact speed is 11.2 km/s.
I’ll be stopping here for now. Till next time, I remain my humble self, @emperorohassy.
Thanks for coming.
REFERENCES
https://www.aps.org/publications/apsnews/201506/physicshistory.cfm
https://en.wikipedia.org/wiki/Mechanical_equivalent_of_heat
https://demonstrations.wolfram.com/JoulesExperiment/
https://courses.lumenlearning.com/boundless-physics/chapter/energy-conservation/
https://opentextbc.ca/physicstestbook2/chapter/gravitational-potential-energy/
https://www.livescience.com/33129-total-energy-universe-zero.html
https://en.wikipedia.org/wiki/Negative_energy
http://www.physbot.co.uk/gravity-fields-and-potentials.html
http://astrowww.phys.uvic.ca/~tatum/celmechs/celm5.pdf
http://www.lehman.cuny.edu/faculty/anchordoqui/chapter14.pdf
http://www.physbot.co.uk/gravity-fields-and-potentials.html
https://en.wikipedia.org/wiki/Energy_level
http://zebu.uoregon.edu/disted/ph101/lec05.html
https://en.wikipedia.org/wiki/Impact_event
http://curious.astro.cornell.edu/about-us/38-our-solar-system/the-earth/impacts/51-what-would-happen-if-an-asteroid-10-kilometers-across-hit-the-earth-beginner
https://science.howstuffworks.com/nature/natural-disasters/asteroid-hits-earth.htm
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.