FLUID PRESSURE: APPLICATIONS OF BERNOULLI’S PRINCIPLE, STREAMLINING, TURBULENT FLOW AND THE DRAG EFFECTS FOR A VEHICLE.
One of the applications of Bernoulli’s principle is the fragrance spray. The diagram shows a hand-operated fragrance spray. When you press the bulb, air is forced through the tube, which has a constriction in it – that is, part of the tube is narrower than the rest. The air travels faster in the narrow part and so its pressure decreases. Liquid is drawn up the vertical tube, breaks into droplets as it meets the air jet and is carried out of the nozzle in a fine spray.
Aerofoils: the principle of flight
An aerofoil is the shaped wing of an aircraft. The top surface of an aerofoil is convex, which means that, while the aircraft is in flight, air travels faster over the top surface than over the bottom.
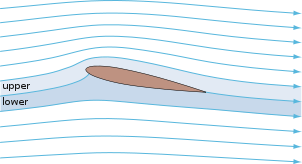
This is because the air stream has to travel a greater distance over the top surface in the same time – as with a liquid, the air mass has to be continuous. The result is a smaller pressure on the upper surface than on the lower, and the aerofoil experiences a net upward thrust – called lift. The wing is usually angled to the direction of motion so that it has to push against the air. This produces an additional force (reaction) with an upward component to add to the lift. In general, the angle the aerofoil makes with the forward direction of motion (angle of attack) is large enough for this reaction force to be more effective in maintaining height than the aerofoil’s Bernoulli effect.
STREAMLINES AND TURBULENT FLOW: FRICTION AND DRAG
The simple theory of fluid flow described above assumes that the flow is steady, so that particles of the fluid flow in smooth paths – as shown by the continuous streamlines made visible by streamers. But above a certain speed the flow becomes chaotic and we have turbulent flow. Energy is dissipated in sound and heating; and extra pressures are produced which can affect the straightforward motion of a vehicle. There is often turbulent flow when two air streams that have diverged over a moving object join together again. This effect can be seen in the air behind a car being tested in a wind tunnel. The disturbed turbulent air produces a low-pressure region, which tends to pull the car backwards, contributing to the drag forces that oppose the motion of any object through a fluid. The turbulent drag force is reduced by vehicle design. The best shape is like an aerofoil, of course, but drivers would worry if, at a certain speed, the car started flying! The rear spoiler fitted to some cars, as shown in the figure below, is a way of reducing the drag force by making the air flow less turbulent at the back of the vehicle. Racing cyclists and downhill skiers wear specially shaped helmets to reduce the effect of turbulence.

A car having a rear spoiler. Pixabay
Other drag forces act on a surface moving through a fluid. For example, air has to be pushed away as a car drives through it, and this produces a reaction force that acts on the car. Next, I will discuss the frictional forces between the vehicle’s surface and the fluid.
FRICTION AND VISCOSITY
Layers of fluids move over each other very easily; for this reason a fluid cannot resist a shearing stress. But fluids do have a kind of internal friction called viscosity. This varies: moving a knife blade through water is much easier than moving it through honey. Similarly, viscous forces arise when adjacent layers of liquid move against each other. In a simple model of what happens, we assume that when a fluid moves through a pipe the fluid layer next to the wall of the pipe is at rest, and that the fastest stream is at the centre of the pipe. There is a constant velocity gradient in the fluid, Δv/Δx, where x is the distance measured radially in the pipe. A liquid that behaves like this is called a Newtonian liquid. Friction between adjacent layers in the fluid determines how fast the fluid can flow compare – pouring water and treacle. A fluid has a coefficient of viscosity η (the Greek letter eta) which determines the size of the viscous force.
The resistive viscous force is greater for a wider pipe. These factors are combined in Newton’s law of viscosity. When F is the force due to viscosity acting on a fluid stream of cross-sectional area A, against the direction of flow, then:
F = ηA (Δv/Δx)
This force is also the drag force on the sides of the container.
Viscosity has units of Ns m-2 . Blood is thicker than water i.e blood is more viscous than water. Viscosity varies with temperature: as a general rule the coefficient decreases as temperature increases, so that liquids are more ‘runny’ when hot.
STOKES’ LAW
Viscous forces also affect the speed of streamline motion of an object in fluid. For a sphere in streamline motion at a speed v through a fluid, the Irish physicist George Stokes (1819-1903) proved that it would experience a drag force:
F = 6πηrv
Where η is the coefficient of viscosity of the fluid and r is the radius of the sphere. This idea may be linked to the terminal speed of a falling sphere. In this case the viscous drag on the sphere equals its weight:
mg = 6πηrv
EXAMPLE
Calculate the terminal speed of a) a lead sphere, b) a hailstone, both having a radius of 2 mm.
[The density of lead is 1.14 × 10 kgm-3; the density of ice is 9.2 × 102 kgm-3.]
Solution: The condition for terminal speed is that mg = 6πηrv, so terminal speed v is:
v = mg / 6πηr
The mass of the lead sphere is:
m = volume × density = 4/3 πr3 × ρ
So the equation can be simplified to:
v = 2r2ρg / 9η
= 2 × 4 × 10-6 × 1.14 × 104 × 9.8 / 9 × 1.8 × 10-5
giving:
v = 5.5 × 103 ms-1
The only difference in the conditions of the problem is the density of the materials. Thus the ratio of terminal speeds is the same as the ratio of densities. Ice is less dense than lead, so it falls more slowly.
The terminal speed of the hailstone is:
v = 5.5 × 103 × 9.2 × 102 / 1.14 × 104 = 4.4 × 102 ms-1
Note that in practice both spheres would fall more slowly, since turbulence would set in at much lower speeds.
DRAG EFFECTS FOR A VEHICLE
Energy can be ‘saved’ in transportation by reducing a variety of losses. Nowadays the drag factor is taken into account in car design. This factor indicates how much energy a moving vehicle ‘loses’ as a result of air friction. This kind of friction loss is due to the vehicle working against a frictional drag force Fd. When v is the vehicle’s speed, A its cross-sectional area and ρ the density of air, then:
Fd = ½ CA ρv2
Where C is its drag coefficient, a constant which depends upon the shape of the vehicle. The car is also subject to rolling friction, due to the contact of the tyres with the road surface. This creates a force given by μN where N is the normal reaction between car and road. The coefficient of rolling friction for a car is about 0.02. The normal reaction N gets slightly less at higher speeds as the car behaves like an aerofoil (luckily not very successfully at usual road speeds).
Rolling friction is much more important than drag for a car travelling at low speeds. However, drag increases as the square of the speed. Drag and rolling friction become equal at a speed of about 18 ms-1 (40 mph) for a typical car, and eventually drag is the main source of frictional loss.
The main energy losses from a car engine are not due to these effects at all. Heat engines are inefficient, and dissipate almost 70 per cent of the energy that comes from the burning fuel. There are other friction losses in the transmission, so that the energy available for moving the car is only about 14 per cent of the energy supplied by the fuel.
EXAMPLE
How much power needs to be delivered to the wheels of a car travelling at a typical motorway speed of 31 ms-1 (70 mph)?
(Data: At this speed, rolling friction provides a force of 210 N; the car has a cross-sectional area of 1.8 m2; the density of air is 1.3 kg m-3; the drag coefficient of the car is 0.4.)
SOLUTION: The drag force on the car is Calculated from:
Fd = ½ CA ρv2
= 0.5 × 0.4 × 1.8 × 1.3 × (31)2 N = 450 N
Drag force = 450 N. Thus the total frictional force on the car is:
210 N + 450 N = 600 N
This force does work that requires energy to be supplied by the car’s engine.
The work done per second = force × distance moved per second (speed)
that is: Power needed = work done per second = frictional force × speed
= 660 N × 31 ms-1 = 20.5 kW
HOW FAST CAN A VEHICLE GO?
The speed of a train or a car – or a cyclist – is the result of a battle between the driving force and resistive forces. Newton’s laws act as the referee. The best way to tackle many problems is from the point of view of energy and power (the rate of transferring energy).
The car in the figure below is travelling on a horizontal road at a steady speed of 25 m/s with its engine delivering energy at its maximum rate of 14 kW. What is this energy being used to do? It is, in fact being used to do work against friction forces: inside the engine, the transmission, the wheels and – mostly – against the forces of drag and viscous air friction.

It is also pushing air out of its way and giving it some kinetic energy. The car is not accelerating or going uphill so doesn’t gain potential or kinetic energy. Suppose the total of the friction and other forces opposing motion is F. When the car travels 25 metres it does work of 25F.
The car takes one second to travel 25 metres, so the work done per second is also 25F. This is the power developed by the engine of course, since all of it is being used to do work against friction.
So, 25F = 14 kW in this case. This gives the total frictional force as 560 N i.e 14000 / 25.
The power generated by the engine is P. What I have shown is that when the car is travelling at a steady speed on the flat
power = frictional forces × speed
P = Fv
Going uphill
Suppose our car is now climbing a not very steep hill that rises 1 metre for every 25 metres along the road. Some of the power from the engine has to lift the car uphill and so give it potential energy. The car can’t go as fast, because the engine has an extra task:
P = Fv + mg Δh
Here, Δh is the increase in height of the car every second. This depends on the angle of slope and the speed of the car: Δh = v sin θ which shows that this is simply v/25 in this example.
The car’s speed drops:
Fv + mg Δh = P
(F + mg/25) v = P
If the car’s mass is 800 kg and if (not too likely) F stays the same at 560 N, then you should be able to check that the car’s speed drops to just under 16 ms-1.
FREE-BODY DIAGRAMS
A good way to test your understanding of what is happening when bodies are acted upon by forces is to draw a simple diagram showing where and in which direction the forces act.
 Free Body Diagram. AndrewDressel at English Wikipedia, CC BY-SA 3.0
Free Body Diagram. AndrewDressel at English Wikipedia, CC BY-SA 3.0
To do this you need to have a good understanding of Newton’s laws of motion and be able to apply them to the situation the body finds itself in. For most everyday situations the forces acting will be caused by gravity (or some other applied force), friction and any force of contact between the object and another object. This contact force is often called a reaction force – but this can be a confusing name because it may not be the same force as that discussed above in connection with Newton’s third law. The figure below shows some simple situations with the forces involved drawn as vectors from the points where they act.
CONCLUSION
After reading all these series of posts starting from NEWTON ON THE MOVE: Going Around the Bend, Practical Applications of Collisions, Fluid Pressure and this, you should have improved your understanding of Newton’s laws of motion as applied to transport and moving fluids. You should have also understood the role of friction in transportation, ability to apply the laws of static and sliding friction and coefficient of friction. I also mentioned about the ideas of viscosity, streamline flow and drag factor, and relating them to Stokes’ law and terminal speed. I discussed the physics of rotating bodies and used the ideas of angular velocity, angular acceleration, torque, rotational inertia and rotational kinetic energy.
I demonstrated how to apply the laws of conservation of momentum and conservation of energy as appropriate to elastic and inelastic collisions. The concept of pressure in fluids and relating it to practical situations involving hydraulics and flotation. The Archimedes’ principle and the applications of Bernoulli’s principle to explain how fluid pressure and speed are related when a fluid moves relative to an object such as an aerofoil.
Finally, I explained how the physics in this series of post is important in society and practical applications, such as collisions, road safety, wheels and transport in general.
Till next time, I still remain my humble self, @emperorhassy.
Thanks for reading.
REFERENCES
https://www.britannica.com/science/Bernoullis-theorem
https://en.wikipedia.org/wiki/Bernoulli%27s_principle
https://en.wikipedia.org/wiki/Airfoil
https://www.nasa.gov/sites/default/files/atoms/files/bernoulli_principle_k-4.pdf
http://www.sciencekids.co.nz/lessonplans/flight/flightintroduction.html
https://www.brainkart.com/article/Viscosity--Streamline-flow-and-Turbulent-flow_3057/
http://www.physics.usyd.edu.au/teaching/Ag/fluids/wflow1.htm
https://www.britannica.com/science/turbulent-flow
https://www.kullabs.com/classes/subjects/units/lessons/notes/note-detail/1512
https://en.wikipedia.org/wiki/Viscosity
https://www.quora.com/What-is-the-difference-between-friction-and-viscosity
https://www.britannica.com/science/Stokess-law
https://en.wikipedia.org/wiki/Stokes'_law
https://en.wikipedia.org/wiki/Automotive_aerodynamics
https://en.wikipedia.org/wiki/Automobile_drag_coefficient
https://carbiketech.com/aerodynamic-drag/
https://www.siyavula.com/read/science/grade-12/work-energy-and-power/05-work-energy-and-power-02
https://owlcation.com/stem/Force-Weight-Newtons-Velocity-and-Mass
https://en.wikipedia.org/wiki/Friction


This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.