What did Lorentz and Zeeman do to win the Nobel Prize for physics in 1902?
A few months ago I wrote a publication about how Roentgen won his Nobel Prize and explained in detail everything about his discovery "The X-Ray". As we all know, the Nobel Prize is the greatest recognition that a scientist can receive for his contribution to science. More than a century has passed since the first award was given and for decades we have been delighted with fabulous discoveries that have undoubtedly contributed to the advancement of science and above all have made people's lives easier today.

Attribution 2.0 Generic (CC BY 2.0)
That is why I have decided to return to this topic and publish this second issue where I explain the work for which these scientists were awarded this prize. If you know a little bit about me, you know that I love science, but above all physics, for this reason I am going to talk about the discovery of two Dutch scientists Hendrik Antoon Lorentz and Pieter Zeeman who in 1902 won this prize for "their research on the influence of magnetism on radiation phenomena".
But before talking about this work it is important to know what happened several years ago, where several important scientists made way for Lorentz and Zeeman to be able to do this work.
We all know that Coulomb was the precursor of electricity thanks to his laws where he determined the properties of electrostatic forces. His discovery served as a basis for other great scientists among them Michael Faraday, where thanks to his fabulous experiments in the 19th century, he discovered phenomena that today serve as the basis of electromagnetism. Faraday was a genius in the experimentation, he had a magic and unique touch that no other scientist of his time possessed, thanks to his experiments he could discover phenomena totally unknown for that time like the mutual induction or electromagnetic induction, that is not more than the effect of producing an electromotive force in a coil, due to the change of current in another coupled coil. Having said that, he created several laws that explained this phenomenon, but not everything is rosy, since Faraday only had basic knowledge about mathematics that was not very deep, and for that reason he could not create a theory that could encompass in a general way everything related to electromagnetic phenomena.

Induction experiment. CC BY-SA 3.0
Then a person was needed who was able to group all these phenomena together and create a theory that was able to describe them in a way that was simple for everyone. This is where Hans Christian Ørsted comes in, putting it all together into a theory.
But something else was still needed and it was not until the arrival of the super genius and the one that many call the father of electromagnetism as it was James Clerk Maxwell, who established the classic theory of the electromagnetic radiation, where he could demonstrate the unification of the 3 great phenomena of the physics ( electricity, magnetism and light ). Also, he created 4 beautiful equations that describe electromagnetism, where he describes the existence of perturbations of the electric and magnetic fields that were propagating through space.
Thanks to the results of the experiments by Coulomb, Gauss, Ampere, Faraday and other scientists, he was able to introduce both concepts, i.e. to unite the electric and magnetic field into one concept. Maxwell said that if an electric field oscillates in time at a certain point in space, it could be generated at that point in space and all its surroundings from a magnetic field that oscillates in time. And vice versa, he also said that if a magnetic field oscillates in time it could produce an electric field that moved in and around a point.
From the discovery and subsequent creation of their equations many unknowns arose, among which were:
If we have an electric field that varies in time and at the same time produced a magnetic field that is also variable in time, vice versa, what happened then?...
The disturbances that oscillate in space extended through it? or if on the contrary it was the vacuum, to infinity? what happened then?...
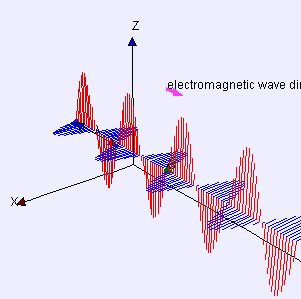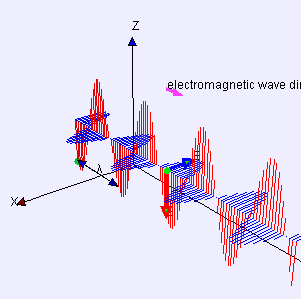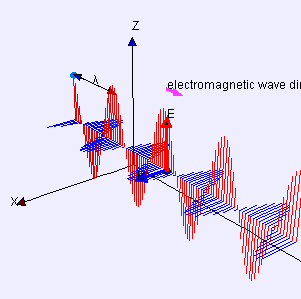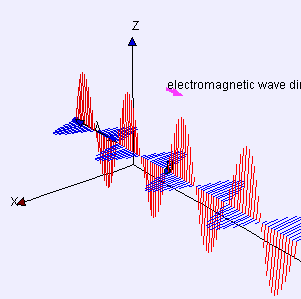
Both the electric and the magnetic field when combined produce an electromagnetic wave that propagates through space-time, but if there are electric and magnetic fields that can vary in time, then the question was where are the waves?... what are they?... is it possible to observe them?... or simply they existed a long time ago and we had not been able to detect them?...
Maxwell realized that with his equations he could answer all these questions, he noticed that in the conservation of electric charge something was missing, and that something was to introduce an additional term in the Ampere law, for that reason today this small but great detail is considered to be one of the most outstanding aspects of his work. He was also able to explain very clearly how fast electromagnetic waves travel in space-time, in fact he was able to demonstrate this since the speed at which these waves propagate in the fields could be determined perfectly by his equations due to the electrical and magnetic properties of the medium. The next part of his work was to introduce his equations into the vacuum and demonstrate the speed at which the waves were propagated and after his calculations he was able to show that it was 310,740,000 m/s, the precision of the apparatus of the time, with almost total accuracy the speed of light. By introducing the temporary derivative of an electric field, known as displacement current, and demonstrating all this, he was able to publish his work in 1865.
A Dynamical Theory of the Electromagnetic Field, modified Ampère's version of the law predicting the existence of electromagnetic waves propagating, depending on the material medium, at the speed of light in that medium. In this way Maxwell identified light as an electromagnetic wave, thus unifying optics with electromagnetism.
Heinrich Hertz later tested this theory experimentally and ushered in a new era in physics.
After this, new questions were born. And the most important was how those electric and magnetic fields that oscillate in space and produce light in bodies were generated? Although Maxwell created these fantastic equations to interpret these fields and perfectly explained the propagation of electromagnetic waves, he did not answer this question.
It was here that two fantastic Dutch scientists entered the scene, a couple who completed the theory and experimentation in a unique way that could provide an answer to this new question. They were Hendrik Antoon Lorentz and Pieter Zeeman.
Lorentz was brilliant and played a crucial role in physics in interpreting the behavior of these phenomena. Although he and the other physicists of the time were not very clear about what was going on at the time, they hypothesized that they would eventually respond to this behavior. Since matter has electrical properties and something was supposed to transmit current to conducting materials, and apart from that it also had optical properties that could emit and absorb radiation, and since they were related to what Maxwell explained in his theories. So it was quite likely that what could generate from electricity and magnetism was the same source of light radiation that materials emit and absorb.
So what does this mean?
Maxwell's equations were great but they lacked something! to clearly explain how light was produced in the body?. In these equations the variable fields produced electromagnetic waves, the matter was made up of particles that were invaluable to us with a particular charge, so could it be possible to create those waves by making those particles vibrate?. He said that particles are charged instantly when they vibrate, and therefore an electric and magnetic field was created, and in turn they could propagate in space according to his fabulous equations. So Lorentz postulated the following:
That the light was produced by the oscillation of the electrons of the atoms. Yeah, that's obvious, isn't it?..
Lorentz answered how electromagnetic waves were created in bodies, but he also clarified other questions that Maxwell's equations could not answer. One of them was that when observing the magnetized and non-magnetized bodies one could see that light did not manifest itself or did not have the same behavior in both materials, to make it a little clearer we say that the electric and magnetic fields did not present the same direction and oscillated from different directions in both the magnetized and non-magnetized bodies. But why does this happen? According to Lorentz's hypothesis a body which has magnetic properties or is magnetized has a certain degree of quantity of electrons which are orbiting in parallel planes, so that the light which these bodies emit after absorbing, because the electrons were not oscillating in random directions... Spectacular, isn't it?.
But where is Zeeman in all this? Well!! this fabulous genius performed a brilliant experiment that would serve as a major breakthrough in classical electrodynamics and take a giant step forward in quantum mechanical physics. I'll explain it in a very simple way for all of us to understand.
Thanks to the advances of that time, such as spectroscopy, and some other instruments that could identify the spectral lines. Zeeman took a Bunsen burner and produced a sodium flame, this produced an orange color which in turn produced spectral lines of approximately 590 nanometers. But this was not enough and he placed two electromagnets in the middle of the sodium flame and dramatically at that time the flames changed color, so Zeeman was immediately surprised because before we only had two colors in the flame and now with the magnets originated multiple lines of color, it was impressive for that time! By removing the magnet instantly the extra lines were completely ignored and there were only the two lines from the beginning.
However, another very important detail was that the two lines of the sodium flame had a distance of approximately 0.6 nanometers between them, but the multiple lines had a smaller distance and this was quite surprising and Zeeman himself thought he was making a mistake in his experiment.
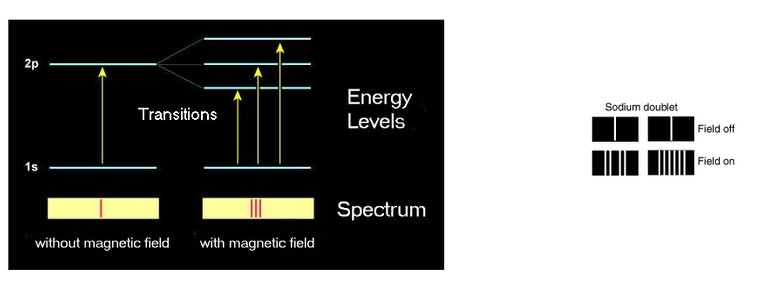
Diagram of the Zeeman experiment. Energy levels in the presence of a magnetic field and in the absence of a magnetic field BY https://www.chimicamo.org/
To check if he was not making mistakes in the experiment he decided to drill the poles of the magnets and observe inside them, and he realized that the lines of the magnetic force in their poles with respect to their direction was fine and corroborated the experiment. Similarly they reversed the phenomena, the absorption of light due to the sodium vapour, and everything was perfect. The sodium vapour equally absorbs the light of the two lines of the beginning, so if they placed the two magnets between the sodium vapour, they absorbed the light of several wavelengths and not of any wavelength. Therefore, the same phenomenon occurred if they removed the magnets, the absorption returned to normal and in conclusion the phenomenon occurred in both the flame and the vapor. Zeeman was right and it was a great find!.
Nothing more and nothing less than we would later know as the great Zeeman Effect.
Zeeman relied on Lorentz's theory and stated that everything he had proposed was quite logical, since if we had a magnetic field this would make the electrons deviate from their initial orbit and everything depended on the plane of rotation in their orbit. So if its oscillation period varied, so would the wavelength, that is, magnetism directly affects the electron causing it to behave differently without the presence of the magnetic field. In conclusion, the electrons are the source of light, and if we alter them due to the presence of the magnetic field, so does the light absorbed by the bodies.
Finally Zeeman proved that the light emitted under the action of a magnetic field would be polarized and was able to corroborate Lorentz's hypothesis using his electronic theory. Using this theory it would be possible to determine the relationship between the charge and mass of the electrons, as well as the relationship between their mass and the mass of the atoms and of course the sign of the charges. Later Thomson published his work where he explained very well the electronic behavior and its cathode rays, where it was possible to verify that the Lorentz electrons were the same as Thomsom's and that they orbited around the nucleus of the atoms.
All the experiments and works of Faraday, Maxwell and company were resolved and totally verified and physics took a very important step at that time. Other great discoveries followed which, as I mentioned earlier, opened up a new era. The era of quantum mechanics.
Friends I hope you liked my content and enjoyed this reading. Soon I will publish a little more about these great discoveries of science that opened the way to a new era.
Greetings...
Content support
Publish through our official app and you will get an extra vote of 5% https://www.steemstem.io/
 Video credits @gtg
Video credits @gtg
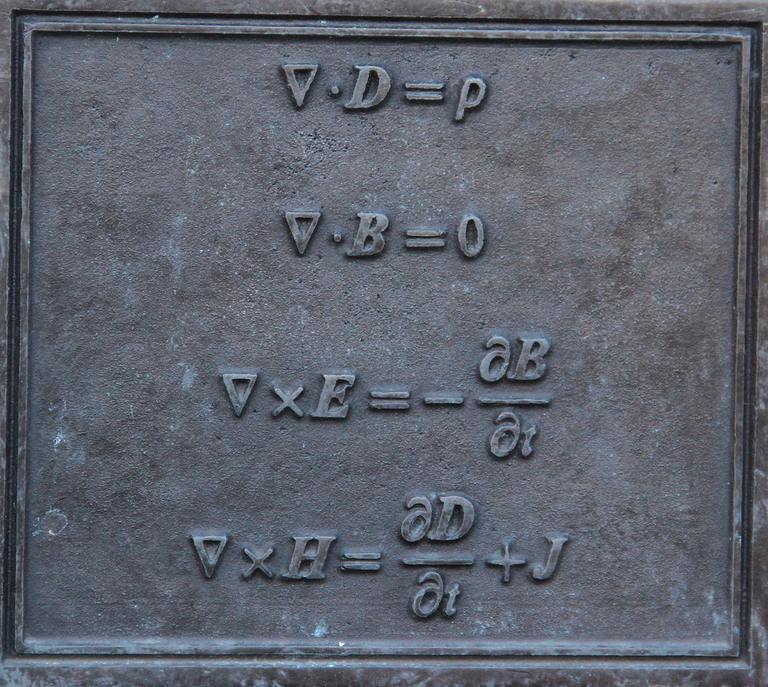


According to the Bible, Are you one of the apostles of Jesus? Why do you preach?
Watch the Video below to know the Answer...
(Sorry for sending this comment. We are not looking for our self profit, our intentions is to preach the words of God in any means possible.)
Comment what you understand of our Youtube Video to receive our full votes. We have 30,000 #SteemPower. It's our little way to Thank you, our beloved friend.
Check our Discord Chat
Join our Official Community: https://steemit.com/created/hive-182074
These names will never be forgotten in the field of Physics as their inventions and discoveries are really great contributions to science.
The first discoveries that won the Nobel Prize in physics are fantastic :)
That's right
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.
That is a great article. I enjoyed reading it. I have two side remarks (just to trigger discussions):
Cheers!
Thanks... :)
Taking the two equations /Ampere / Gauss) and generalizing them and then working with quadrivectors and contravariant tensors for me is crazy, I'm not Benjamin Fucks or Sheldon Cooper hahaha I better stick to my experimental physics hahaha
Do you think you can discover the asymmetry in the magnets? This would give a complete turn to physics and reformulate the law of Gauss and Lorentz force.. or do you not want that to happen? @lemouth
I am not "Benjamin Fucks" myself too... I have one less 'c' :D
I would be happy with anything that changes our vision of the world, TBH ^^
Sorry hehe would be fantastic to reformulate the Maxwell equations :D
Although maybe Maxwell wouldn't be too happy :P
I think that he won't care... at least anymore ;)