Prepárate para aprender cálculo infinitesimal a nivel universitario. III Parte: Ejercicios de repaso del capítulo I. Límite y sus propiedades del libro de Larson

Para esta ocasión estoy en estudio y evaluación de los límites y sus propiedades, para ello quiero que nos ubiquemos en la página 91 del libro en mención, en lo que sería los ejercicios de repaso de todo el capítulo I dedicado al estudio de los límites y sus propiedades.
En esta oportunidad quiero compartir un análisis con ustedes relacionada a la parte que dice: en los ejercicios 5 y 6, utilizar la gráfica para determinar el límite:
Ejercicio propuesto #5 (página 91 Libro de Larson. Octava edicion):
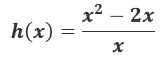
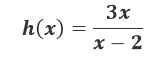
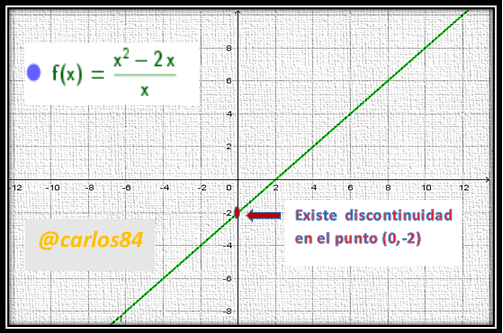
Gráfico de la función racional del ejercicio de repaso #5 del libro de Larson
Para analizar la discontinuidad en el punto (0,-2) es necesario soportarnos en resolver el límite de la función racional cuando x tiende o se aproxima a cero. Del valor que nos arroje la solución del límite es que obtenemos la coordenada en y del punto de discontinuidad, ya que la coordenada en x del punto es cero que es hacia donde se aproximan los valores de x.
Dado este planteamiento procedemos al planteamiento del límite:
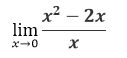

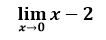
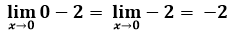
Otra interpretación bastante interesante es ver al punto (0,-2) como un punto donde la función expresa una discontinuidad, es decir que realmente si existe una imagen cuando x=0, pero solo es posible saber la imagen aplicando la teoría de límite de una función real.
Lo otro importante a destacar es que esta función racional es continua en todos los puntos del plano cartesiano excepto en el punto marcado de rojo, tal y como se puede observar en el gráfico de la función racional del ejercicio propuesto #5.
Gráfico de la función racional del ejercicio # 6 del libro de Larson.
Este gráfico fue generado mediante el uso y aplicación del software geogebra 5.0 y editado en Microsoft Word 2013.
Para el caso del ejercicio número 6 de los ejercicios de repaso del capítulo I (Límite y sus propiedades) del libro de Larson en la página 91, se nos presenta una función racional, cuyas características son que para x=2 el denominador se hace cero, lo que significa que a medida que x se aproxime a x=2 la función racional se aproxima al infinito. Como se puede ver en la gráfica x=2 representa una asíntota vertical, ahora bien surge la siguiente pregunta de análisis:
Es bajo esta circunstancia en la que la teoría de Límite de una función real viene una vez más a ayudarnos a comprender el comportamiento del gráfico de esta funcion racional, para ello nos planteamos resolver el límite de la función racional cuando x se aproxima a 2, para ello se tiene que:
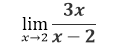
En esta ocasión si realizamos la sustitución directa del límite nos queda:
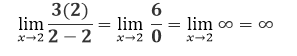
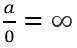
Conclusiones y análisis en base a estos dos casos de estas dos funciones racionales estudiadas de los ejercicios de repaso del libro de Larson:
[1] En la función racional del ejercicio 5 de los ejercicios de repaso de la página 91 del libro de Larson podemos expresar su gráfico en base al gráfico de una línea recta que resulta después de la factorización de la función original, quedándonos que f(x) = x-2, sin embargo hay que tener en cuenta la función racional original, ya que a la final tenemos que aplicar la teoría de límite para resolver la indeterminación 0/0 que surge de sustituir x=0, situación que solo tiene respuesta satisfactoria mediante la teoría de límite.
[2] Cuando evaluamos la continuidad de la función racional del ejercicio 5 del libro de Larson llegamos a la conclusión que representa una función discontinua, pero no el intervalo de todos los números reales, sino solamente en el punto (0,-2), lo cual se puede ver en el gráfico #1 en el punto de color rojo.
[3] Mediante la resolución del límite de la función del ejercicio 6 del libro de Larson podemos concluir que todo límite que de infinito cuando la x tiende a un número cualquiera, implica que la tendencia de ese número x=a representa una asíntota vertical de una función racional.
[4] La función racional del ejercicio 6 del libro de Larson a diferencia de la función del ejercicio 5, esta es continua en todo su recorrido, teniendo como diferencia que esta tiene una asíntota vertical en x=2.
Bueno amigos espero que les haya gustado la escogencia de estos ejercicios, en particular los ejercicios de repaso del libro de Larson octava edición (página 91), quise compartir con ustedes el abordaje y análisis de estas dos funciones racionales, en las que principalmente se analizaron y evaluaron sus gráficos, apoyándonos principalmente el software de uso libre geogebra 5.0 con alguna que otra edición hecha con las herramientas de imagen de Microsoft Word 2013.
También se analizaron y evaluaron en base a su continuidad y asíntotas presentes, por lo que les recomiendo estén atentos a nuevas publicaciones relacionadas al estudio del cálculo infinitesimal, si tienes alguna o sugerencia, por favor compártela en los comentarios, y si te gustaría que resolviera algún ejercicio del libro de Larson u otro libro de cálculo en particular no dudes en hacérmelo saber en los comentarios.
Se despide de ustedes su amigo @carlos84, hasta una próxima entrega.
Referencia consultada y recomendada:
Libro de cálculo de Larson y Hostetler. Volumen I. Octava Edición
"Para toda aquella persona que le apasiona la matemática, física, química, biología, educación e ingeniería, le recomiendo la etiqueta de #stem-español, es una comunidad que valora el contenido intelectual y académico de calidad, conservando siempre la originalidad de las publicaciones, por lo que se recomienda a todos aquellos amigos de Steemit que deseen publicar utilizando esta etiqueta a no cometer plagio".


Excelente
@tipu curate
Upvoted 👌 (Mana: 10/15 - need recharge?)
Gracias @victartex y a @tipu por el apoyo a mis publicaciones. Saludos
Estoy compartiendo el enlace de esta publicación en twitter: https://twitter.com/CARLOSJB84/status/1228159816998109184?s=20
Esta publicación ha sido votada por el proyecto Rainbow Token.
Rainbow es un token para inversores quienes reciben al menos el 90% de nuestras recompensas por curación (se distribuyen semanalmente en forma de STEEM). Acá puedes encontrar más información sobre el rainbow token.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie and @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Thanks for having used the steemstem.io app and included @steemstem in the list of beneficiaries of this post. This granted you a stronger support from SteemSTEM.
Enhorabuena, su "post" ha sido "up-voted" por @dsc-r2cornell, que es la "cuenta curating" de la Comunidad de la Discordia de @R2cornell.