Mathematical SBI contest #3 Results and Solution of the Equation
The problem of the last contest was:
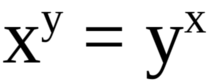
There also was an additional condition which removed the obvious solution:
x ≠ y
To find the solution you could either start guessing around, or mess around with the equation and think a little:
x^y = y^x | y = x+n
x^(x+n) = (x+n)^x
x^n = ((x+n)/x)^x
x^n = (1+n/x)^x
x^(n/x) = (1+n/x) | z = n/x
x^z = 1+z
If z would be bigger than 1, the leftern term would grow to fast compared to the linear part, since the value of x has to be 2 or bigger.
So the rightern term can be at most 2.
Also we can assume here that x is bigger than 1, because the solutions are symmetrical. If (x₁|y₁) was a solution, (-x₁|-y₁) is also a solution.
If z is smaller than 1, The leftern term would get irration(because the root of an integer cannot be rational).
So the only solution is z = 1:
x¹ = 1+1
↓
x = 2
z = 1 → y = x + 1*x = 4
The other 3 integer solution follow directly from this, so all four integer solutions are:
(2 | 4);
(4 | 2);
(-2 | -4);
(-4 | -2);
As I stated in the rules I would give those better chances who got more solutions. I will do this by giving points for each correct solution(treating the solutions where x⇌y as one solution each). So you could get a total of 2 points.
Here a table of participants(sorted by time of entry):
| Name | solutions found | score | chance of winning |
|---|---|---|---|
| @bwar | x = 4; y = 2 | 1 | 1/3 |
| @tonimontana | x = 2; y = 4 \ x = -2; y = -4 | 2 | 2/3 |
I plugged the data into a self-written random picker:
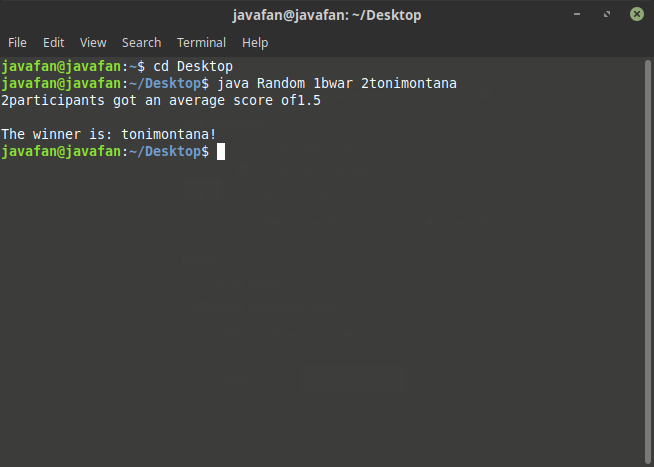
Congratulations @tonimontana. You won 1 SBI:

Hopefully I will see you in the next contest will starts tomorrow.
Oh damn, I was so close!
Come back next time, and you may win this.