Math Contest #27 Results and Solution
Solution
The problem of this contest was to proof an equivalence:
I also just noticed that this inequation only holds for uneven, positive values of n(which is probably the reason why I had no entries this week).
First of all a small explanation why this is even true:
if x is bigger than 0: Then 1/x^n is only < 1 if x > 1.
if x is smaller 0: Then 1/x^n is only < -1 if x > -1
These two cases connect both inequations.
In this case you can rearrange the leftern inequation to:
1 < x^(n+1) if x > 0 → x > 1
1 > x^(n+1) if x < 0 → 1 > ±x → -1 < ±x → -1 < x
The ± comes from taking an even root.
So if x > 0 than x > 1 is the only solution and if x < 0, x > -1 is the only solution.
Putting the 2 together gets the rightern side of the equivalence:
x > 1 or -1 < x < 0
And the way back to prove it actually is an equivalence:
x > 1 → x^(n+1) > 1 → x > 1/x^n
-1 < x < 0 → 1 < x^(n+1) → x > 1/x^n
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
List of participants with their entries:
| Name | solution found | comment |
|---|---|---|
| @tonimontana | none | found one of the errors I made → you get the reward |
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Winner draw:
Not necessary since only 1 participant:
Congratulations @tonimontana , you won 2 SBI!
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
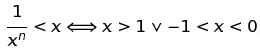
A member bonus $trendotoken tip, and !trendovoter, for @quantumdeveloper from MAPXV! These bonuses are for members, selected at random, and last for a few days.
Win MAPR tokens in this new Nonsense Writing Contest.
Also consider our MAPR fund and MAXUV vote bonds too.
MAP Steem Fintech: growing your STEEM without SP.
Congratulations @mapxv, you successfuly trended the post shared by @quantumdeveloper!
@quantumdeveloper will receive 4.97891813 TRDO & @mapxv will get 3.31927875 TRDO curation in 3 Days from Post Created Date!
"Call TRDO, Your Comment Worth Something!"
To view or trade TRDO go to steem-engine.com
Join TRDO Discord Channel or Join TRDO Web Site
Congratulations @mapxv, 47.18% upvote has been shared with your successful call on the post that shared by @quantumdeveloper!
Support @trendotoken projects by delegating : 100SP , 200SP , 500SP , 1000SP , 2000SP
Hello,
Your post has been manually curated by a @stem.curate curator.
We are dedicated to supporting great content, like yours on the STEMGeeks tribe.
Please join us on discord.
Congratulations @quantumdeveloper, your post successfully recieved 4.97891813 TRDO from below listed TRENDO callers:
To view or trade TRDO go to steem-engine.com
Join TRDO Discord Channel or Join TRDO Web Site
Congratulations @quantumdeveloper! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @quantumdeveloper! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz: