Infinite Sequences: Limits, Squeeze Theorem, Fibonacci Sequence & Golden Ratio + MORE

avatar
(Edited)

In this video, I go over an extremely extensive tutorial on Sequences as part of my new video series on Sequences and Series. Sequences are ordered lists of numbers where each term is categorized by its value and the integer corresponding to its place or order in the list. Series are summations of sequences; which I have shown in my earlier videos in finding areas and hence integrals of functions.

The topics I cover in this video include: Sequences and Notation, Definition and Precise Definition, Infinite Limits, Monotonic and Bounded Sequences, as well as the famous Fibonacci Sequence and its relationship with the also very famous Golden Ratio. And at the end of this video I go over a brief mainstream history overview of Leonardo Fibonacci. The Fibonacci sequence is the sequence in which the initial 2 terms are 1 and 1 (or 0 and 1 in modern computing) and then the terms that follow are just the summation of the previous two terms. The limit of the ratio of consecutive Fibonacci terms approach the Golden Ratio (φ) (which is the ratio of any two numbers such that it is the same as the ratio of their summation to the larger number). Fibonacci and Golden numbers/sequences/ratios/spirals/angles/etc. appear very often in all aspect of life from art, nature, design, finance, and even advertising! #AmazingStuff

Here is a list of the topics covered and their start times in the video:

  1. @ 55:54 - Introduction to Sequences and Series
  2. @ 9:25 – Sequences and Notation
  3. @ 11:06: Examples 1 to 3
  4. @ 27:30 – Limit of a Sequence
  5. @ 33:59 – Definition 1: Limit of a Sequence
  6. @ 37:38 – Definition 2: Precise Definition of a Sequence
  7. @ 47:33 – Theorem 1
  8. @ 52:26 – Definition 3: Infinite Limits of Sequences at Infinity
  9. @ 58:17 – Limit Laws for Sequences
  10. @ 1:01:39 – Squeeze Theorem for Sequences
  11. @ 1:08:10 – Theorem 2
  12. @ 1:08:51 - Examples 4 to 7
  13. @ 1:18:51 – Theorem 3
  14. @ 1:19:48 – Examples 8 to 9
  15. @ 1:26:46 – Creating Graphs of Sequences
  16. @ 1:29:33 – Example 10
  17. @ 1:41:46 – Definition 4: Monotonic Sequences
  18. @ 1:43:42 – Examples 11 and 12
  19. @ 1:54:08 – Definition 5: Bounded Sequences
  20. @ 1:59:31 – Completeness Axiom
  21. @ 2:03:43 - Monotonic Sequence Theorem
  22. @ 2:09:27 – Example 13: Recursion and Mathematical Induction
  23. @ 2:22:27 – Exercise 1: Convergence
  24. @ 2:33:20 - Exercise 2: Proof of Theorem 2
  25. @ 2:39:41 - Exercise 3: Proof of Theorem 3
  26. @ 2:48:23 - Exercise 4: Fibonacci Sequence
  27. @ 3:04:17 – Mainstream History of Fibonacci
  28. @ 3:12:04 – Overview of Fibonacci Numbers
  29. @ 3:17:33 – Overview of the Golden Ratio
  30. @ 3:21:53 – Relationship Between Fibonacci Sequence and Golden Ratio
  31. @ 3:27:06 – Golden Angle/Spiral and Approximations with Fibonacci Spiral
  32. @ 3:31:30 – Fibonacci Numbers and Golden Ratio in Nature, Art, Design, & MORE! #Amazing

Stay tuned for my next super long math video!

Watch video on:

Download video notes: https://1drv.ms/b/s!As32ynv0LoaIh68vMw9e1A75d63O3w

View Video Notes Below!

Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate

Reuse of my videos:

  • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

  • Bookmark sites/channels/accounts and check periodically
  • Remember to always archive website pages in case they get deleted/changed.

Join my private Discord chat room: https://mes.fm/chatroom

Check out my Reddit and Voat math forums:

Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow along my epic video series:

NOTE #1: If you don't have time to watch this whole video:

NOTE #2: If video volume is too low at any part of the video:

Infinite Sequences: Limits, Squeeze Theorem, Fibonacci Sequence & the Golden Ratio + MORE

Infinite Sequences.jpeg

MES Update

This is the last mathematics video I make until I finally finish my much anticipated and game-changing #AntiGravity Part 6 video. These math videos take a lot of time and brain power to complete, and which I need for finishing Part 6. I will look to remove all distractions to hopefully have the Part 6 video uploaded by the end of this year. Proving that both Classical and Quantum Mechanics are at best short-sighted, or at worst wholly wrong, will send a ripple in the Aether of Duality, so expect the video to be pretty epic!

MES Top Secret Hint: It's no coincidence that the top 3 cryptocurrencies by Market Cap are:

  1. Bitcoin
    • Bit = 1 or 0 = Duality
  2. Ether
    • The Aether
  3. Ripple XRP
    • Ripple in the Aether
    • The XRP 'X' logo is also in the shape of David LaPoint's Game-Changing Primer Fields

The Ripple in the Aether of Duality…. Remember that phrase, and maybe the order of the wording too for the near future… ;)

Anyways, enough Top Secret MES Occult Financial Advice, and now let's go over some mathematics!

Topics to Cover:

  1. Introduction to Sequences and Series
  2. Sequences and Notation
    • Example 1
    • Example 2
    • Example 3: Introduction to the famous Fibonacci Sequence
  3. Definition of the Limit of a Sequence
    • Precise Definition of the Limit of a Sequence
    • Theorem 1
    • Definition of Infinite Limits of a Sequence
    • Limit Laws for Sequences
    • Squeeze Theorem for Sequences
    • Theorem 2
    • Example 4
    • Example 5
    • Example 6: Divergence
    • Example 7: Convergence
    • Theorem 3
    • Example 8
    • Example 9: Convergence
    • Creating Graphs of Sequences
    • Example 10: Convergence
  4. Monotonic Sequences
    • Example 11
    • Example 12
  5. Bounded Sequences
    • Completeness Axiom
  6. Monotonic Sequence Theorem
    • Example 13: Recursion and Mathematical Induction
  7. End of Chapter Exercises
    • Exercise 1: Convergence
    • Exercise 2: Proof of Theorem 2
    • Exercise 3: Proof of Theorem 3
    • Exercise 4: Fibonacci Sequence
  8. Brief Mainstream History of Fibonacci
  9. Overview and Mainstream History of Fibonacci Sequence and the Golden Ratio!
    • Fibonacci Numbers
    • Golden Ratio (ϕ or φ)
    • Relationship between the Fibonacci Sequence and the Golden Ratio (φ)
      • φ is the Limit of the ratio of successive numbers of the Fibonacci Sequence!
    • Golden Angle
    • Golden Spiral
    • Golden Ratio and Fibonacci Numbers in All Aspects of Life: Nature, Art, Design, Corporations, and even Advertising! #AmazingAmazingStuff!

Introduction to Sequences and Series

Infinite sequences and series were introduced briefly in my earlier videos on "Zeno's Paradoxes" and my videos on infinite sums.

MES Note: Recall that sequences are ordered lists of numbers and series are the summation of sequences. Example: 1, 2, 3, 4 is a sequence and 1+2+3+4=10 is a series.

Their importance in calculus stems from Newton's idea of representing functions as sums of infinite series.

For instance, in finding areas he often integrated a function by first expressing it as a series and then integrating each term of the series.

We will pursue his idea in later videos in order to integrate such functions as e-x^2. (Recall that we have previously been unable to do this.)

Many of the functions that arise in mathematical physics and chemistry such as Bessel functions, are defined as sums of series, so it is important to be familiar with the basic concepts of convergence of infinite sequences and series.

Physicists also use series in another way, as we'll see in later videos.

In studying fields as diverse as optics, special relativity, and electromagnetism, they analyze phenomena by replacing a function with the first few terms in the series that represents it.

Here is a Small Preview of some of the types of series and functions that will be covered in later videos.

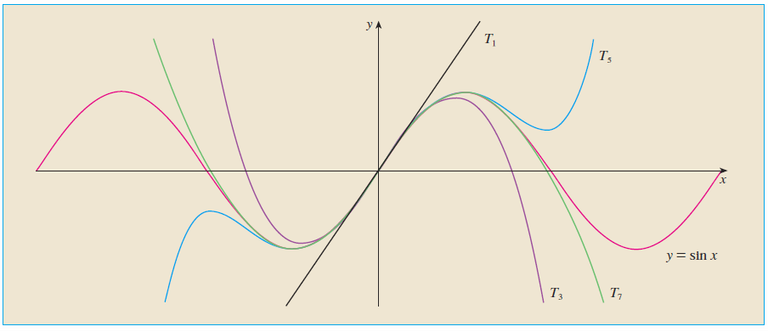
The partial sums Tn of a Taylor series provide better and better approximations to a function as n increases.

Bessel functions, which are used to model the vibrations of drumheads and cymbals, are defined as sums of infinite series.

Notice how closely the computer generated models (which involve Bessel functions and cosine functions) match the photograph of a vibrating rubber membrane.

Sequences

A sequence can be thought of as a list of numbers written in a definite order:

a1 , a2 , a3 , a4 , … , an , …

The number a1 is called the first term, a2 is the second term, and in general an is the nth term.

We will deal exclusively with infinite sequences and so each term an will have a successor a an+1.

Notice that for every positive integer n there is a corresponding number an and so a sequence can be defined as a function whose domain is the set of positive integers.

But we usually write an instead of the function notation f(n) for the value of the function at the number n.

Notation

The sequence {a1 , a2 , a3 , … } is also denoted by

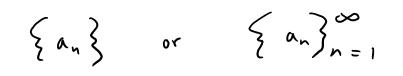
Example 1

Some sequences can be defined by giving a formula for the nth term.

In the following examples we give three descriptions of the sequence:

  1. One by using the preceding notation
  2. Another by using the defining formula
  3. And a third by writing out the terms of the sequence.

Notice that n doesn't have to start at 1.

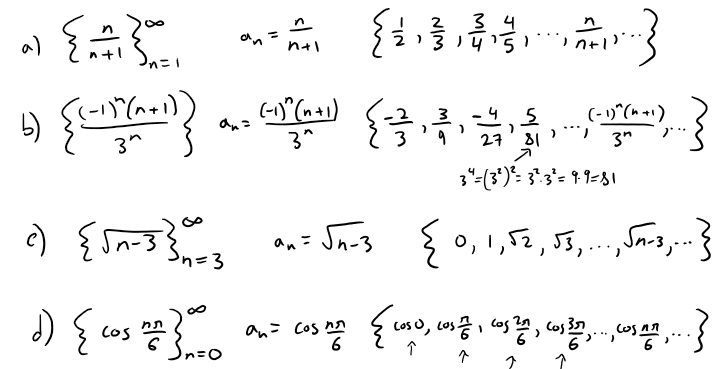
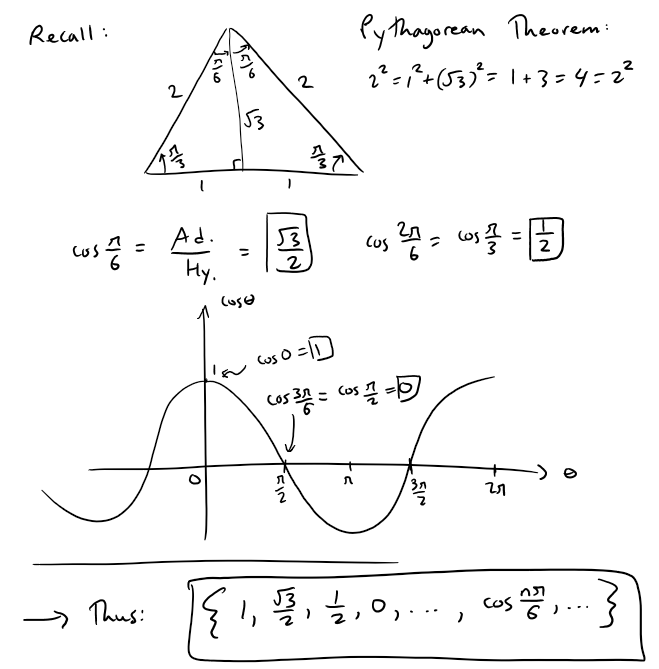
Example 2

Find a formula for the general term an of the sequence

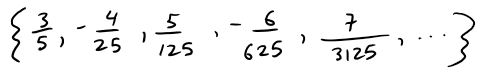
assuming that the pattern of the first few terms continues.

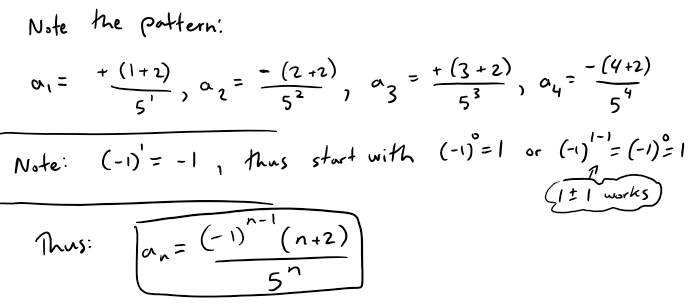
Example 3:

Here are some sequences that don't have a simple defining equation.

a) The sequence {pn}, where pn is the population of the world as of January 1 in the year n.

b) If we let an be the digit in the nth decimal place of the number e (2.7182818…), then {an} is a well-defined sequence whose first few terms are:

{7, 1, 8, 2, 8, 1, 8, 2, 8, 4, 5, … }

c) The Fibonacci sequence {fn} is defined recursively by the conditions

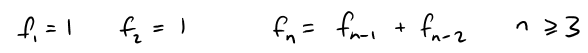
Each term is the sum of the two preceding terms.

The first few terms are:

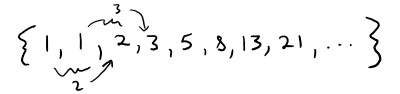
This sequence arose when the 13th-century Italian mathematician known as Fibonacci solved a problem concerning the breeding of rabbits.

I go over this problem in Exercise 4 at the end of this video as well as cover briefly on Fibonacci's life so stay tuned!

Limit of a Sequence

A sequence such as the one in Example 1a), an = n/(n + 1), can be pictured either by plotting its terms on a number line or by plotting its graph as in the figures below.

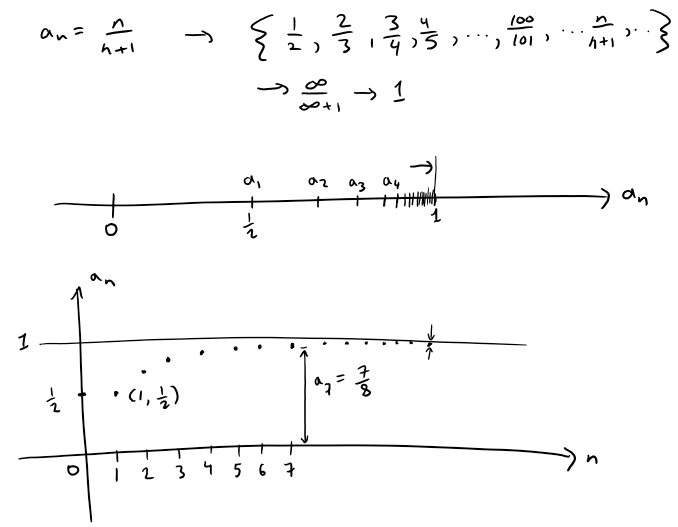
Note that, since a sequence is a function whose domain is the set of positive integers, its graph consists of isolated points with the following coordinates:

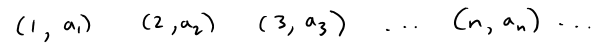
From the above figures it appears that the terms of the sequence an = n/(n + 1) are approaching 1 as n becomes large.

In fact, the difference

can be made as small as we like by taking n sufficiently large.

We indicate this by writing:

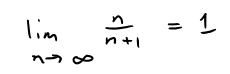
In general, the notation

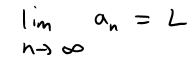
means that the terms of the sequence {an} approach L as n becomes large.

Notice that the following definition of the limit of a sequence is very similar to the definition of a limit of a function at infinity given in my earlier videos.

Recall the Definition for Limits at Infinity from my Early Videos:

This is very similar to the following definition for the limit of a sequence.

Definition 1

A sequence {an} has the limit L and we write

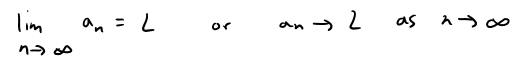
if we can make the terms an as close to L as we like by taking n sufficiently large.

If lim n→∞ an exists, we say the sequences converges (or is convergent).

Otherwise, we say the sequence diverges (or is divergent).

The graphs below shows two sequences that have a limit L.

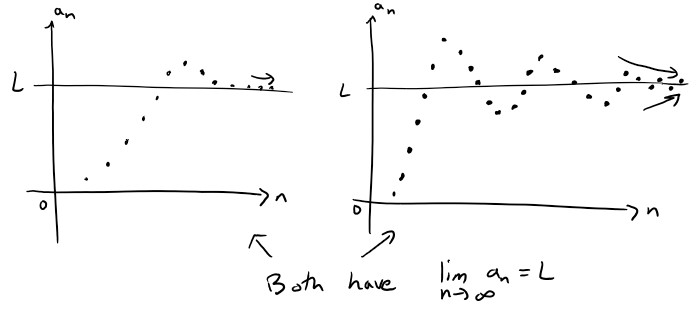
A more precise version of the above definition is as follows

Definition 2

A sequence {an} has the limit L and we write

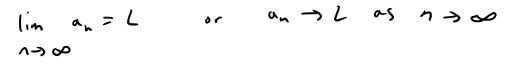
If for every ε > 0 there is a corresponding integer N such that

The precise definition of a sequence is illustrated by the figure below, in which the terms a1 , a2 , a3 , … are plotted on a number line.

No matter how small an interval (L - ε , L + ε) is chosen, there exists an N such that all terms of the sequence from aN+1 onward must lie in that interval.

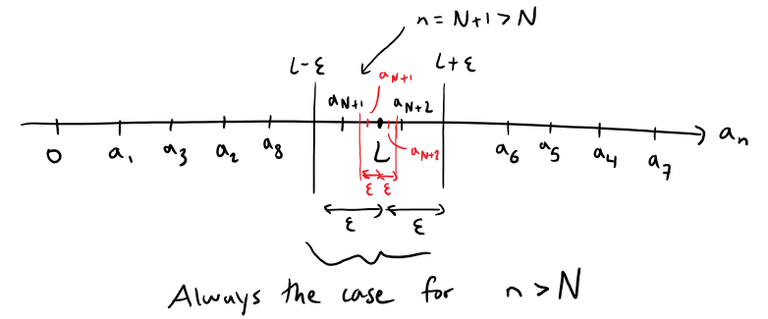
Note that the above figure shows that ANY number ε greater than 0 will always have a corresponding number N less than n.

Another illustration of this precise definition is given in the figure below.

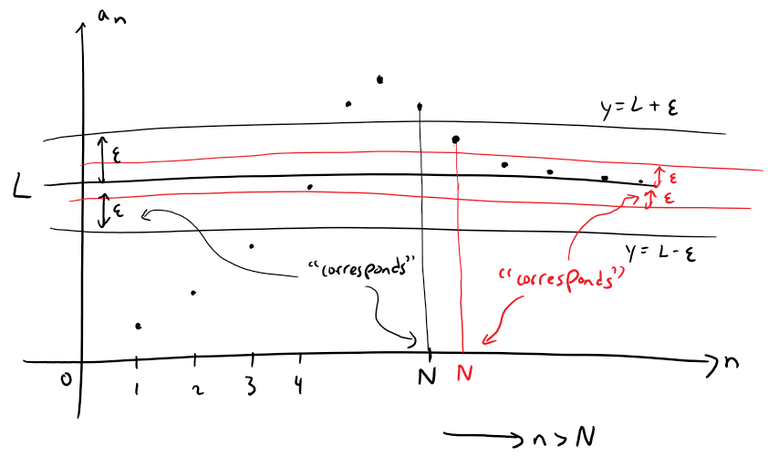
Thus shrinking the above intervals, i.e. making ε smaller, just moves the corresponding N further to the right towards n.

The points on the graph of {an} must lie between the horizontal lines y = L + ε and y = L - ε if n > N.

This picture must be valid no matter how small ε is chosen, but usually a smaller ε requires a larger N.

If you compare the precise definition with that in my earlier video on the precise definition of limits at infinity, you will see that the only difference between the two is that n is required to be an integer.

Thus we have the following theorem, and which is illustrated below.

Theorem 1

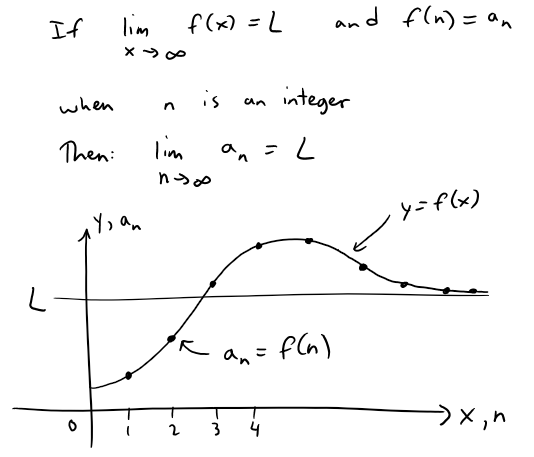
In particular let's take a look at the following limit.

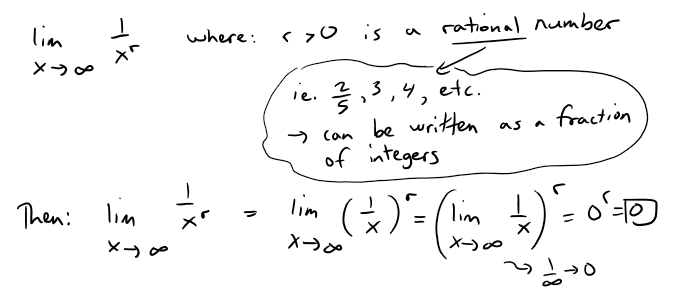
Writing this in sequence form, we get:

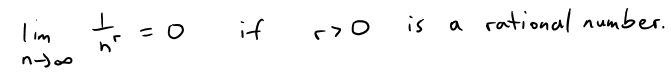
Infinite Limits of Sequences at Infinity

If an becomes large as n becomes large, we use the notation:

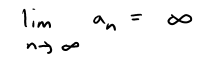
The following precise definition is similar to my earlier video's definition for infinite limits at infinity.

Definition 3

The Limit:

means that for every positive number M there is an integer N such that:

Thus for any number M regardless of how large it is, the sequence has a point that is larger (i.e. always increasing).

Compare with my earlier video's definition for infinite limits at infinity.

Graphically both these definitions are illustrated below:

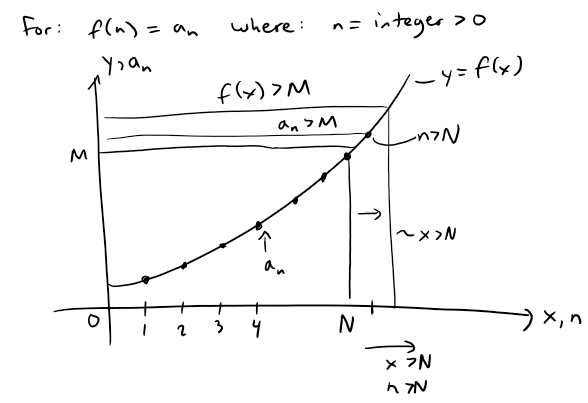
Thus again, this graph needs to be valid no matter how large N is chosen.

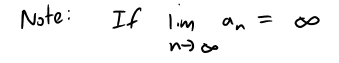
Then {an} is divergent but in a special way and we say that {an} diverges to infinity or ∞.

Limit Laws for Sequences

The Limit Laws given in my earlier videos also hold for the limits of sequences and their proofs are similar (i.e. we essentially just replace the functions with sequences as per Theorem 1).

If {an} and {bn} are convergent sequences and c is a constant,

The Squeeze Theorem can also be adapted for sequences as follows.

First recall the general Squeeze Theorem.

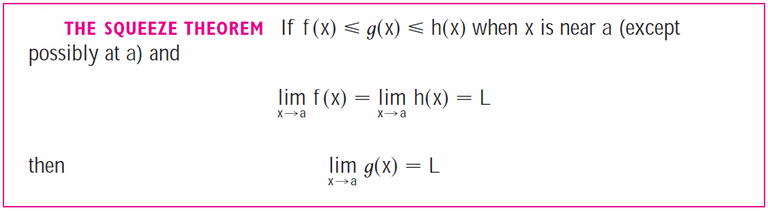
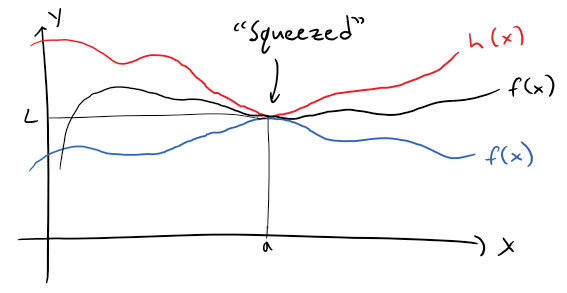
Thus for sequences we can write the Squeeze Theorem as follows:

Squeeze Theorem for Sequences

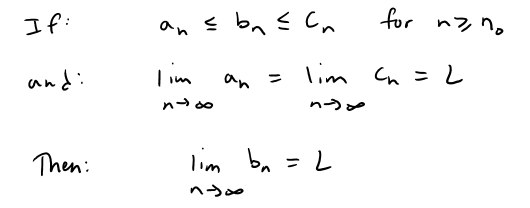
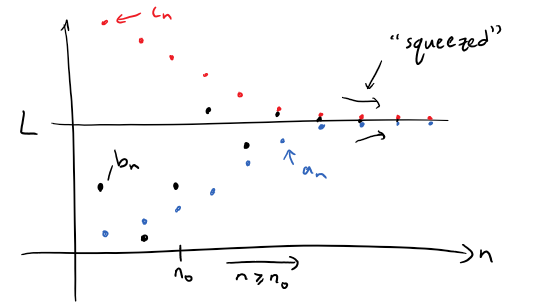
Graphically we can see this as follows:

Another useful fact about limits of sequences is given by the following theorem, which I prove at the end of this video in Exercise 2:

Theorem 2

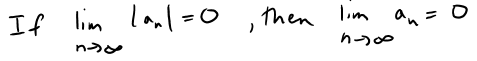
Example 4

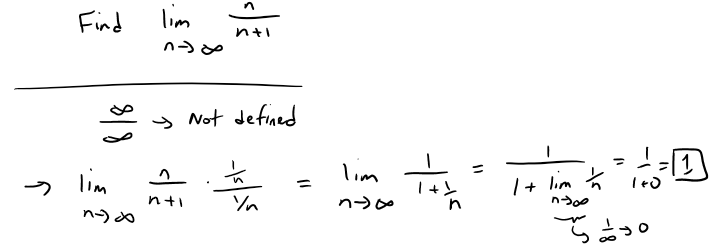
Note this is the same limit we looked at earlier in this video but this time evaluated directly to prove that it is indeed equal to 1.

Example 5

Note: We can't apply l'Hospital's Rule directly since it applies to functions of a real variable and not to sequences, but we can do a work around and then apply Theorem 1 relating the limits of functions to sequences.

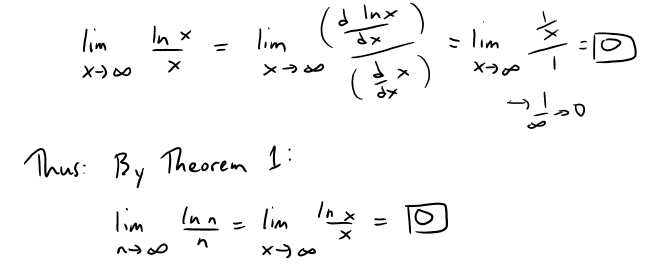
Example 6

Determine whether the sequence an = (-1) n is convergent or divergent.

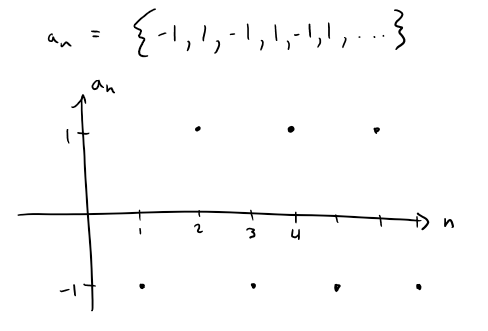
Since the terms oscillate between 1 and -1 infinitely often, an does not approach any number.

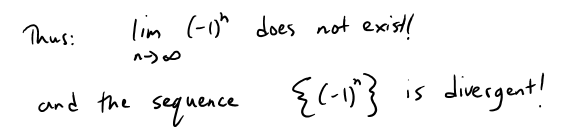
Example 7

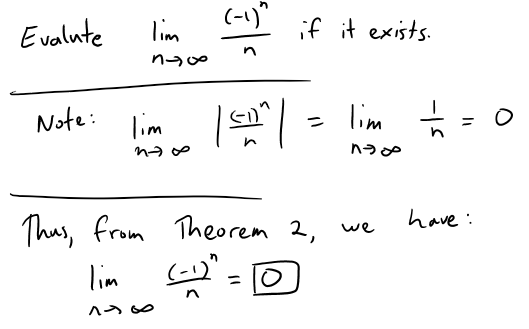
This can be seen graphically.

The following theorem says that if we apply a continuous function to the terms of a convergent sequence, the result is also convergent.

Theorem 3

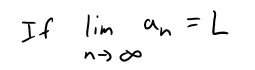
and the function f is continuous at L, then:

I prove this Theorem later in this video in Exercise 3, so stay tuned!

Example 8

And since the sine function is continuous at 0, Theorem 3 enables us to write:

Example 9

Discuss the convergence of the sequence:

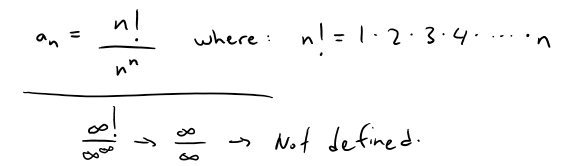
Note also that we can't use l'Hospital's Rule because the corresponding function x! is not defined when x is not an integer.

Let's write out a few terms to get a feeling for what happens to an as n gets large:

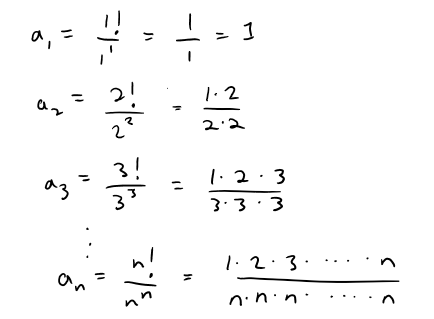
It appears from these expressions that the terms are decreasing, and perhaps approach 0.

To confirm this, observe that for the nth term we can rewrite the expression as follows:

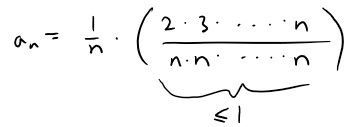
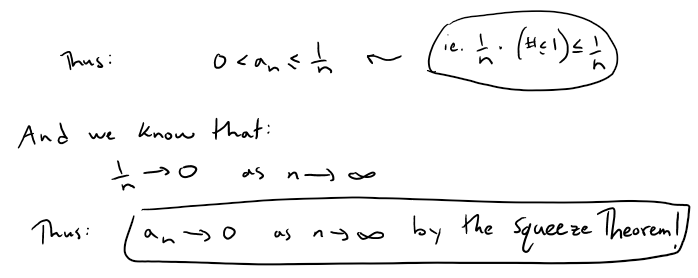
Notice that the expression in parentheses is at most 1 because the numerator is less than (or equal to) the denominator.

Creating Graphs of Sequences

Some computer algebra systems have special commands that enable us to create sequences and graph them directly.

With most graphing calculators, however, sequences can be graphed by using parametric equations.

For instance, the sequence in Example 9 can be graphed by entering the parametric equations

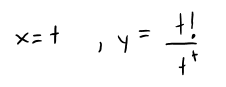
and graphing in dot mode, starting with t = 1 and setting the t-step equal to 1.

I'm not sure which calculator my calculus book was referring to, but the trusty Desmos Calculator always has a way to graph just about any function!

https://www.desmos.com/calculator/tbfrsprr03

Retrieved: 6 November 2018
Archive: Not Available

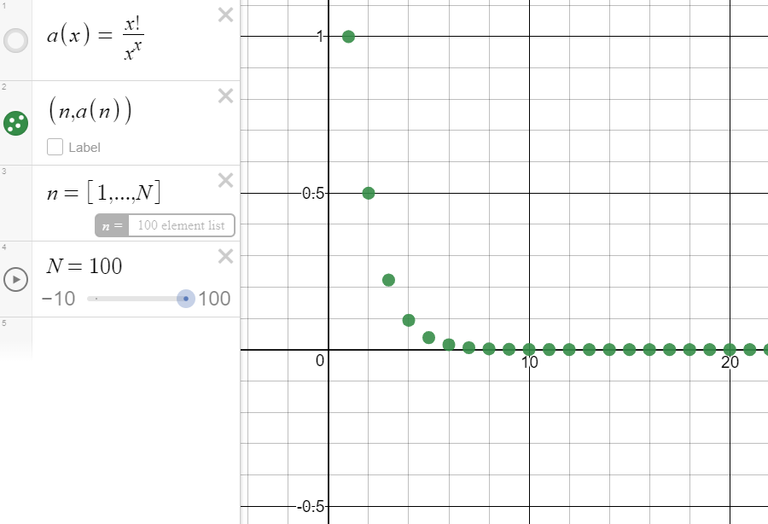
The graph converges very quickly to 0 after about the 10th term. #Nice

Example 10:

For what values of r is the sequence {rn} convergent?

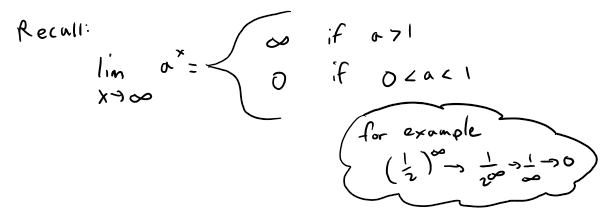
Thus, we can replace a with r, and x with n, as with Theorem 1, to get:

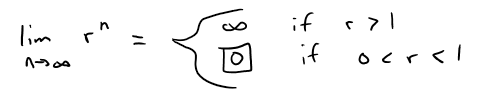
Let's now consider the trivial cases of r = 1 and r = 0.

The following graphs plot various values of r.

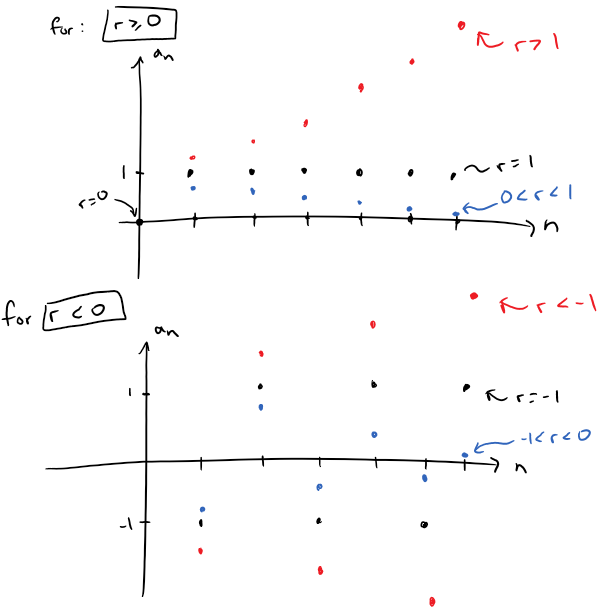
The results of Example 10 are summarized below:

The sequence {rn} is convergent if -1 < r ≤ 1 and divergent for all other values of r.

Monotonic Sequences

Definition 4

A is sequence {an} is called increasing, if:

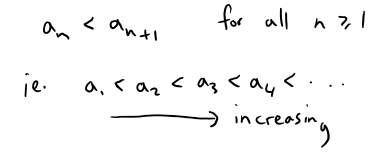
It is called decreasing if:

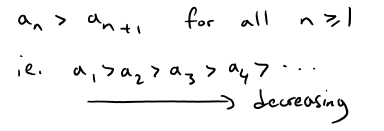
It is called Monotonic if it is either increasing or decreasing.

Example 11

Evaluate whether the following sequence is increasing or decreasing.

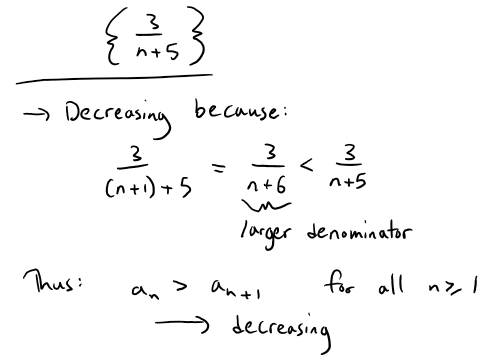
Example 12

Show that the following sequence is decreasing.

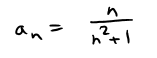
**Solution 1: We must show that an+1 < an , that is:

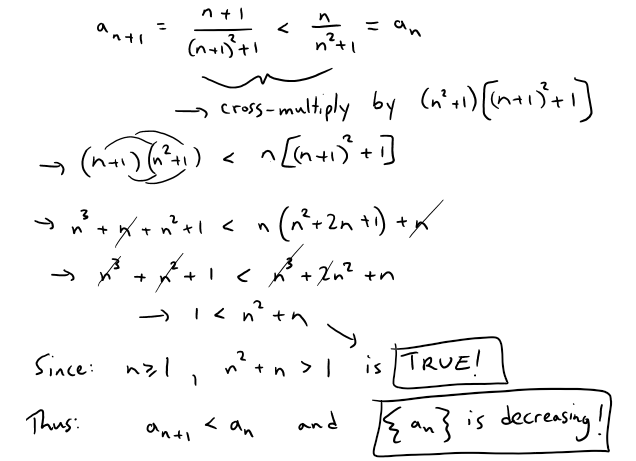
Solution 2: Consider the following function:

Now Let's Now Go Over "Bounded" Sequences

Definition 5

A sequence {an} is bounded above if there is a number M such that:

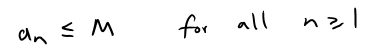
It is bounded below if there is a number m such that:

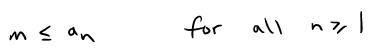
If it is bounded above and below, then {an} is a bounded sequence.

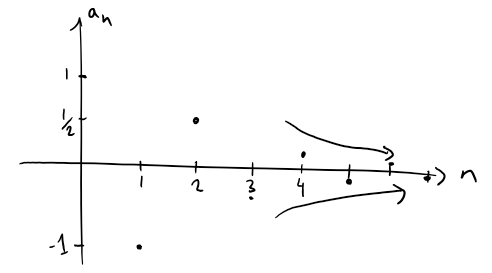
For instance, the sequence an = n is bounded below (an > 0) but not above.

The sequence an = n/(n+1) is bounded below and above since 0 < an < 1 for all n.

We know that not every bounded sequence is convergent; and an instance is shown below:

We also know that not every monotonic (i.e. increasing or decreasing) sequence is convergent (an = n → ∞).

But if a sequence is both bounded and monotonic, then it must be convergent.

This fact is proved as the following Theorem, but intuitively you can understand why it is true by looking at the figure below.

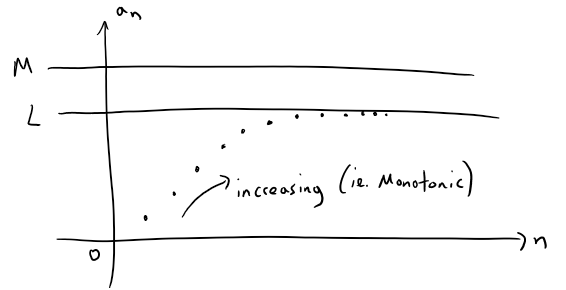
If {an} is increasing and an ≤ M for all n, then the terms are forced to crowd together and approach some number L, which could even be equal to M.

The proof of the following theorem is based on the Completeness Axiom for the set R of real numbers, which says that if S is a nonempty set of real numbers that has an upper bound M (x ≤ M for all x in S), then S has a least upper bound b. (This means that b is an upper bound for S, but if M is any other upper bound, then b ≤ M.)

The Completeness Axiom is an expression of the fact that there is no gap or hole in the real number line.

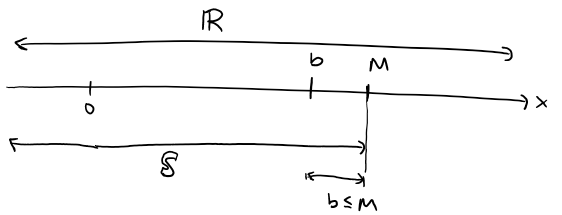
Essentially "no gap or hole" means that every number can have infinitely amount of numbers past the decimal place; hence a "least upper bound" b can ALWAYS be found that is b ≤ M.

https://en.wikipedia.org/wiki/Completeness_of_the_real_numbers

Retrieved: 8 November 2018
Archive: http://archive.fo/JgxrT

Completeness of the real number

Intuitively, completeness implies that there are not any “gaps” (in Dedekind's terminology) or “missing points” in the real number line. This contrasts with the rational numbers, whose corresponding number line has a “gap” at each irrational value. In the decimal number system, completeness is equivalent to the statement that any infinite string of decimal digits is actually a decimal representation for some real number.

Depending on the construction of the real numbers used, completeness may take the form of an axiom (the completeness axiom), or may be a theorem proven from the construction. There are many equivalent forms of completeness, the most prominent being Dedekind completeness and Cauchy completeness (completeness as a metric space).

Very interesting!

Monotonic Sequence Theorem

Every bounded, monotonic sequence is convergent.

Proof:

Suppose {an} is an increasing (hence monotonic) and bounded sequence.

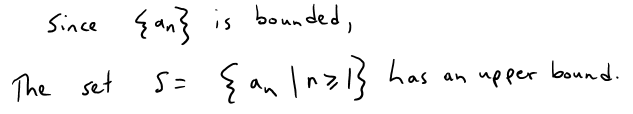
By the Completeness Axiom, it has a least upper bound L.

Given ε > 0, L - ε is not an upper bound for S (since L is the least upper bound and L - ε is less than the least upper bound).

Therefore:

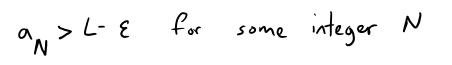
But the sequence is increasing so an ≥ aN for every n > N.

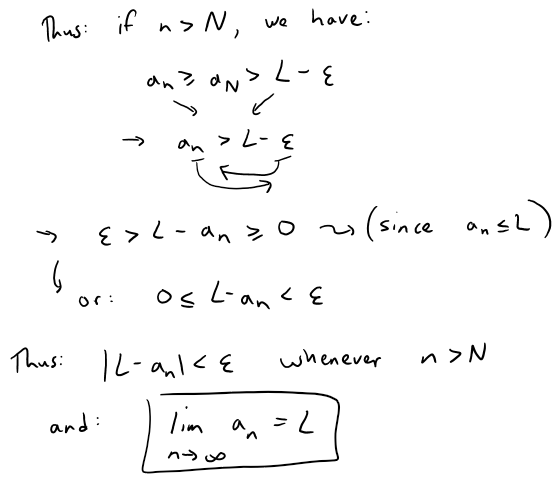
A similar proof (using the greatest lower bound) works if {an} is decreasing.

The proof of the above theorem shows that a sequence that is increasing and bounded above is convergent.

Likewise, a decreasing sequence that is bounded below is convergent.

This fact is used many times in dealing with infinite series.

Example 13

Investigate the sequence {an} defined by the recurrence relation

Solution:

We begin by computing the first several terms:

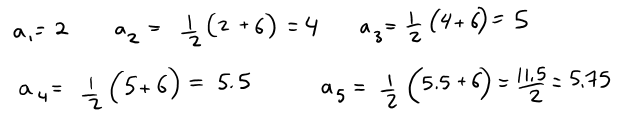
a5 = 11.5/2 = 5.75
a6 = (5.75 + 6) / 2 = 5.875
a7 = (5.875 + 6) / 2 = 5.9375
a8 = (5.9375 + 6) / 2 = 5.96875
a9 = (5.96875 + 6) / 2 = 5.984375

These initial terms suggest that the sequence is increasing and the terms are approaching 6.

To confirm that the sequence is increasing, we can use mathematical induction.

Note: Mathematical induction is often used in dealing with recursive sequences.

Recall from my earlier videos the principle of Mathematical Induction.

Let's Apply Mathematical Induction to show that an+1 > an for n ≥ 1.

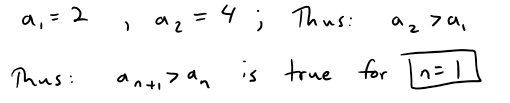
If we assume that an+1 > an is true for all n = k, then we have:

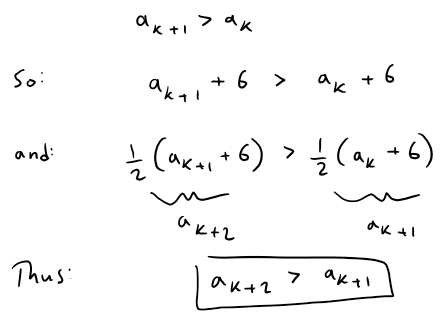
We have deduced that an+1 > an is true for n = k + 1.

Therefore the inequality is true for all n by induction.

Next we verify that {an} is bounded by showing that an < 6 for all n.

Since the sequence is increasing, we already know that it has a lower bound: an ≥ a1 = 2 for all n.

We know that a1 < 6, so the assertion is true for n = 1.

Suppose it is true for n = k; then:

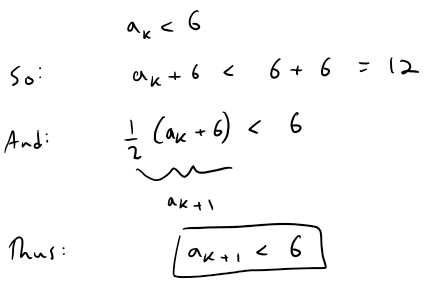
This shows, by mathematical induction, that an < 6 for all n.

Since the sequence {an} is increasing (monotonic) and bounded, the Monotonic Sequence Theorem guarantees that it has a limit.

The theorem doesn't tell us what the value of the limit is.

But now that we know the limit exists, we can use the recurrence relation to write:

Note: A proof of this fact is shown in Exercise 1 at the end of this video!

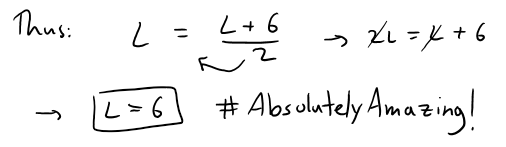
This is the End of this section in my Calculus Book, but now I will Solve some of the Proofs and Exercises that were alluded too.

The following Exercise proves the statement used in Example 13.

Exercise 1:

(a) If {an} is convergent, show that

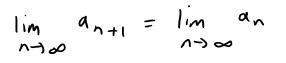
(b) A sequence {an} is defined by

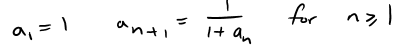
Assuming that {an} is convergent, find its limit.

Solution:

Recall Definition 2 from earlier in this video, the precise definition of a sequence (which I have just copied and pasted from my calculus book for convenience).

Now if we replace n with n + 1 in the above definition we get:

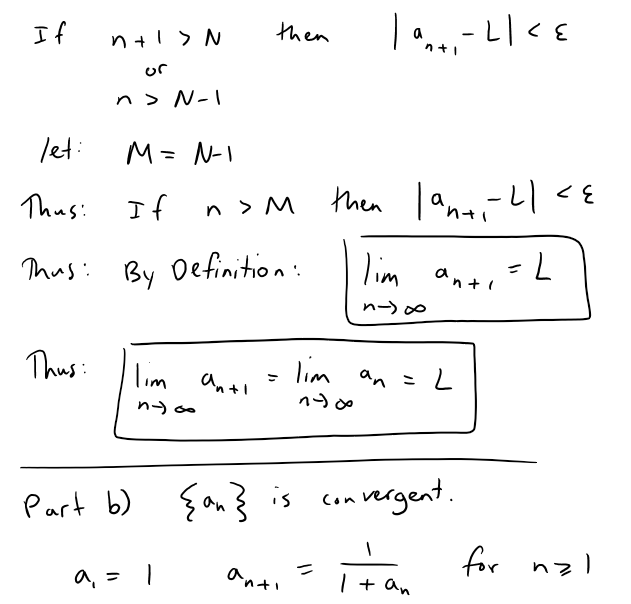
Note: L = (-1 + sqrt(5))/2 = 0.618033988749895

Exercise 2:

Prove Theorem 2 mentioned earlier in this video.

[Hint: Use either Definition 2 or the Squeeze Theorem.]

Solution 1: Squeeze Theorem

Recall Theorem 2.

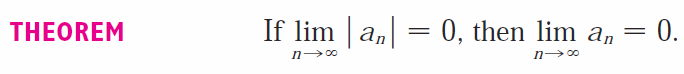
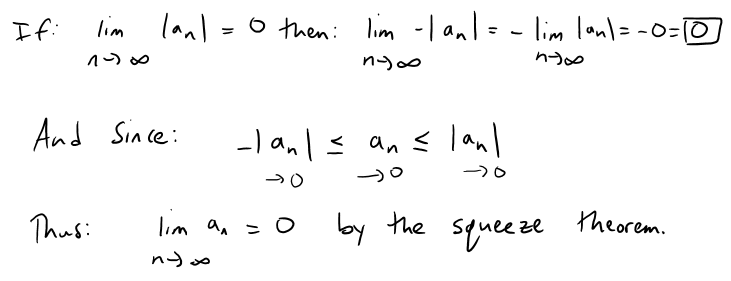
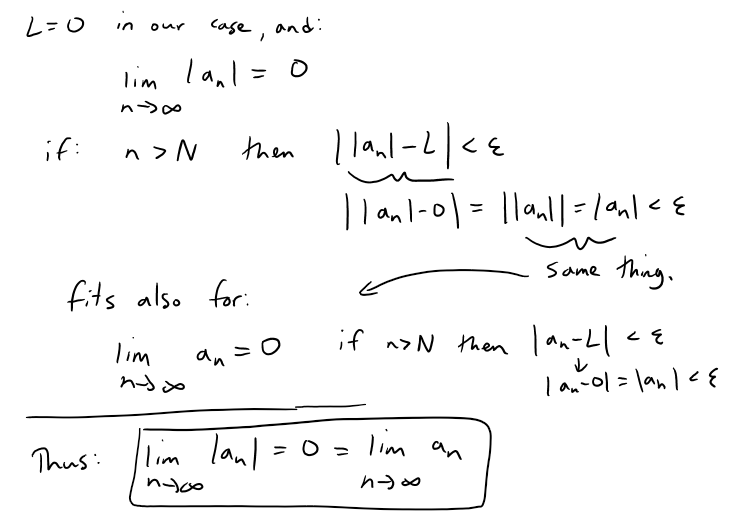
Solution 2: Using Definition 2 (Precise Definition for Sequences)

Exercise 3:

Prove Theorem 3 also mentioned earlier.

Solution:

Recall Theorem 3:

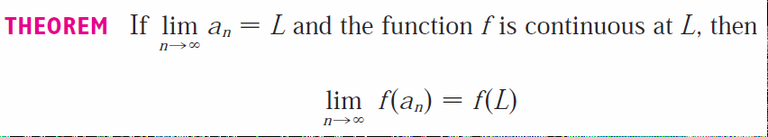
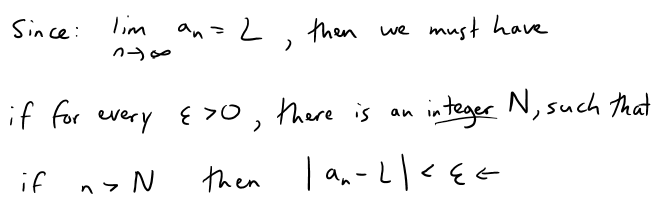
And since f is continuous at L, by the precise definition of limits shown in my earlier videos, we must have:

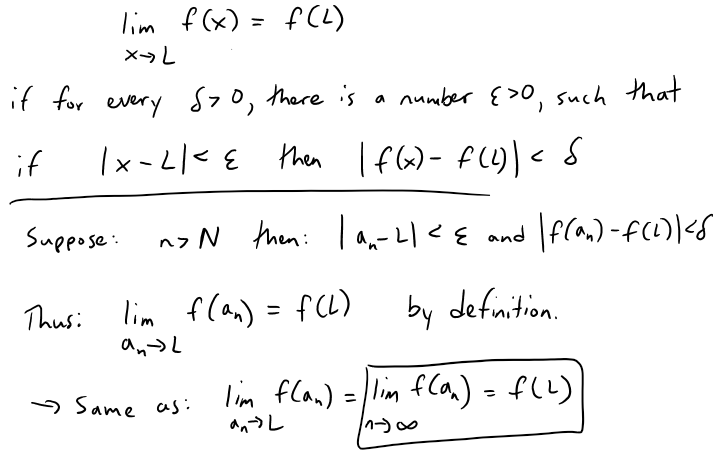
Exercise 4:

(a) Fibonacci posed the following problem:

Suppose that rabbits live forever and that every month each pair produces a new pair which becomes productive at age 2 months.

If we start with one newborn pair, how many pairs of rabbits will we have in the nth month?

Show that the answer is fn, where {fn} is the Fibonacci sequence defined in Example 3c.

(b) Let an = fn+1 / fn and show that an-1 = 1 + 1/an-2.

Assuming that {an} is convergent, find its limit.

Solution:

(a) Recall the Fibonacci sequence defined in Example 3c.

Let an be the number of rabbit pairs in the nth month.

In the nth month, each pair that is 2 or more months old (that is an-2 pairs) will produce a new pair to add to the an-1 pairs already present.

In other words, all the rabbits that are present from 2+ months ago multiply so we add the total number of rabbits from that time period to the total number of rabbits from 1 month ago since this number has newborn rabbits that haven't matured yet.

L = (1 + sqrt(5)) / 2 = 1.618033988749895

Note: This limit is in fact the Golden Ratio which I will discuss further below in this video so stay tuned!

Finally, Let's Go over a Brief Mainstream History of Fibonacci

https://en.wikipedia.org/wiki/Fibonacci

Retrieved: 12 November 2018
Archive: http://archive.fo/s6m2t

Fibonacci

Fibonacci (c. 1175 – c. 1250)[2] was an Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages".[3] The name he is commonly called, "Fibonacci" (Italian: [fiboˈnattʃi][4]), was made up in 1838 by the Franco-Italian historian Guillaume Libri[5] and is short for filius Bonacci ("son of (the) Bonacci")[6] and he is also known as Leonardo Bonacci, Leonardo of Pisa, Leonardo Pisano Bigollo, or Leonardo Fibonacci.

Fibonacci popularized the Hindu–Arabic numeral system in the Western World[7]primarily through his composition in 1202 of Liber Abaci (Book of Calculation).[8] He also introduced Europe to the sequence of Fibonacci numbers, which he used as an example in Liber Abaci.[9]

Statue of Fibonacci (1863) by Giovanni Paganucci in the Camposanto di Pisa

History

Fibonacci was born around 1175 to Guglielmo, a wealthy Italian merchant and, by some accounts, the consul for Pisa. Guglielmo directed a trading post in Bugia, a port in the Almohad dynasty's sultanate in North Africa. Fibonacci travelled with him as a young boy, and it was in Bugia (now Béjaïa, Algeria) that he learned about the Hindu–Arabic numeral system.[2]

Fibonacci travelled extensively around the Mediterranean coast, meeting with many merchants and learning about their systems of doing arithmetic. He soon realised the many advantages of the Hindu-Arabic system. In 1202, he completed the Liber Abaci (Book of Abacus or Book of Calculation) which popularized Hindu–Arabic numerals in Europe.[2]

Fibonacci became a guest of Emperor Frederick II, who enjoyed mathematics and science. In 1240, the Republic of Pisa honored Fibonacci (referred to as Leonardo Bigollo)[10] by granting him a salary in a decree that recognized him for the services that he had given to the city as an advisor on matters of accounting and instruction to citizens.[11]

The date of Fibonacci's death is not known, but it has been estimated to be between 1240[12] and 1250,[13] most likely in Pisa.

Liber Abaci (1202)
Main article: Liber Abaci

In the Liber Abaci (1202), Fibonacci introduced the so-called modus Indorum (method of the Indians), today known as the Hindu–Arabic numeral system.[14][15] The book advocated numeration with the digits 0–9 and place value. The book showed the practical use and value of the new Hindu-Arabic numeral system by applying the numerals to commercial bookkeeping, converting weights and measures, calculation of interest, money-changing, and other applications. The book was well-received throughout educated Europe and had a profound impact on European thought. No copies of the 1202 edition are known to exist.[16]

The 1228 edition, first section introduces the Hindu-Arabic numeral system and compares the system with other systems, such as Roman numerals, and methods to convert the other numeral systems into Hindu-Arabic numerals. Replacing the Roman numeral system, its ancient Egyptian multiplication method, and using an abacus for calculations, with a Hindu-Arabic numeral system was an advance in making business calculations easier and faster, which led to the growth of banking and accounting in Europe.[17][18]

The second section explains the uses of Hindu-Arabic numerals in business, for example converting different currencies, and calculating profit and interest, which were important to the growing banking industry. The book also discusses irrational numbers and prime numbers.[16][17][18]

A page of Fibonacci's Liber Abaci from the Biblioteca Nazionale di Firenze showing (in box on right) the Fibonacci sequence with the position in the sequence labeled in Roman numerals and the value in Hindu-Arabic numerals.

Fibonacci sequence
Main article: Fibonacci number

Liber Abaci posed, and solved, a problem involving the growth of a population of rabbits based on idealized assumptions. The solution, generation by generation, was a sequence of numbers later known as Fibonacci numbers. Although Fibonacci's Liber Abaci contains the earliest known description of the sequence outside of India, the sequence had been noted by Indian mathematicians as early as the sixth century.[19][20][21][22]

In the Fibonacci sequence of numbers, each number is the sum of the previous two numbers. Fibonacci began the sequence not with 0, 1, 1, 2, as modern mathematicians do but with 1, 1, 2, etc. He carried the calculation up to the thirteenth place (fourteenth in modern counting), that is 233, though another manuscript carries it to the next place: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377.[23][24] Fibonacci did not speak about the golden ratio as the limit of the ratio of consecutive numbers in this sequence.

Legacy

In the 19th century, a statue of Fibonacci was constructed and raised in Pisa. Today it is located in the western gallery of the Camposanto, historical cemetery on the Piazza dei Miracoli.[25]

Interesting Stuff!

https://www.express.co.uk/life-style/top10facts/621378/10-things-FIBONACCI

Retrieved: 15 November 2018
Archive: Not Available

Now Let's Quickly go over some of the Mainstream History and Overview of the Fibonacci Sequence and its Close Relationship with the Golden Ratio! #FascinatingStuff!

https://en.wikipedia.org/wiki/Fibonacci_number

Retrieved: 12 November 2018
Archive: http://archive.fo/f0br5

Fibonacci Number

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number after the first two is the sum of the two preceding ones:[1][2]

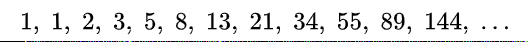
Often, especially in modern usage, the sequence is extended by one more initial term:

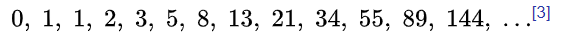
By definition, the first two numbers in the Fibonacci sequence are either 1 and 1, or 0 and 1, depending on the chosen starting point of the sequence, and each subsequent number is the sum of the previous two.

The sequence Fn of Fibonacci numbers is defined by the recurrence relation:

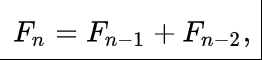
with seed values[1][2]

or[5]

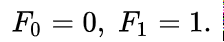
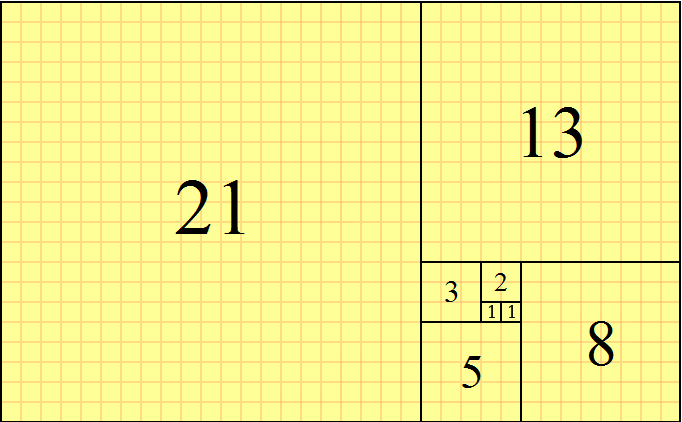
A tiling with squares whose side lengths are successive Fibonacci numbers

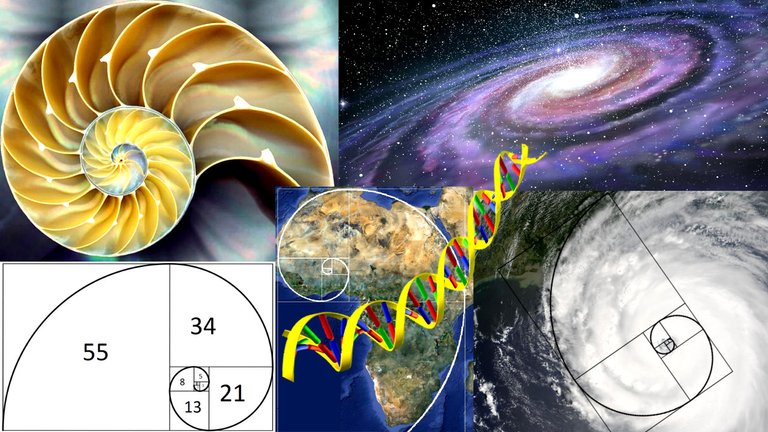
MES Note: VERY interesting how the side lengths match up with the previous squares as they spiral around!

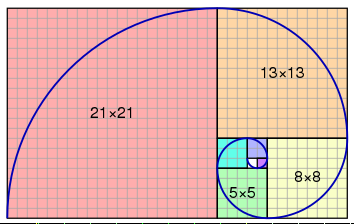
The Fibonacci spiral: an approximation of the golden spiral created by drawing circular arcs connecting the opposite corners of squares in the Fibonacci tiling;[4] this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13 and 21.

Fibonacci numbers appear to have first arisen in perhaps 200 BC in work by Pingala on enumerating possible patterns of poetry formed from syllables of two lengths. The Fibonacci sequence is named after Italian mathematician Leonardo of Pisa, known as Fibonacci. His 1202 book Liber Abaci introduced the sequence to Western European mathematics,[6] although the sequence had been described earlier in Indian mathematics.[7][8][9] The sequence described in Liber Abaci began with F1 = 1. Fibonacci numbers were later independently discussed by Johannes Kepler in 1611 in connection with approximations to the pentagon. Their recurrence relation appears to have been understood from the early 1600s, but it has only been in the past very few decades that they have in general become widely discussed.[10]

…

They are intimately connected with the golden ratio; for example, the closest rational approximations to the ratio are 2/1, 3/2, 5/3, 8/5, ... .

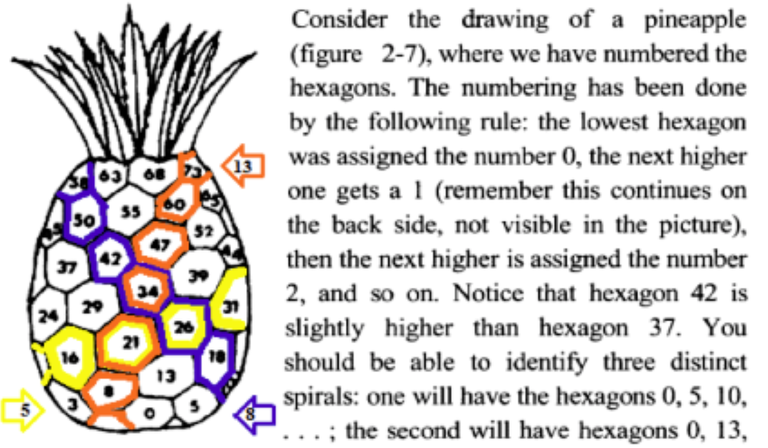
Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the Fibonacci Quarterly. Applications of Fibonacci numbers include computer algorithms such as the Fibonacci search technique and the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings,[11] such as branching in trees, phyllotaxis (the arrangement of leaves on a stem), the fruit sprouts of a pineapple,[12] the flowering of an artichoke, an uncurling fern and the arrangement of a pine cone's bracts.[13]

…

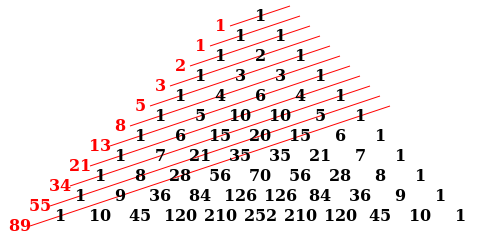
The Fibonacci numbers are the sums of the "shallow" diagonals (shown in red) of Pascal's triangle.

https://en.wikipedia.org/wiki/Golden_ratio

Retrieved: 12 November 2018
Archive: http://archive.fo/Zr44C

Golden ratio

In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. The figure on the right illustrates the geometric relationship. Expressed algebraically, for quantities a and b with a > b > 0,

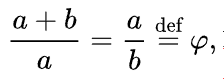
where the Greek letter phi (ϕ or φ) represents the golden ratio.[1] It is an irrational number with a value of:

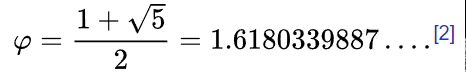
MES NOTE: This is the limit of the Ratio of Successive Numbers of the Fibonacci sequence in Exercise 4! #AbsolutelyAmazing!

The golden ratio is also called the golden mean or golden section (Latin: sectio aurea).[3][4][5] Other names include extreme and mean ratio,[6]medial section, divine proportion, divine section (Latin: sectio divina), golden proportion, golden cut,[7] and golden number.[8][9][10]

Mathematicians since Euclid have studied the properties of the golden ratio, including its appearance in the dimensions of a regular pentagon and in a golden rectangle, which may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has also been used to analyze the proportions of natural objects as well as man-made systems such as financial markets, in some cases based on dubious fits to data.[11] The golden ratio appears in some patterns in nature, including the spiral arrangement of leaves and other plant parts.

Some twentieth-century artists and architects, including Le Corbusier and Salvador Dalí, have proportioned their works to approximate the golden ratio—especially in the form of the golden rectangle, in which the ratio of the longer side to the shorter is the golden ratio—believing this proportion to be aesthetically pleasing.

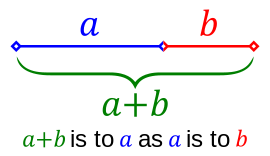
Line segments in the golden ratio

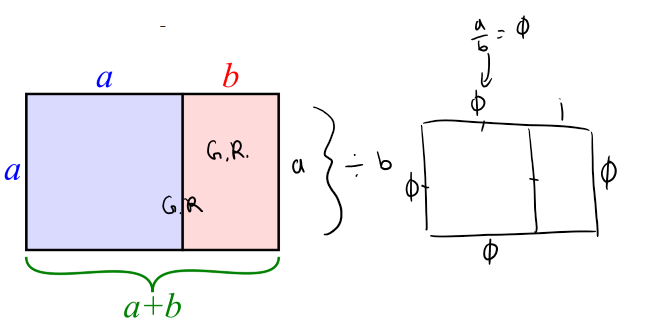
A golden rectangle with longer side a and shorter side b, when placed adjacent to a square with sides of length a, will produce a similar golden rectangle with longer side a + b and shorter side a.

…

Relationship to Fibonacci sequence

The mathematics of the golden ratio and of the Fibonacci sequence are intimately interconnected. The Fibonacci sequence is:

A closed-form expression for the Fibonacci sequence involves the golden ratio:

The golden ratio is the limit of the ratios of successive terms of the Fibonacci sequence (or any Fibonacci-like sequence), as originally shown by Kepler:[22]

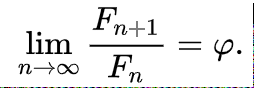
In other words, if a Fibonacci number is divided by its immediate predecessor in the sequence, the quotient approximates φ; e.g., 987/610 ≈ 1.6180327868852. These approximations are alternately lower and higher than φ, and converge to φ as the Fibonacci numbers increase…

MES Note:

φ = 1.61803398874989…

1/1 = 1
2/1 = 2
3/2 = 1.5
5/3 = 1.6667
8/5 = 1.6
13/8 = 1.625
21/13 = 1.6154
34/21 = 1.619
55/34 = 1.6176
89/55 = 1.6182
144/89 = 1.618
233/144 = 1.6181
377/233 = 1.618
610/377 = 1.618 …. My Built-In One Note Calculator Rounds Up.
φ = 1.61803398874989…

https://en.wikipedia.org/wiki/Golden_angle

Retrieved: 12 November 2018
Archive: http://archive.fo/w6c14

Golden angle

In geometry, the golden angle is the smaller of the two angles created by sectioning the circumference of a circle according to the golden ratio; that is, into two arcs such that the ratio of the length of the larger arc to the length of the smaller arc is the same as the ratio of the full circumference to the length of the larger arc.

Algebraically, let a+b be the circumference of a circle, divided into a longer arc of length a and a smaller arc of length b such that

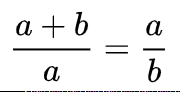
The golden angle is then the angle subtended by the smaller arc of length b. It measures approximately 137.5077640500378546463487 ...° A096627 or in radians 2.39996322972865332 ... A131988.

The name comes from the golden angle's connection to the golden ratio φ; the exact value of the golden angle is

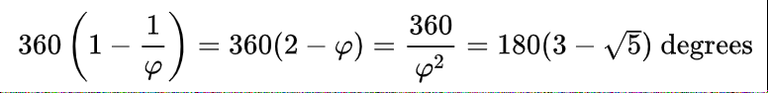
or

where the equivalences follow from well-known algebraic properties of the golden ratio.

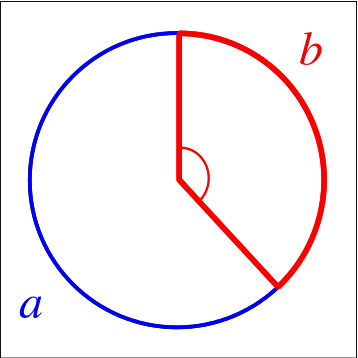
The golden angle is the angle subtended by the smaller (red) arc when two arcs that make up a circle are in the golden ratio

…

The angle between successive florets in some flowers is the golden angle.

https://en.wikipedia.org/wiki/Golden_spiral

Retrieved: 12 November 2018
Archive: http://archive.fo/N5whw

Golden spiral

In geometry, a golden spiral is a logarithmic spiral whose growth factor is φ, the golden ratio.[1] That is, a golden spiral gets wider (or further from its origin) by a factor of φ for every quarter turn it makes. A golden spiral with initial radius 1 has the following polar equation:

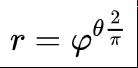
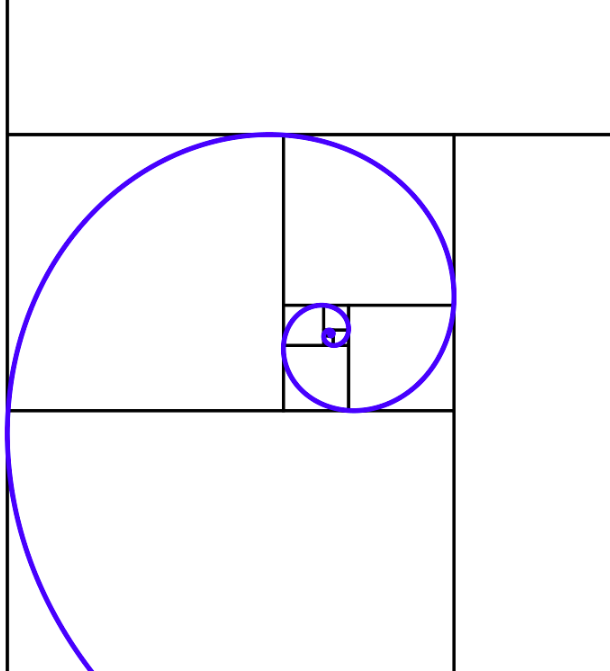
Golden spiral. Assuming a square has the side length of 1, the next smaller square is 1/φ wide. The next width is 1/φ², then 1/φ³, and so on.

…

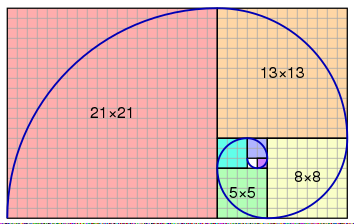
A Fibonacci spiral approximates the golden spiral using quarter-circle arcs inscribed in squares of integer Fibonacci-number side, shown for square sizes 1, 1, 2, 3, 5, 8, 13 and 21.

Some Golden / Fibonacci spirals in nature, art, design, corporations, and even advertising!

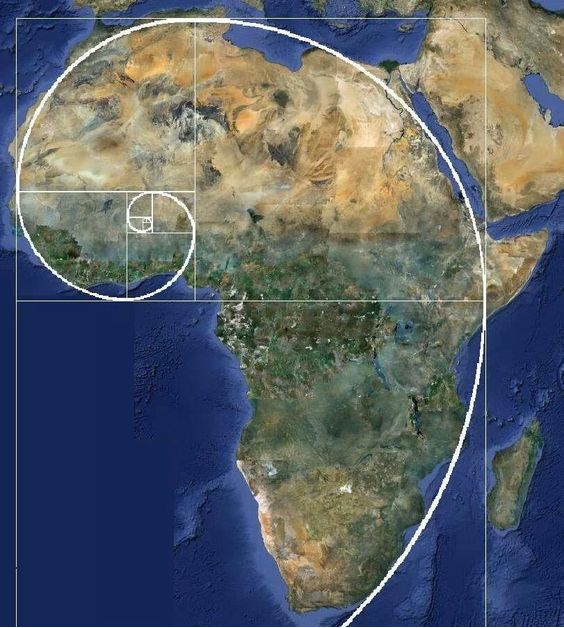
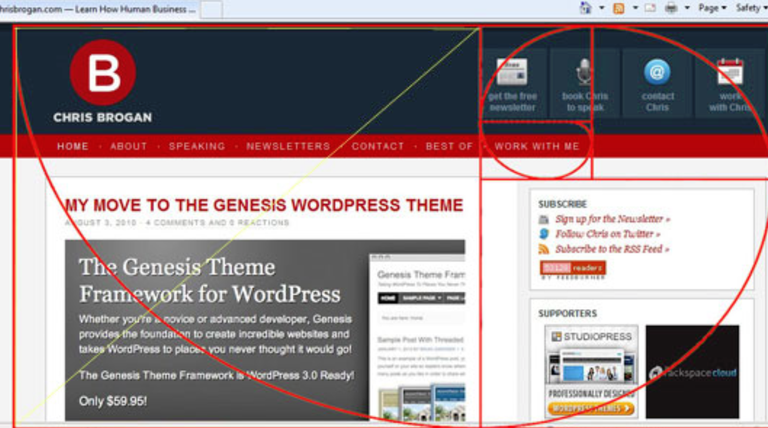
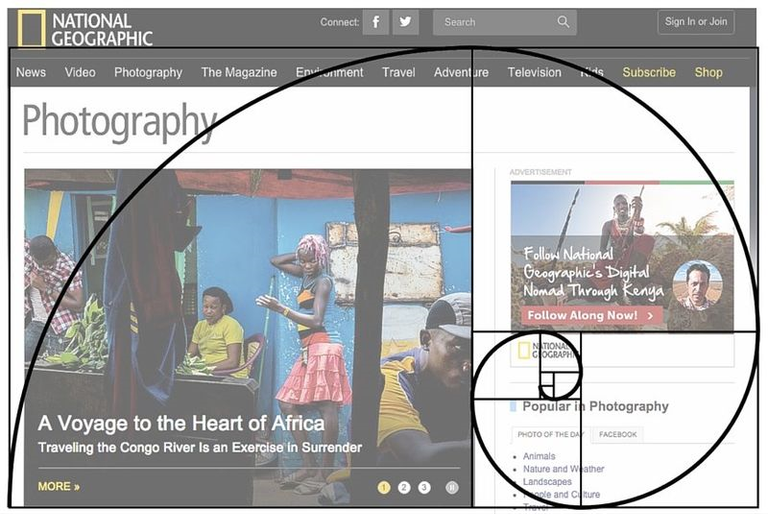
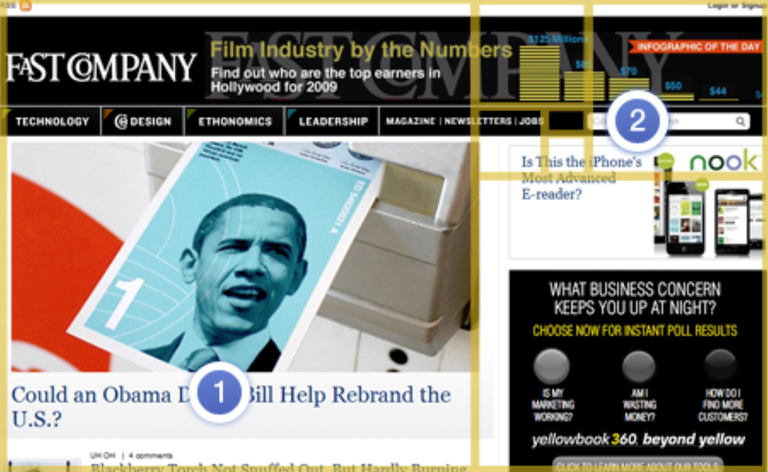
Pretty Cool Stuff!!

mathematics science sequences steemiteducation steemstem
0
0
0.000
0 comments