Shamir's Secret Sharing or How to Enforce Cooperation
Idea of Secret Sharing
Secret sharing is about sharing a piece of information among a certain set of people (N) and none of the people can get the complete information alone. A simple example is the following. A bank wants to secure its largest safe with a code. There must always be employees present who can open the safe but none of the employees should be able to do this alone. So the code can be distributed to all employees (N), so that at least (M) employees have to cooperate to open the safe. This simple example already shows how valuable such a Secret Sharing scheme can be.
Mathematics for Secret Sharing
One of the oldest and best known methods for secret sharing is probably Shamir Secret Sharing. This is simple, but it also requires a bit of mathematics. First of all, the definition of a polynomial must be clarified. A polynomial is a sum of powers of an unknown variable, where each power is preceded by a coefficient. In the formula below, the coefficients are marked with the letter a, while the variable has the letter x.
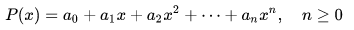
A simple polynomial (of degree n).
A polynomial in which the highest power of the variable is n is called a polynomial of degree n. Now there are two more facts we need to know about polynomials:
1.) If we know n+1 points on a polynomial of degree n, the polynomial is uniquely defined by these points.
2.) If we know n+1 points on a polynomial of degree n, then we can reconstruct the polynomial by these points alone.
Shamir's Secret Sharing
This is exactly what Shamir's secret sharing is based on. First, it is determined how many parties should cooperate to reconstruct the secret. So if I want to make sure that 3 parties can reconstruct a secret, I choose a polynomial of degree two. This has the following form:
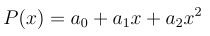
A polynomial of degree 2.
At a0 it is the secret that I want to distribute. However, all persons receive an arbitrary point on the curve. For example, person one gets P(1), person 2 gets P(2), and so on. Of course, a single point is not sufficient to determine a0 (i.e. P(0)). But if there was a way to determine the whole polynomial, also the secret could be determined! The polynomial can be found, for example, by solving a system of equations. This has the following form:
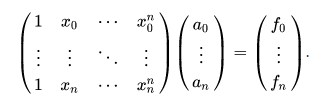
System of equations to find the polynomial.
By solving the system of equations, one finds the coefficients and thus the polynomial! Thus, in this example, three people can meet and solve the system of equations together with their part of the information called shares. Of course, there are more efficient methods for interpolation (e.g. Lagrange interpolation) and also other methods for secret sharing. But this is probably the simplest example.
Sources
[1] Adi Shamir. 1979. How to share a secret. Commun. ACM 22, 11 (Nov. 1979), 612–613. https://doi.org/10.1145/359168.359176
[2] Blakley, G.R., Kabatiansky, G. (2011). Secret Sharing Schemes. In: van Tilborg, H.C.A., Jajodia, S. (eds) Encyclopedia of Cryptography and Security. Springer, Boston, MA. https://doi.org/10.1007/978-1-4419-5906-5_389
Interesting, using a polynomial equation for a secret sharing event! I have never thought about that
!1UP
Click this banner to join "The Cartel" discord server to know more.
It's a simple yet brilliant idea in my opinion =D
You have received a 1UP from @gwajnberg!
@stem-curator, @vyb-curator, @pob-curator, @neoxag-curator, @pal-curator
And they will bring !PIZZA 🍕.
Learn more about our delegation service to earn daily rewards. Join the Cartel on Discord.
PIZZA Holders sent $PIZZA tips in this post's comments:
@curation-cartel(19/20) tipped @grider123 (x1)
Please vote for pizza.witness!
Very interesting idea with great applications. I've also heard of the zero-knowledge proof. BTW, remember to back up your post with sources. I think I suggested that once :)
Oh yeah forgot about that again -.-
I added the two most important sources =)
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.