Interpretación Geométrica de la Derivada
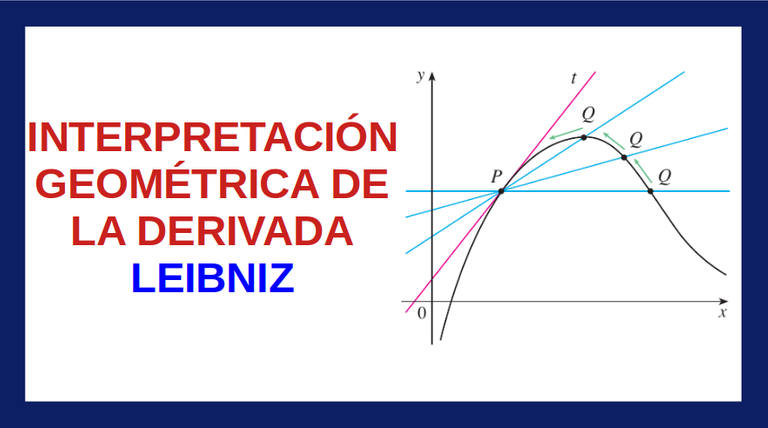
Hola amigos de Hive, el día de hoy vamos a ver la interpretación geométrica de una derivada.Ya vimos que físicamente representa una velocidad instantánea, pero ¿en el plano cartesiano?
Acompáñame
0
0
0.000
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Thanks for using the STEMsocial app and including @stemsocial as a beneficiary, which give you stronger support.
La pendiente de la recta que es tangente a la curva en cualquier punto = derivada. Gracias a Leibniz y Newton podemos contar hoy por hoy con esta super herramienta llamada derivada. Saludos y Gracias por compartir.
Muchas gracias por el apoyo.
Así es, estos dos grandes en matemáticas hicieron que avance la ciencia. Newton se le conoce por sus leyes, pero pocos conocían que en matemáticas tuvo grandes aportaciones.
Es impresionante ver como a medida que delta x se aproxima a cero, las rectas que inicialmente son secantes llegan hacer tangentes en un solo punto, que es lo que hoy en día conocemos como una tasa de variación instantánea. Gracias a Leibniz y Newton ciencias como la física avanzo a dar respuestas por ejemplo al cálculo de la velocidad y aceleración instantánea, y que por ejemplo teniendo una función de posición de una partícula, esta se puede derivar dos veces y obtenemos la aceleración del cuerpo en movimiento.
Es admirable el trabajo que viene desempeñando profesor, agradecido de poder contar con este material audiovisual, saludos.