Planos, rectas y vectores
Planos, rectas y vectores
En la solución del siguiente problema vamos a ver una serie de conceptos y principios básicos de geometría, trigonometría y vectores. La importancia de este problema es que exige el análisis cuidadoso de cada lugar geométrico como el plano y la recta y como ellos se relacionan en el espacio. He escogido este interesantísimo problema que he extraido del libro de Alonso M. y Finn E. J. ya que es bastante completo y es uno de los más consultados por los estudiantes de mis cursos de física 1.
Problema
Demostrar que la distancia entre la recta que pasa por el punto 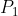

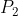
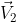
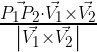
Solución
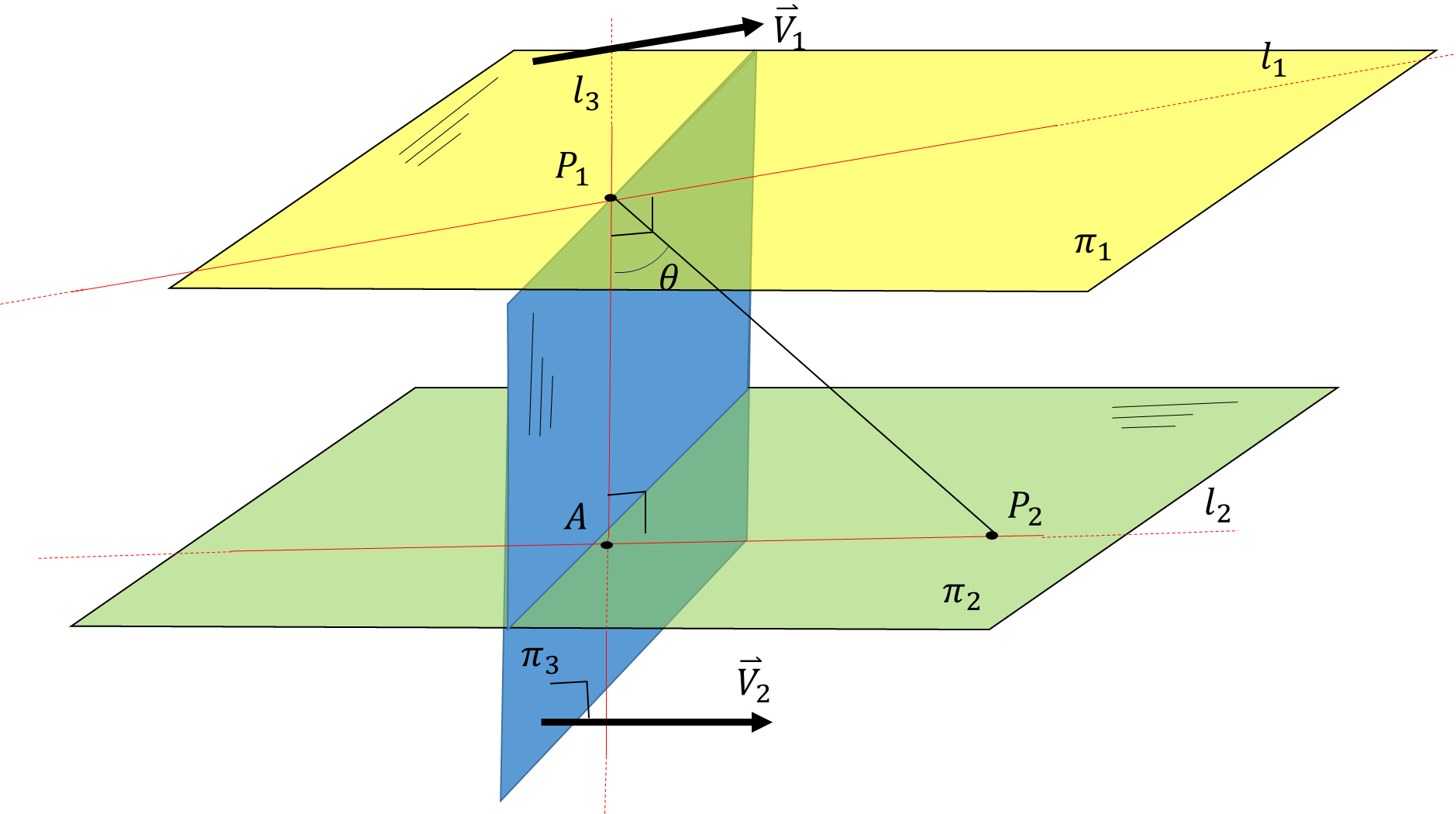
Para resolver este problema debemos saber que la distancia entre dos líneas que se cortan se definen como la longitud de la perpendicular más corta a ambas líneas. Acá vamos a utilizar las coordenadas de 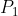
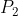

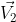
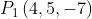




Figura 1. Interpretación geométrica del enunciado del problema.
Si dos rectas en el espacio son paralelas cualquier segmento perpendicular perpendicular a ambas rectas será la distancia entre ellas, pero si no son paralelas, sólo y sólo un segmento será perpendicular entre ambas rectas. ¿Cómo podemos hallar este segmento que indica la distancia entre dos rectas no paralelas? Según los datos del problema procederemos de la siguiente manera.
Hallemos el producto vectorial entre 
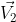
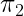
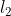
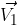
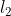
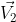
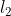
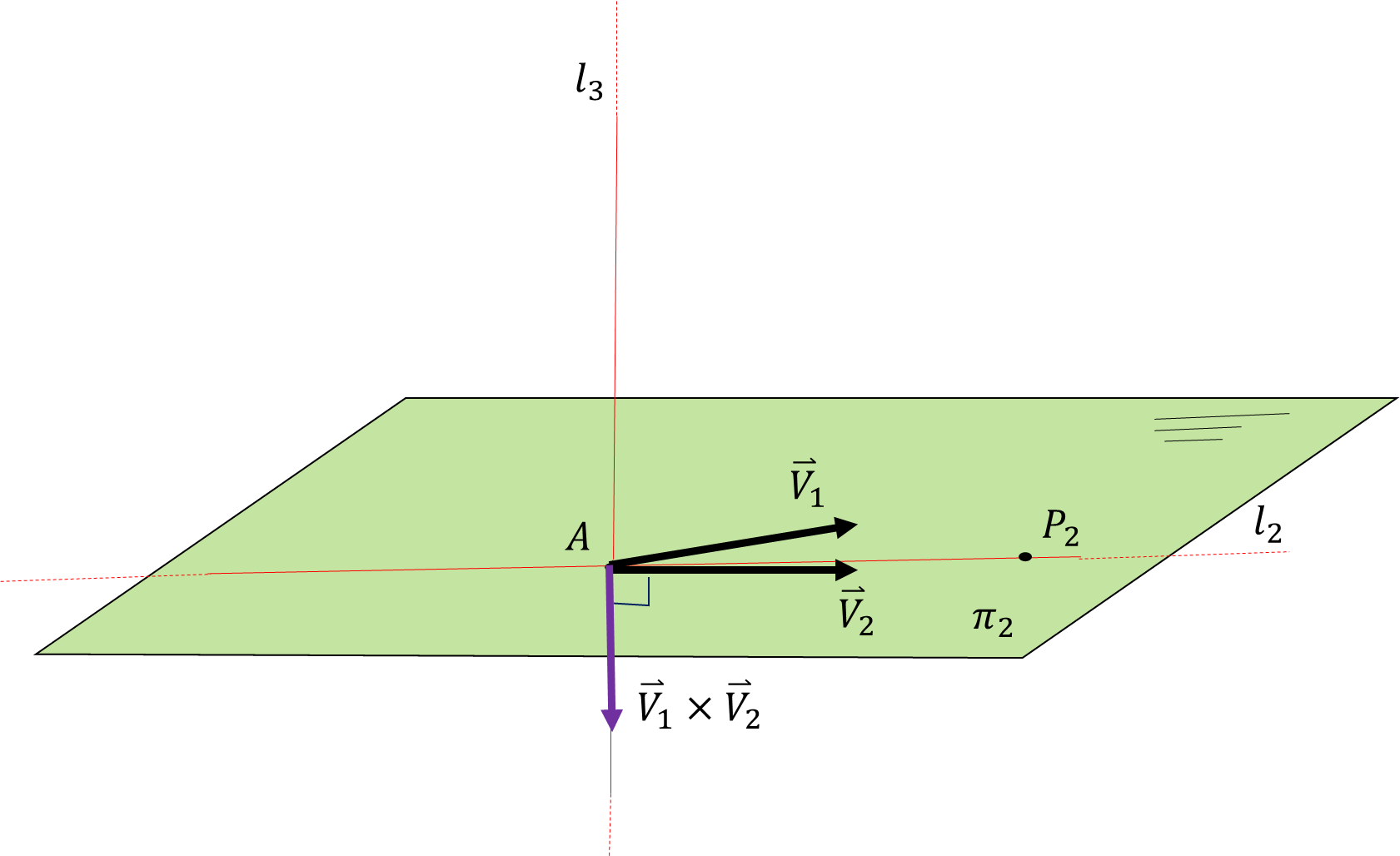
Figura 2. Producto vectorial de 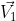 y
y  en el plano
en el plano 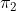 .
.
Podemos observar que 
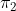

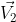
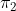
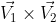
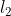

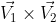
Ahora necesitamos que 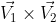

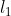
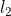
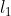
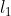
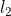

Pueden haber infinitas rectas que son perpendiculares a 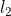
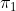
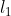
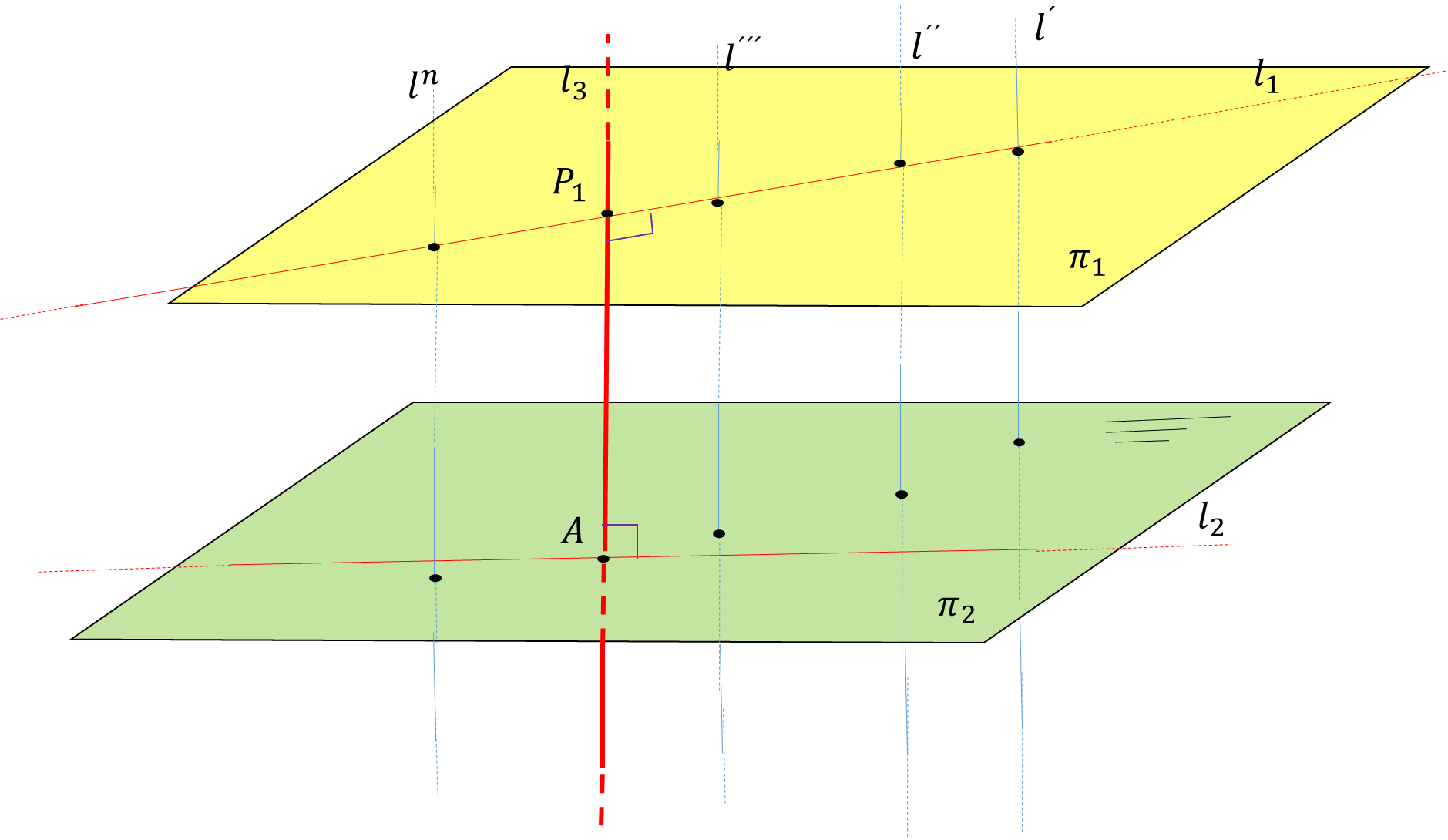
Figura 3. Distintas rectas perpendiculares a  y a
y a  que también son perpendiculares a
que también son perpendiculares a  . las rectas
. las rectas 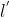 ,
,  ,
, 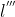 , ...,
, ..., 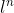 son perpendiculares a
son perpendiculares a 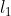 ,
, 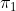 y
y 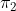 , pero no intersectan a ningún punto de la recta
, pero no intersectan a ningún punto de la recta 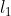 , pero
, pero 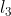 intersecta a
intersecta a 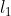 y además ambas son perpendiculares.
y además ambas son perpendiculares.
Los puntos de intersección de la recta 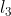
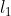
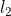
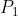
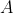
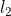
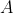
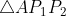
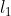
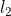

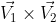
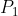
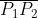
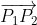
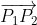
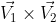
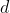
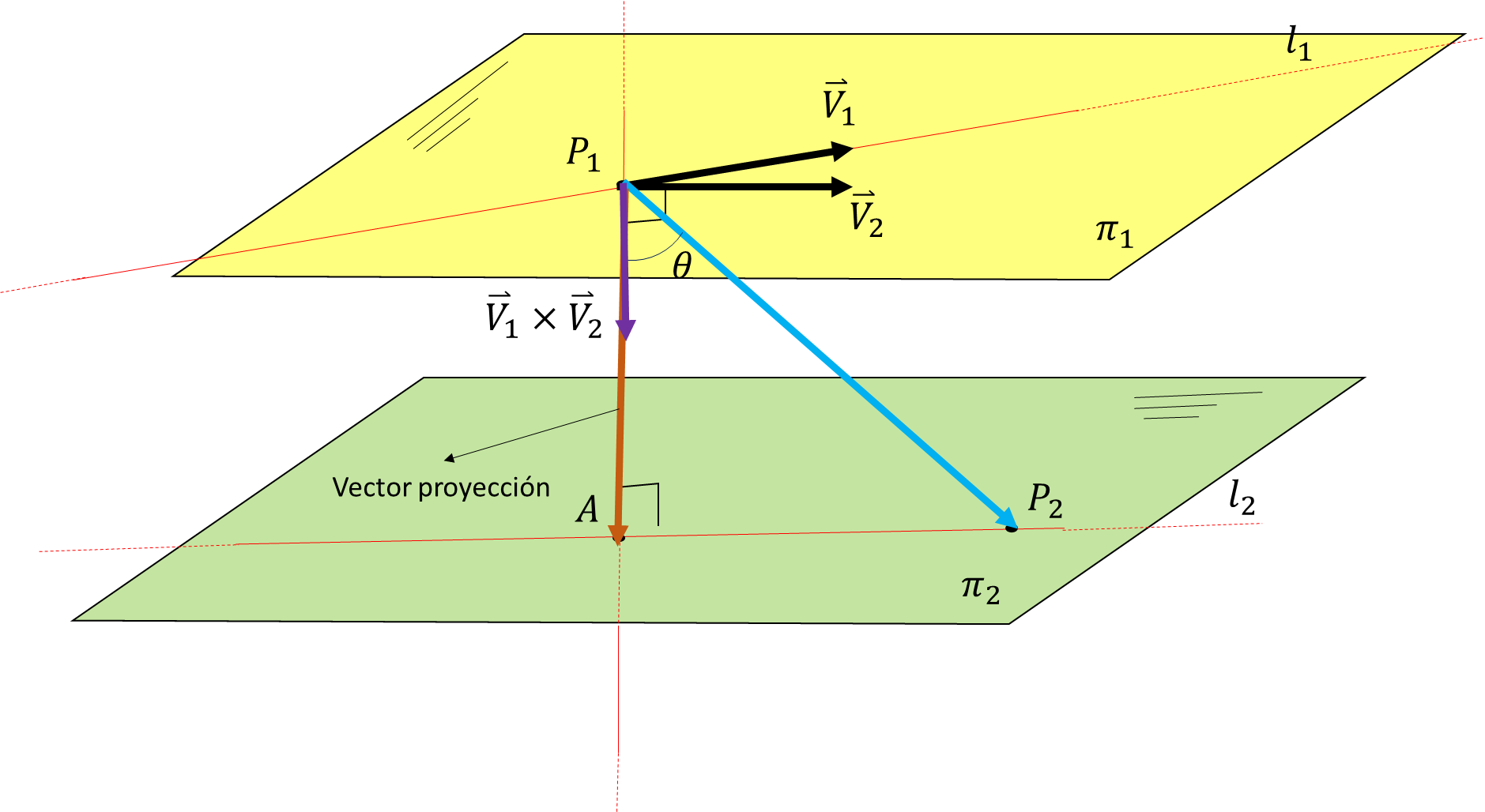
Figura 4. El vector 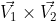 trasladado al punto
trasladado al punto 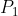 .
.
Entonces procedamos a realizar los cálculos.
Vector proyección de 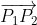
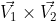

La magnitud del vector proyección es

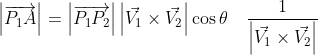
Por la definición de producto escalar podemos escribir la expresión anterior de la siguiente manera
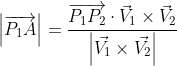
donde 

Ahora si 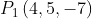
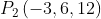

luego



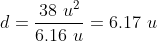
Por lo tanto la distancia entre las rectas 

Conclusiones
Con la solución de este problema hemos puesto a prueba una vez más el poder de la geometría, trigonometría y el análisis vectorial. El planteamiento del problema en principio parece muy elemental y básico, sin embargo, como pudimos ver su solución requiere de una interpretación correcta de los lugares geométricos o elementos que se describen en el enunciado. Con su solución en detalle podemos ver que es bastante completo y nos obliga a analizar con cuidado cada interpretación que podamos dar a la hora de solucionarlo.
Fuentes bibliográficas
Finn E. J., Alonso M., Física Vol I: Mecánica. Fondo Educativo Interamericano, México, 1971
Sears F. Zemansky, Young H., Freeman R. Física universitaria, 11ra. Ed., Volumen I, Pearson Addison Wesley, México, 2004.
Brand Louis, Análisis vectorial. C.E.C.S.A, México, 1975.
Fuentes de las imágenes
Todas las demás imágenes fueron hechas por mí usando en software Power Point.


Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (80% of the curation rewards are returned).
Please consider including @stemsocial as a beneficiary to get a stronger support.
Your content has been voted as a part of Encouragement program. Keep up the good work!
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more