Determination of the equation of a parabolic shot and calculation of the best angle for its execution

How many of these types of parabolic movements can we see around us, surely many, that's why this time we move to basketball where you can see the beautiful parabola described by the ball being thrown by the players to the basket, therefore, physical science and mathematics can be used everywhere where we are, then my dear friends to continue expanding our knowledge in relation to the phenomenon of movement, especially the parabolic, then I leave you the following approach or statement.
Exercise
A basketball player makes a shot with a ball towards a basket, the player is at a distance of 6.25 meters (m) from the basket, the height at which the ball went out was 2.35 meters (m) and whose initial speed was 10 m / s, the height of the hoop that holds the mesh is 3.05 meters (m), therefore, in relation to the above answer the following questions:
a.- What is the equation of the trajectory of the parabolic launch?
b.- What is the best angle for the player to get the ball into the basket?
Solution
Data:
Vo = 10 m/s (Initial bolon velocity).
g = 9,8 m/s2. (Gravity)
X = 6,25 m (Distance of the ball throw).
HL = 2,35 m (Throwing height of the ball).
Ha = 3,05 m (Hoop height).
Y = Ha - HL = 3,05 – 2.35 = 0,70 m.
θ = ? (Launch angle).
a.- To begin answering our first question, we will start by visualizing the following figure 1.

We then identify the formulations to be used, thus, we have the following formula 1.

For formulation 1 above, we need to describe the variables that identify time, and for this we have:
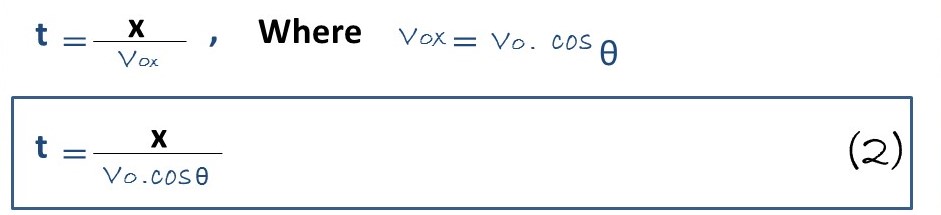
Now we substitute the algebraic value of time (t) into equation 1.

In this way we obtain the formula 3, which represents the equation of the trajectory of the parabolic throw made by the basketball player observed in the gif of the presentation of this article.
b.- After constructing the equation of the parabolic trajectory of the ball, we proceed to answer our second question, i.e., what will be the best angle for the parabolic launch, and which will give the player the best chance of scoring the ball, then, we proceed as follows.

When applying our parabolic trajectory equation we notice that we obtain a second degree equation, therefore, we proceed as follows in order to find the best angle of shot for the player.

From this handle we obtain two draft angles, one of 70.22° and the other of 26.10°, so that, in this case, the best angle will be the one of 70.22° because it provides a higher launch than the angle of 26.10° can provide.
Conclusion
The human being performs a large number of activities, where any kind of movement is developed, especially in sports disciplines such as basketball, and we were able to prove this in this opportunity, and we were also able to link it with physical science and mathematics by determining the equation that describes the parabolic trajectory of the shot when it is thrown towards the basket.
We also managed to calculate two shooting angles by using the equation of the parabolic trajectory described above, and we analyzed how the most advisable angle is the one of 70.22° because it will allow a greater elevation of the ball towards the hoop, and with the other angle the shot would go straighter without the necessary inclination to reach the height of the hoop, a wonderful example of the implementation of parabolic motion using the physical-mathematical interpretation to find important applications in basketball and certainly in any other sport.
Until another opportunity my dear friends.
Note: The images were created by the author @rbalzan79 using Power Point and Paint, the animated image was created using the PhotoScape application.
Recommended bibliographic references
[1] Parabolic Projectiles. Link.
[2] El movimiento rectilíneo. Link.
[3] Projectile Motion. Link.
thanks for the class !1UP
Thanks to you for your support. Best regards.
You have received a 1UP from @gwajnberg!
@ccc-curator, @stem-curator, @neoxag-curator
And they will bring !PIZZA 🍕.
Learn more about our delegation service to earn daily rewards. Join the Cartel on Discord.
Thank you for your valuable support. Best regards.
I gifted $PIZZA slices here:
@curation-cartel(4/20) tipped @rbalzan79 (x1)
Please vote for pizza.witness!
Thank you for your support. Regards.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Thank you dear @Stemsocial community for your support. Regards.
And sportspeople think math won't help them! :P
Hello, yes, mathematics is the most universal language that we know as humanity and that has given us so much interpretation on any phenomenon that develops around us, thank you for your valuable visit and comment. Greetings.
Congratulations your publication has been chosen among the best of the day.
KEEP CREATING GOOD CONTENT.
Thanks for the support @edu-venezuela.