Calculation of the travel speed of an acoustic signal receiver / Cálculo de la velocidad de desplazamiento de un receptor de señal acústica (ENG-ESP)

First condition: Receiver immobile, and sound emitting focus in motion.
Second condition: Receiver in motion, and sound emitter immobile.
Third condition: Receiver and emitter of sound, both in motion.
These three conditions analyzed with the purpose of knowing the frequency perceived by the receiver of any acoustic signal, using the formulation for such phenomenon of the Doppler effect, however, with this formula we can calculate other variables present, being one of them to calculate the speed of the element that receives a certain acoustic signal, and in this calculation we will focus in this opportunity, to continue knowing more about this intrinsic phenomenon present in the propagation of sound, and for this, of course, we will use again the general formulation of the Doppler effect, to clear the variable required in this occasion.
Exercise
An old fighter plane is moving normally, when suddenly it receives an acoustic signal from outside with a frequency of 4,150 Hz, with the purpose of informing it that a storm is approaching, this signal comes from an air control tower located on the ground, and which emits the acoustic signal at a frequency of 4,850 Hz, having as logic, that these sound waves propagate through the most common material medium on our planet, the air, at a speed of 340 m/s. Therefore, in relation to the above described answer the following questions:
a.- Is the aircraft moving away from or towards the air traffic control tower issuing the alert signal?
a.- What is the speed at which the aircraft is traveling?
Solution
We will start by pointing out the general formula of the Doppler effect, with the description of each of its variables:

fr = It is the frequency of the sound perceived by the receiver.
fo = Represents the sound frequency of the emitting source.
Vm = Velocity of the sound propagation medium (air in this case)
VR = Receiver speed.
Vf = Speed of the sound emitting source.
For this opportunity we will implement this formula for the calculation of the speed of the receiver of the acoustic signal, and not as in other occasions that we use it to know the frequency perceived by the receiver under the three previous conditions described, that is, to know another application of this formulation, so let's start with our purpose raised.
a.- Data:
fr = 4.150 Hz.
fo = 4.850 Hz.
Vm = 340 m/s.
Based on these three important data, we can clearly notice that the frequency received by the airplane (4,150 Hz) is lower than the frequency emitted by the emitting source of the acoustic signal, this makes us deduce, as previously expressed by the Doppler effect, that the plane is moving away from the control tower which emits the acoustic message.
Recall again that the Doppler effect causes the receiver of a sound to receive a frequency different from the frequency emitted by a particular sound emitting focus, this perceived frequency may be higher or lower than the emitted frequency, so if it is higher, we say that the receiver is approaching the source of sound emission, and the opposite occurs when it moves away, from this point of view, clearly we note that the frequency received is lower(4. 150 Hz < 4,850 Hz), therefore, the aircraft is moving away from the control tower, so it must return before the weather worsens.
This first question is another example related to the second condition already analyzed, where the receiver is moving and the transmitter is motionless, and it was necessary to begin to answer this question to clarify the type of sign to use in the resolution of the second unknown, therefore, as it has been expressed, that the plane is moving away from the control tower, we will use the minus sign (-) in the equation (1), being thus:

From the formula (2) we have that the velocity of the emitting focus is zero, because it is static, being as follows:

b.- To answer this question it is important to proceed to clear the RV, from the formula (3) as you can see:
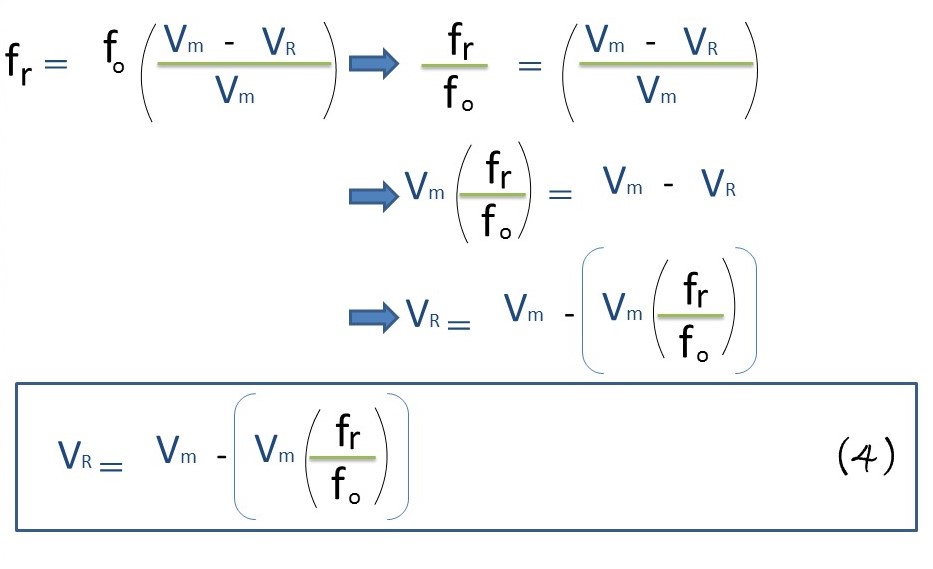
Using formula 4, we proceed to substitute the known variables and obtain the aircraft velocity (VR) which represents the receiver of the acoustic signal.

This is the speed of the aircraft at the moment of receiving the acoustic signal, and that, in addition, it was moving away from the air traffic control tower, so it had to be returned to safety.
Analysis of results
After the analysis of the three conditions described above, it was necessary to extend the application of the Doppler effect formulation, as happened in this opportunity through the calculation of the speed of the receiver of the acoustic signal, which in this case was an airplane and which was moving away from the air traffic control tower when it received the warning message, the phenomenon of the Doppler effect can be found in different circumstances, although in many occasions we do not stop despite its application.
It is certain that through the formulation of this phenomenon we will be able to further analyze other variables, beyond the frequencies perceived by the receiver of the sound, and the speed of the receiver of the acoustic signal, analyzed on this occasion, by means of the formulation (4).
Until another opportunity my dear friends.
Note: The images were made by the author using Power Point and Paint, and the gif image was made with PhotoScape.
Recommended Bibliographic References
[1] MOVIMIENTO ONDULATORIO. Link.
[2] Doppler Effect. Link.
Spanish version

Primera condición: Receptor inmóvil, y foco emisor de sonido en movimiento.
Segunda condición: Receptor en movimiento, y emisor de sonido inmóvil.
Tercera condición: Receptor y emisor de sonido, ambos en movimiento.
Estas tres condiciones analizadas con la finalidad de conocer la frecuencia percibida por el receptor de cualquier señal acústica, utilizando la formulación para tal fenómeno del efecto Doppler, sin embargo, con esta fórmula podemos calcular otras variables presentes, siendo una de ellas calcular la velocidad del elemento que recibe una determinada señal acústica, y en este cálculo nos centraremos en esta oportunidad, para seguir conociendo más sobre este intrínseco fenómeno presente en la propagación del sonido, y para ello, por supuesto, utilizaremos nuevamente la formulación general del efecto Doppler, para despejar la variable requerida en esta ocasión.
Ejercicio
Un antiguo avión de combate se desplaza en total normalidad, cuando de repente recibe una señal acústica del exterior con una frecuencia de 4.150 Hz, con la finalidad de informarle que se avecina una tormenta, dicha señal proviene de una torre de control aéreo ubicada en tierra, y la cual emite la señal acústica a una frecuencia de 4.850 Hz, teniendo como lógica, que estas ondas sonoras se propagan por el medio material más común en nuestro planeta, el aire, a una velocidad de 340 m/s. Por lo tanto, en relación a lo antes descrito responder a las siguientes interrogantes:
a.- ¿El avión se aleja o se acerca a la torre de control aéreo que emite la señal de alerta?
a.- ¿Cuál es la velocidad a la que se desplaza el avión?
Solución
Comenzaremos señalando la fórmula general del efecto Doppler, con la descripción de cada una de sus variables:

fr = Es la frecuencia del sonido percibida por el receptor.
fo = Representa la frecuencia del sonido del foco emisor.
Vm = Velocidad del medio de propagación del sonido (El aire en este caso)
VR = Velocidad del receptor.
Vf = Velocidad del foco emisor del sonido.
Para esta oportunidad implementaremos dicha fórmula para el cálculo de la velocidad del receptor de la señal acústica, y no como en otras ocasiones que la utilizamos para conocer la frecuencia percibida por el receptor bajos las tres anteriores condiciones descritas, es decir, conocer otra aplicación de esta formulación, así que comencemos con nuestro propósito planteado.
a.- Datos:
fr = 4.150 Hz.
fo = 4.850 Hz.
Vm = 340 m/s.
Basado en estos tres importantes datos, podemos notar claramente que la frecuencia recibida por el avión (4.150 Hz) es menor que la frecuencia emitida por el foco emisor de la señal acústica, esto nos hace deducir, según lo antes expresado por el efecto Doppler, que el avión se aleja de la torre de control la cual le emite el mensaje acústico.
Recordemos nuevamente que el efecto Doppler hace que el receptor de un sonido reciba una frecuencia distinta a la frecuencia emitida por un determinado foco emisor de sonido, esta frecuencia percibida puede ser mayor o menor a la frecuencia emitida, por lo que si es mayor, decimos que el receptor se acerca a la fuente de emisión de sonido, y lo contrario ocurre cuando se aleja, desde este punto de vista, claramente notamos que la frecuencia recibida es menor(4.150 Hz < 4.850 Hz), por lo tanto, el avión se aleja de la torre de control, por lo que deberá regresar antes que el tiempo climático empeore.
Esta primera interrogante, es otro ejemplo relacionado a la segunda condición ya analizada, donde, el receptor está en movimiento y el emisor inmóvil, y era necesario comenzar a responder esta interrogante para clarificar el tipo de signo a utilizar en la resolución de la segunda incógnita, por lo tanto, como se ha expresado, que el avión se aleja de la torre de control, utilizaremos el signo menos (-) en la ecuación (1), quedando así:

De la fórmula (2) tenemos que la velocidad del foco emisor es cero, por estar estático, quedando de la siguiente manera:

b.- Para responder a esta interrogante es importante proceder a despejar la VR, de la fórmula (3) como pueden ver:

Utilizando la fórmula 4, procedemos a sustituir las variables conocidas y obtener la velocidad del avión (VR) el cual representa el receptor de la señal acústica.

Esta es la velocidad del avión al momento de recibir la señal acústica, y que, además, se estaba alejando de la torre de control de tráfico aéreo, por lo que se tenía que devolver para su resguardo.
Análisis de los resultados
Luego de los análisis de las tres condiciones antes descritas, era necesario poder ampliar la aplicación de la formulación del efecto Doppler, como ocurrió en esta oportunidad a través del cálculo de la velocidad del receptor de la señal acústica, que en este caso era un avión y el cual se estaba alejando de la torre de control de tráfico aéreo cuando recibió el mensaje de alerta, el fenómeno del efecto Doppler podemos encontrarlo en distintas circunstancias, a pesar que en muchas ocasiones no nos detenemos a pesar de su aplicación.
De seguro que a través de la formulación de este fenómeno podremos más adelante seguir analizando otras variables, más allá, de las frecuencias percibidas por el receptor del sonido, y de la velocidad del receptor de la señal acústica, analizadas en esta ocasión, por medio de la formulación (4).
Hasta otra oportunidad mis queridos amigos.
Nota: Las imágenes fueron realizadas por el autor utilizando Power Point y Paint, y la imagen gif realizado con PhotoScape.
Referencias Bibliográficas recomendadas
[1] MOVIMIENTO ONDULATORIO. Link.
[2] Doppler Effect. Link.
Su post ha sido valorado por @ramonycajal
Gracias por tan valioso apoyo a toda la comunidad de @Cervantes. Saludos.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Thank you dear community for your valuable support. Best regards.
awesome example was used in here! thanks for the exercise

!1UP
Thank you for your visit and valuable comment. Best regards.
You have received a 1UP from @gwajnberg!
@ccc-curator, @stem-curator, @neoxag-curator
And they will bring !PIZZA 🍕.
Learn more about our delegation service to earn daily rewards. Join the Cartel on Discord.
Thank you for your support.
Salut, je mettais de côté pour un nouveau vélo de route depuis un moment, mais les prix en magasin étaient toujours trop élevés. Un collègue m'a recommandé win hero casino, en mentionnant leurs bonus adaptés aux joueurs français. Le début a été compliqué, une série de petites pertes m'a presque découragé. J'ai finalement décidé de risquer un pari un peu plus élevé sur un jeu à thème cycliste et j'ai touché un gain énorme qui m'a permis d'acheter l'équipement dont je rêvais. Pour les personnes en France qui cherchent une opportunité supplémentaire, cet endroit en vaut la peine.