Greetings again my dear friends I hope you are all very well, the energy walks by our side in every moment where we are and, above all, it does so by our own physical entity, with which we can do any kind of work, in the most common that we can witness the action of energy, is in the form of kinetic energy, likewise the potential, of the latter we analyzed in a previous article the elastic potential energy.

Then we analyzed the work exerted by a certain friction force, where we noticed that this type of force is non-conservative, and this time the intention is to analyze the action of conservation of mechanical energy, therefore, this type of energy is the result of the addition of both the kinetic energy and potential energy of a given system.

Therefore, we can say that if the work done by all those non-conservative forces is null or zero, then the mechanical energy of a given body or system will remain constant. This law is the one we will use in the exercise to be analyzed below, so we can know the formulation of the relation of conservation of mechanical energy.

Once we have observed the previous formulation, we can move on to the statement of our exercise and, in this way, solve it with the help of our formula 1.

Exercise

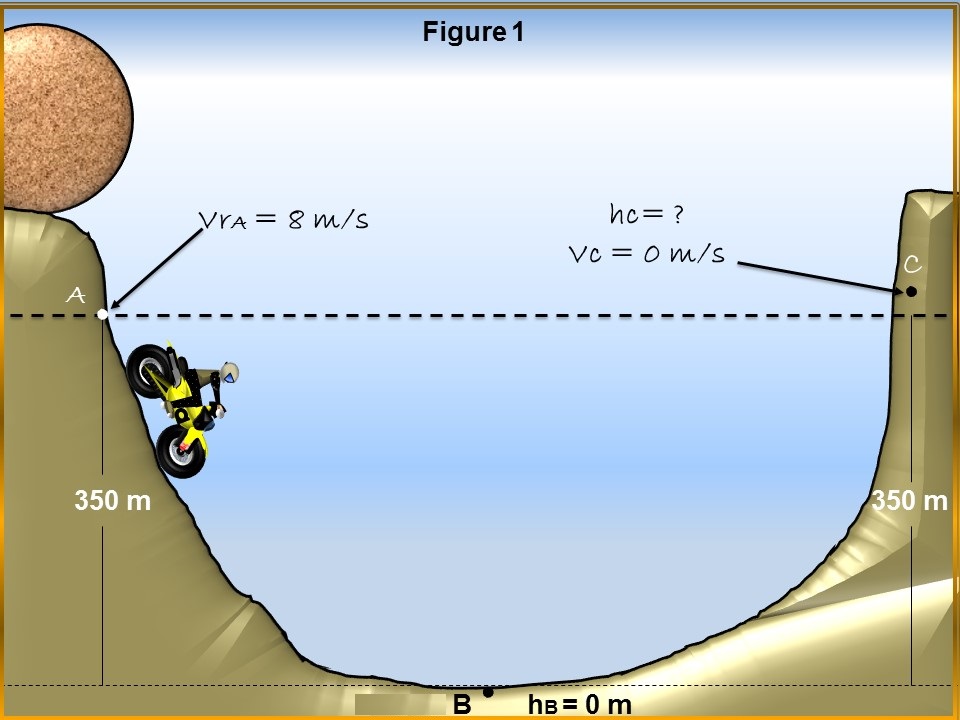
A daring motorcyclist wants to demonstrate that he is able to get out of the onslaught of a huge circular rock, which will be released behind him in a concave valley, the rock passing through point A, does so with a speed of 8 m / s, from the precise moment that the rock passes through the (Point A) to the lowest point of the valley, there is a distance of 350 m, in relation to the above described, answer the following questions:

a.- What will be the velocity of the huge rock at the moment of being at the lowest point of the valley, point (B)?

b.- To be safe from the huge rock, how high must the motorcyclist climb up the slope of the valley?

Data:
Vr(A) = 8 m/s (Rock velocity at point A).
hr(A) = 350 m (Rock height at point A).
Vr(B) = ? (Rock velocity at point B).
hB = 0 m (Rock height at point B)
Vc = 0 m/s (Rock velocity at point C)
hc = ? (Height of the motorcyclist to be safe from being hit by the rock).

Solution

a.- To begin the resolution of our first unknown, we must point out that the ball should obtain an increase in its kinetic energy since the non-conservative forces would have zero action, therefore, this increase in kinetic energy is due to the decrease in its gravitational power energy of the system analyzed between points A and B, thus conserving its mechanical energy, according to the above described, then, let us apply the law of conservation of mechanical energy.

Thus, we obtain the velocity that the rock had at the moment it was at the lowest point of the valley, that is, at point B, as shown in figure 1.

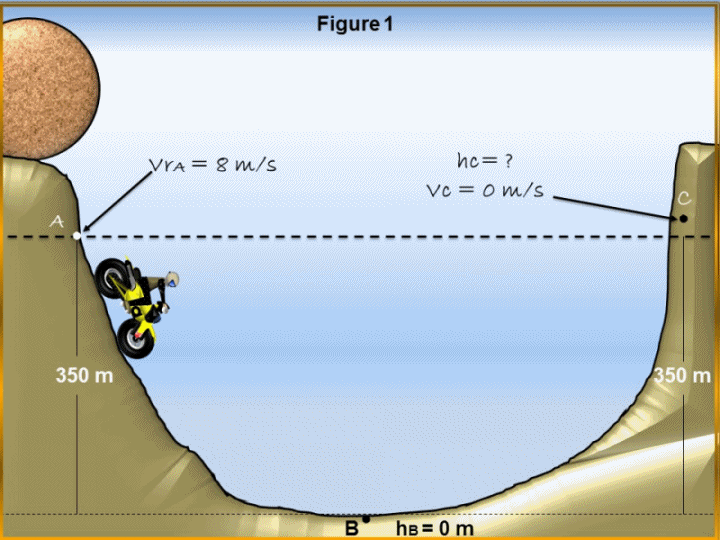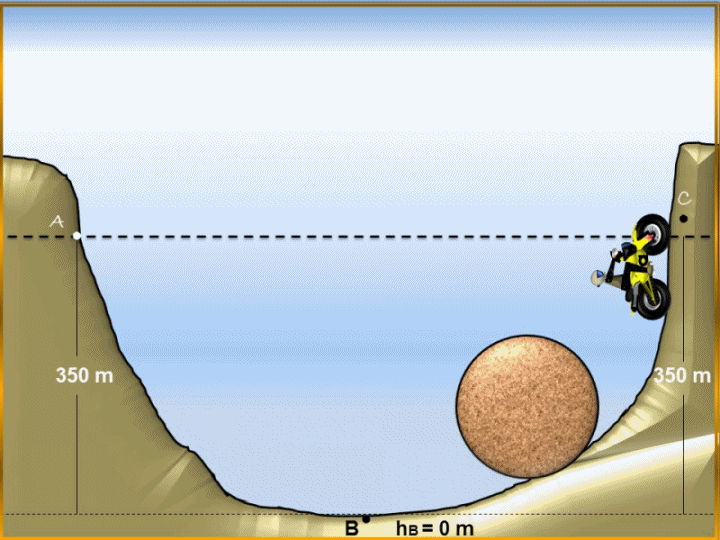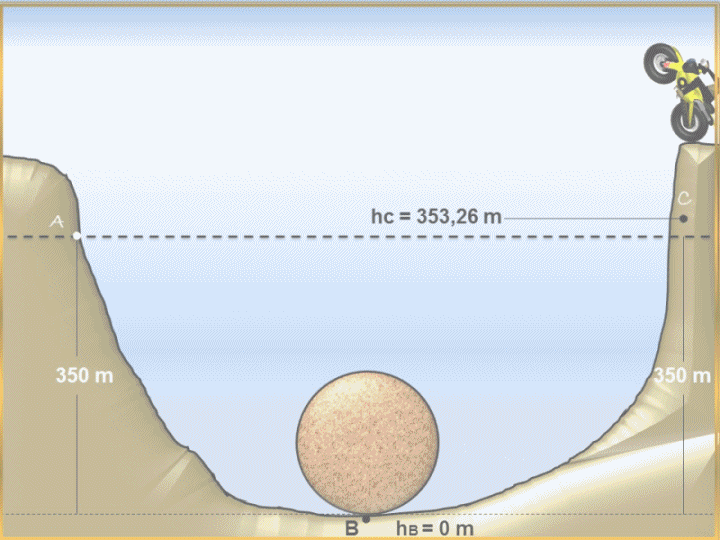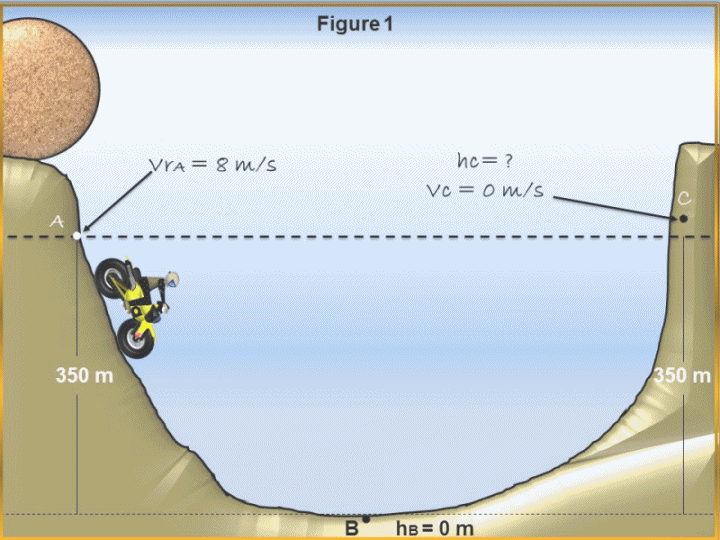
b.- Now we proceed to find the point or height at which the motorcyclist will be safe and avoid being run over by the huge rock, for this, the motorcyclist must continue driving his motorcycle until the rock has converted all its kinetic energy into potential energy and thus stop, therefore, we can express that the mechanical energy now in the system B and C is conserved.

In this way we obtain the height that the motorcyclist must obtain to be safe from being run over by the huge rock, since at this height the rock has already lost all its kinetic energy and transformed into potential energy, highlighting that at this point the speed of the rock is zero since it has stopped.

Conclusion

How much energy passes or is transformed in the different activities of man, that is why, the vital importance of knowing about them and thus take into account that through the various mathematical formulations can answer many questions that we can present daily, and this in any space-time where we find ourselves.

Through the law of conservation of mechanical energy, we have been able to analyze and answer the above questions, because the non-conservative forces in these systems were zero, therefore, the mechanical energy remained constant, there are many examples where we can apply this type of formulation as we did in this article, later we will continue to share the application of important mathematical formulations in order to understand various phenomena that develop around us.

Until another opportunity my dear friends.

Note: The images were created by the author using Power Point, the animated gif was created using the PhotoScape application.

Recommended Bibliographic Reference

[1] Conservation of Mechanical Energy . Link.