Greetings again my dear friends I hope you are all well, how much activity we do every day to meet any challenge we have to assume, that has been one of the most outstanding feature of humanity and, with which we continue to have for the benefit of our development in full and, whose fundamental engine has been the field of science-technology, which is why, where we go or we are all will be permeated by the action and influence of science.

In this opportunity I will continue with the proposed purpose which is none other than to continue highlighting the importance of the usefulness of any algebraic expression or mathematical formulation in our countless activities, this time linked to the route of a fire vehicle which will travel a road whose trajectory is varied, but usually curvilinear, if there is an action that accelerates our adrenaline is the speed, especially in the curves.

In the previous article we talked about satellites and one of their routes, such as the circular, and how to deny the great impact on our development of these machines or artificial spacecraft, but also the creation of the automobile has been another of those great inventions of great utility for our dizzying growth as humanity, since in this way we have moved by land more quickly from one place to another and, by different routes.

Without further details, I would like to share with you the following practical exercise and see how we can apply some mathematical formulas linked to the second law of the great Isaac Newton, so I hope you can learn something about it.

Exercise

A fire station receives an emergency call and, the people of that firefighting unit go to that call through their fast vehicle, during the journey or route the driver knows that the road or highway is structured of several curvilinear sections, for example; Some sections are curved-flat and others are curved-inclined, by virtue of the aforementioned characteristics, we have that the coefficient of friction (μ) that exists between the road and the wheels of a firefighter car is 0.25, this applied in the curvilinear-flat section, whose radius of curvature is 22 meters (m), the vehicle must also pass through another curvilinear section, but, with inclination, in the second section the vehicle manages to reach a speed of 120 Km/h, where the radius of curvature of said curvilinear-inclined section is 105 meters (m), therefore, in relation to what has been expressed above, answer the following questions:

a.- What would be the maximum speed that the vehicle can reach when going through the curvilinear-flat section without skidding or sliding and be able to reach the aid?

b.- What is the angle of inclination in the curvilinear-inclined section which prevents the vehicle from sliding and losing control despite a considerable speed of 120 km/h?

Solution

a.- Let's see what data we have to resolve our first question:

Data:

μ = 0,25 (Coefficient of friction).
r = 22 m (Radius of curvature in curvilinear-flat section).
V = ? (Maximum speed to be able to pass the indicated section).

Once we have pointed out the data offered, it is important to highlight that we will implement as a basis for the resolution of this and the second unknown the second law of Newton, related to the sum of the forces both in the horizontal axis (X) and in the vertical axis (Y).

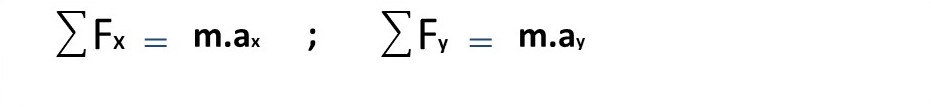
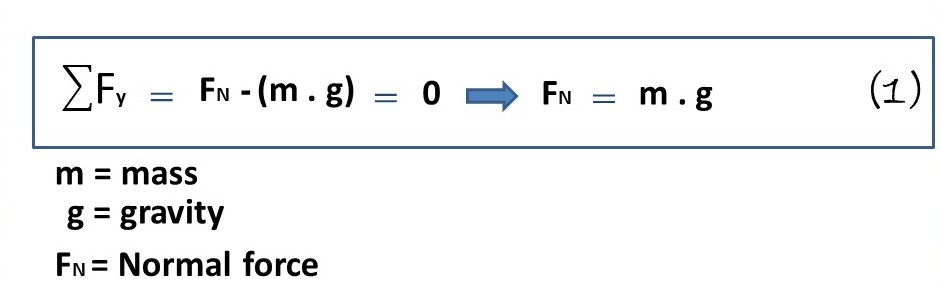
By virtue of the previous relation, we can express that in the vertical axis (Y), we find both the gravitational force and the normal force, and, that in this axis there is no acceleration, therefore, there is no acceleration:

It is important to say that the friction force between the wheels of the car and the road provides the necessary radial force to maintain the vehicle on the curvilinear-flat section, developing a necessary centripetal acceleration which is responsible for modifying the direction of the magnitude of the speed (V), and thus the vehicle transits the curvilinear-flat trajectory, thus:

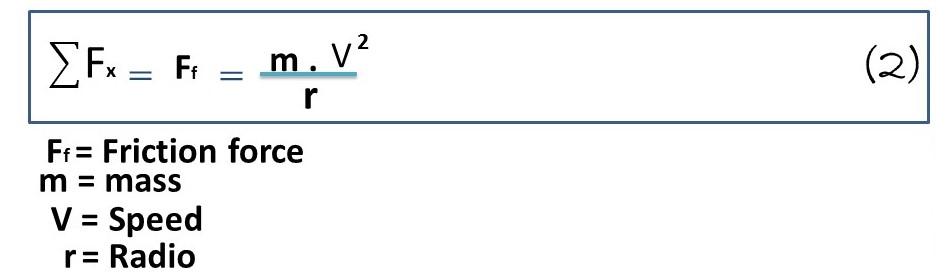
In this case, since we know the coefficient of friction (μ), we can use the following relation:

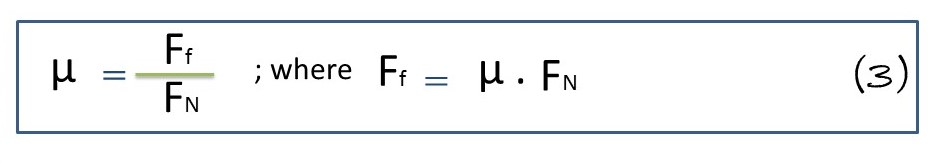
In this formula 3, we substitute the value of normal force (FN) represented by the formula 1, and friction force (Ff) represented by the formula 2:

Now all that remains is to clear speed.

Then we can calculate its value, and the same is the variable we want to find.

Thus, we were able to calculate the required speed, i.e., the maximum speed that the vehicle should have when traveling along the curvilinear-flat section without skidding, which is 7.34 m/s or 26.42 km/h (26.42 mph).

b.- To answer our second question, we will also analyze each of the axes linked to the vehicle's trajectory, but now adapted to the conditions of the curvilinear-inclined section:

Data:

V = 120 Km/h . 1.000 m/Km . h/3.600 s = 33,33 m/s. (Vehicle speed when passing the curvilinear-tilted section).

r = 105 m (Radius of curvature in the curvilinear-inclined section).

For these conditions we have that the forces that work in this axis are both the vertical component of the normal force and the gravitational force, highlighting also that there is no acceleration in this axis, so that:

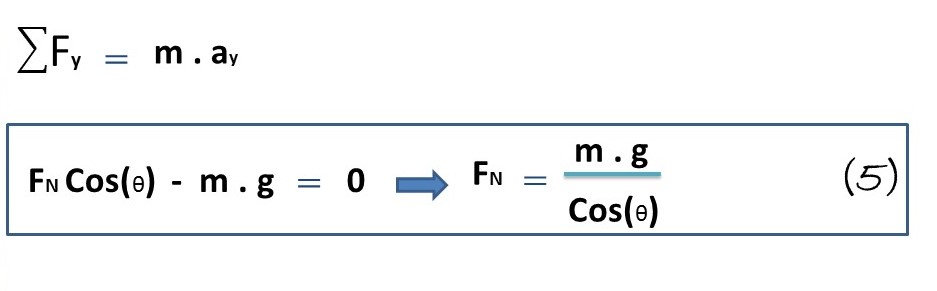
As for the x-axis we have.
For this case we have that the only force present is the horizontal component of the normal force (FN), in this axis the centripetal acceleration is developed, which manages to change the direction of the velocity magnitude so that the driver can keep the vehicle on the curvilinear-inclined trajectory, therefore, we have:

After analyzing both axes in relation to the above-mentioned section, we can substitute formula 5 in 6 as follows:

Thus, in order for the vehicle not to slide when passing through the curvilinear section indicated above at a speed of 120 km/h or 33.33 m/s, the inclination must be 47.20°.

Conclusion

Being able to drive on curvilinear stretches can be fascinating as long as the pilot has the experience and, in addition, the pilot must handle certain information about the road structure in order to avoid skidding on curvilinear stretches. This information can be obtained through the implementation of mathematical calculations or computerized programs through the use of technological equipment.

In this opportunity I wanted to show you how we can do it manually, which is fascinating to do and also awakens the interest of our students in applying any type of mathematical formulas, everything around us is interpreted by the algebraic language of mathematics and with which we have learned to know our wonderful environment.

In this opportunity we managed to know two important physical magnitudes as the maximum speed that should develop a car that intends to pass through a curvilinear-flat section whose radius of curvature is 22 m and a coefficient of friction (μ) of 0.25, and this speed turned out to be 7.34 m / s or 26, 42 km / h, but, we also calculated the angle of inclination of another section of a race where the vehicle transited at a speed of 120 km/h or 33.33 m/s, without skidding, giving as a result that the angle of inclination must be equal to 47.20°, since this angle would prevent the vehicle from sliding along the curvilinear section indicated above.

Until another opportunity my dear friends.

Note: The images were created by the author using Power Point, the animated gif was created using the PhotoScape application.

Recommended Bibliographic Reference

[1] Gravitational Forces. Link.

[2] Centripetal Force. Link.

[3] Newton’s Second Law. Link.