Greetings again my dear friends I hope you are all very well, everything that surrounds us we have managed to interpret thanks to the wonderful language of science, how much knowledge we get from any corner of the planet where we are, in our schools, high schools and universities, but in any other area of our lives where we decide to apply science in all its presentations.

This time we will analyze one of the movements that takes place around us as is the parabolic motion and, for this, again we will do it from the vision of a practical exercise that is possible to observe it to our environment, so then I share the following exercise to achieve the goal, ie, calculate various magnitudes of parabolic motion.

Exercise

In a beautiful golf course several players are making some practice shots in order to be able to determine the distance between the ball and the corresponding hole, these players are 75 meters away from the next hole, one of the players when making his shot gives the ball a velocity of 25 m/s, with a shot angle of the ball of 45°, this shot traces the trajectory of a parabolic motion from the moment the ball is shot until it reaches the ground, in relation to the above answer the following question:

a.- What is the distance reached by the golf ball?

Solution

Data:

V = 25 m/s (Speed of the golf ball when struck).
θ = 45° (Shot angle of the golf ball).
d = ? (Distance the golf ball travels).

a.- It is very important to visualize the projection of the path of the ball on each of the coordinate axes as shown in figure 1 below.

This image allows us to analyze this wonderful parabolic motion as two rectilinear motions according to their respective projection in each of the indicated coordinate axes, in addition it is also important to know the components of the initial velocity, therefore, in the following figure 2 we can visualize them.

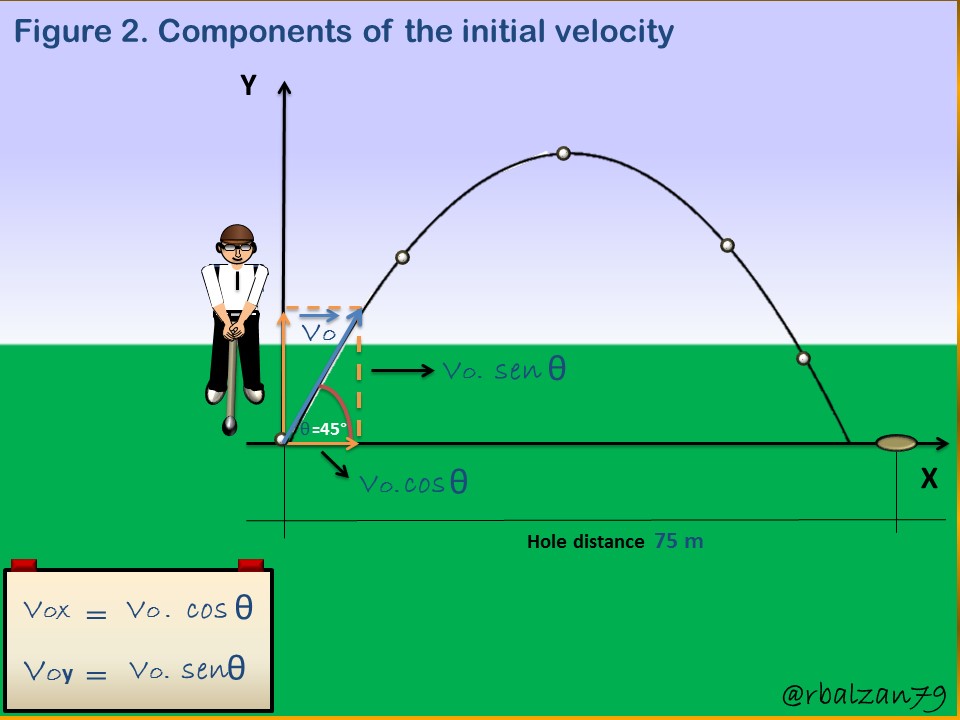
With the previous figure 2, we proceed to calculate the two components of the initial velocity in this parabolic launch, as follows.

With the value of each of the components of the initial velocity, we can now proceed to find the time of duration of the ball in the air, that is, the flight time (Tv), but first, we will find the rise time which when multiplied by two will give us the flight time, this will be done using the following formula 3.

In this way we have been able to find the rise time of the golf ball, therefore, the flight time must be twice this rise time, so we obtain the flight time as follows:

With the flight time we can calculate the range of the ball, i.e. the travel on the horizontal axis, so we can implement the following formula.

This was the distance (63.72 m) reached by the golf ball during the entire round in the air describing a parabolic trajectory impacting the ground 11.28 meters before the target hole.

Conclusion

Many are the physical phenomena that are developed in different activities of the human being among them sports in its different disciplines or modalities, the truth is that physical science and mathematics make excellent contributions in our lives and in any place where we are, this time we have been able to calculate several physical magnitudes in the development of a parabolic motion carried out by the trajectory of a golf ball.

In addition, it is interesting to highlight that it was possible to analyze this example through the composition of two uniform rectilinear movements, in each of the coordinate axes as indicated in the previous figure 1, it is the extraordinary thing about science that all its branches work together and, of course, generally for the welfare of all mankind or all living species on this planet, later we could analyze other interesting examples where physical science and mathematics will be present again.

Until another opportunity my dear friends.

Note: The images were created by the author using Power Point and Paint, the animated gif was created with PhotoScape.

Recommended Bibliographic References

[1] Rectilinear motion. Link.

[2] El movimiento rectilíneo. Link.

[3] Projectile Motion. Link.