Calculating the height of a mountain above sea level

Generally, we are on a flat surface at sea level or even below sea level, but at other times we may find ourselves at a height well above sea level, for example, on top of a mountainous formation and where atmospheric conditions vary in relation to pressure and temperature, these variables can help us to determine the height of the mountainous structure.
Exercise
A professional hiker decides to climb to the top of a mountain that borders the sea, it is his passion to be able to feel the air currents at such a high altitude and, in addition, it is his job to determine the altitude of each of the mountain structures he decides to conquer, When he is at the top of the mountain he tells his teammate that he is at the lowest part of the mountain, that the pressure at that altitude is 534 mm of Hg (millimeters of mercury) and that the air density is 1.75 g/liter, noting that the pressure at sea level is 760 mm of Hg, then, answer the following question:
a.- What would be the height of the mountain above sea level?
Solución
Data:
P1 = 760 mm de Hg (Sea level pressure).
P2 = 534 mm de Hg (Pressure at the top of the mountain).
d = 1,75 g/ liter (Air density).
g = 9,8 m/s2 (Gravity acceleration).
h = ? (Mountain height).
a.- Before starting to solve our question, it is very important to emphasize that all fluids (liquid and gaseous), will exert a certain pressure on the walls of any container containing them and also on those bodies that are within the action of these fluids, this force or pressure will always act perpendicular to these surfaces analyzed, therefore, the pressure (P) exerted by a certain fluid of density (d) on any point located at a certain depth (h) of the surface, will be numerically similar to that pressure exerted by a certain column of fluid of height (h), these variables are not provided by the fundamental theorem of hydrostatics by means of the following algebraic formulation:

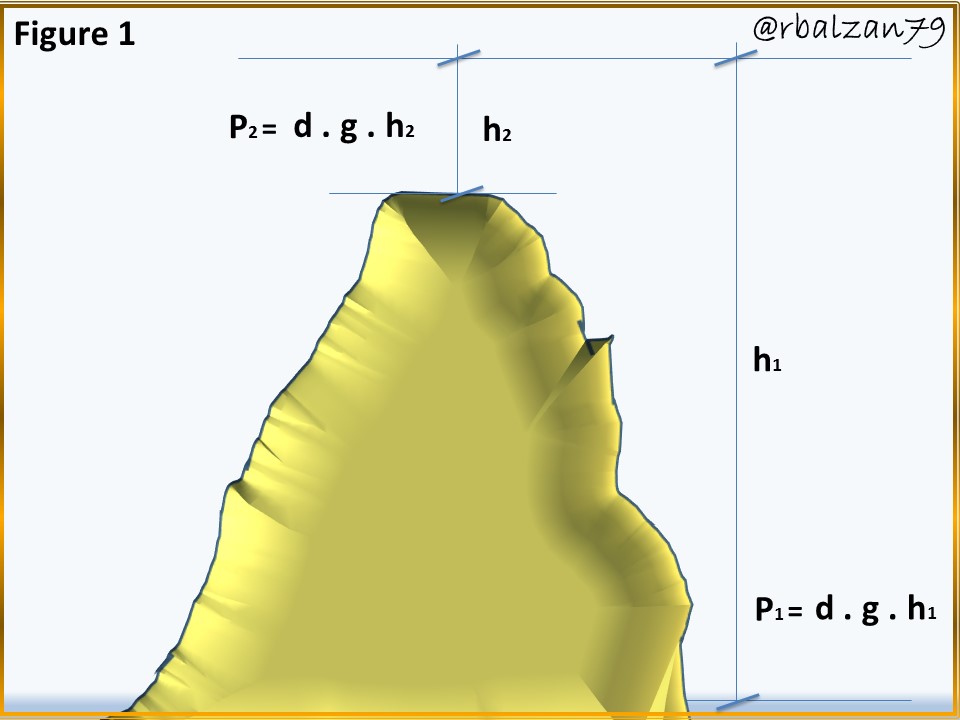
Thus, as we wish to calculate the height of the mountain formation in Figure 1, then:

Therefore, we apply the fundamental theorem of hydrostatics at sea level and, also at the height of the mountain where the hiker arrives, then, looking at figure 1, we can determine:
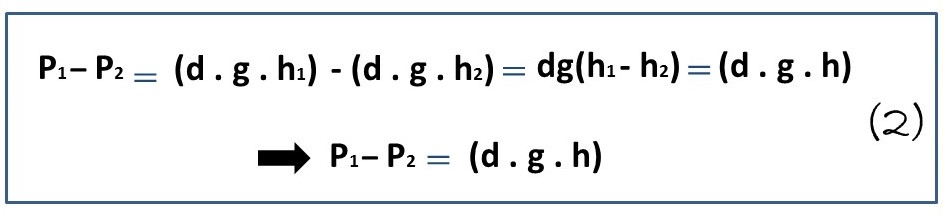
Then from formula 2, we clear our requested unknown, i.e., height (h), therefore, we have:
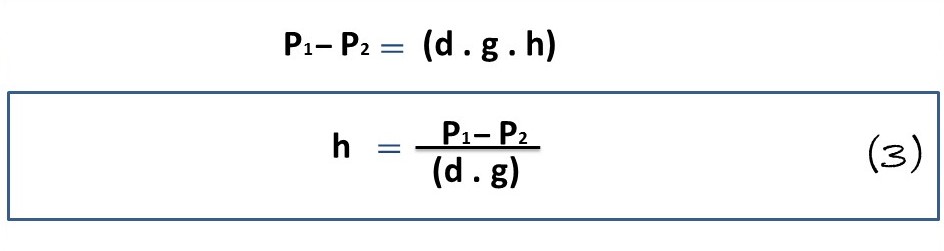
Therefore:

Now we transform the density of the air in this space into units of the international system:
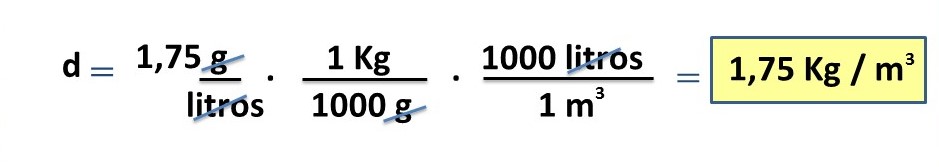
In this way we proceed to substitute the values in the formula 2 and, in this way, find the requested height.
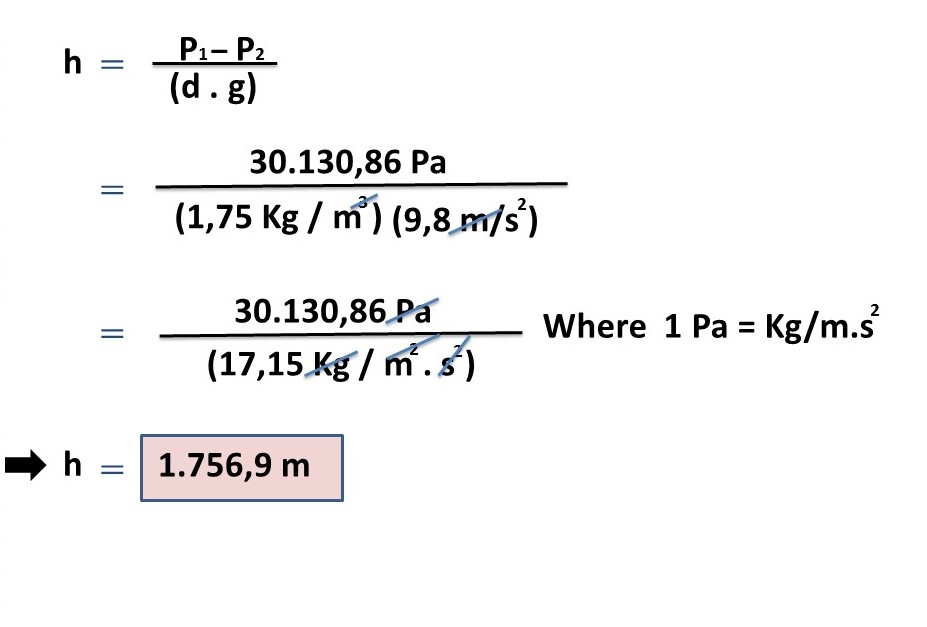
We were able to find the height of the mountain where the professional hiker climbed to the top, therefore, he managed to climb to a height of 1,756.9 m.
Conclusion
Many of us undoubtedly hear at every moment the reference of the sea level and, this in order to search or find or establish some kind of height of a certain location or mountain structures, among others, the truth is that with some data, it is possible to know the altitude of the above mentioned examples, as we noticed in the development of our exercise, where, through the implementation of some mathematical formulations we managed to know the height of a particular mountain.
It is always important to know that we can apply these mathematical formulations and make them very practical at the time of explaining any event that is around us, in this way we continue to verify that everything around us is expressed through the language of mathematics and physical science, moreover, are at our disposal, later we will continue to know other important examples where we can know some essential physical variables through any type of mathematical formulation.
Until another opportunity my dear friends.
Note: The image was created by the author using Power Point and Paint.
Recommended bibliographic references
[1] Hydrostatics. Link.
[2] Hydrostatic Pressure. Link..
Physics calculations is always interesting. Just that most time people always find it difficult
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Mountains above sea level have long been revered as symbols of strength, spirituality, and mystery. In taoism beliefs these towering natural structures are often seen as sacred, representing the harmony between heaven and earth. The higher the mountain, the closer it is to the divine, offering a pathway to spiritual enlightenment. Taoist monks and practitioners frequently seek solitude in these elevated terrains, meditating and seeking wisdom. The idea of ascension in Taoism aligns with the concept of personal growth, emphasizing the importance of balance and connection with nature. Mountains above sea level, therefore, embody both physical and metaphysical significance.
Posted using STEMGeeks