Modelling the World Numerically
Solving partial differential equations (PDEs) analytically is not always straightforward. In fact, in many cases, it might be that an equation system is not solvable at all. At least not analytically.
And that's where numerical methods come into play. These methods allow us to solve complex PDEs efficiently using computers. Here, the goal is not to find a concise analytic expression that describes the solution to our problem. Instead, the goal is to find the solution values at discrete points within the problem domain.
To solve PDEs there are many different numerical methods. Well-known methods are the Finite Volume Method (FVM) and Finite Element Method (FEM).
 Numerical simulation of the flow around a wind turbine. Source: my master's thesis
Numerical simulation of the flow around a wind turbine. Source: my master's thesis
While these methods differ from each other, both reduce the continuous PDE into a system of linear equations (i.e., a finite discrete problem). It is these kinds of systems that computers can solve fast and efficiently. Generally speaking, such systems look as follows:
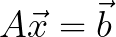
where A is the system matrix b is a right-hand side vector and the unknown solution to our problem is given by x. Hence, to solve such a system, the inverse of A needs to be computed. This yields:
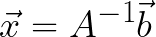
The downside of the above is that computing an inverse of large matrices can be very computationally intensive. That is, your computer will need a long time to compute it. Luckily, over the years, scientists came up with many different tricks to obtain or to approximate the solution to our system faster.
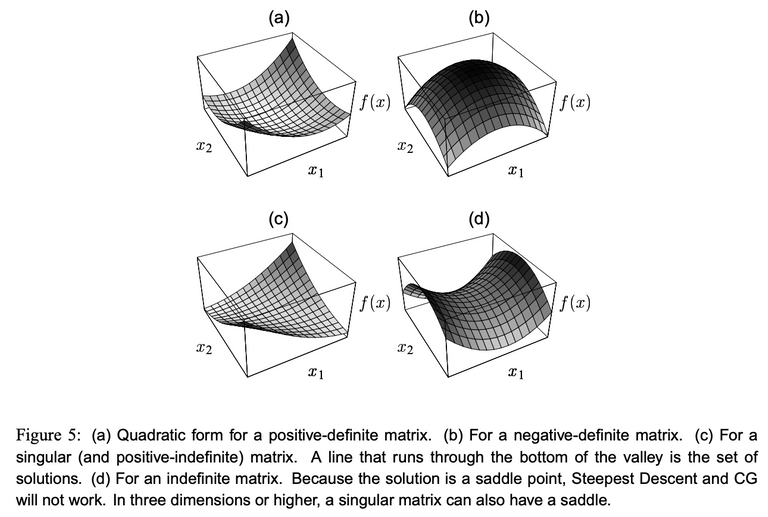
A very basic approach to solving a large linear system is the conjugate gradient (GC) method. This method is able to solve linear systems for which the system matrix A is positive-definite. This sounds complicated, but simply put this is the case when A is symmetric and has positive eigenvalues.
The idea of GC is to rewrite the equation in quadratic form and minimize x on this equation:
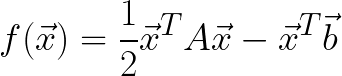
The system of equations can be written in this quadratic form with a minimum due to the requirement of positive-definiteness of A. E.g. when A is indefinite, the quadratic of the system yields a saddle point problem that doesn't have a minimum. This for example is the case for the PDE that defines the Navier-Stokes equations used to describe fluid flow problems.
Hence, when solving PDEs using numerical methods, it is key to know the characteristics of the equation system you are solving. For the saddle point problem, for example, other methods such as the Generalized Minimum Residual (GMRES) can be used instead.
A very detailed and comprehensive work on the CG method can be found here. Other than most works, this document succeeds in explaining the topic in layman's terms.
Yay! 🤗
Your content has been boosted with Ecency Points, by @michelmake.
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more