When a circle in-scribes a trapezium
Hello math bugs(🐞) and hivers(🐝)
I hope you had a good weekend.
I have come up with another cute one. The problem today is when a circle is inscribed a circle, you have to find out its radius when a non-parallel side is given. You may think, " No! there no side given, actually two portions of two sides given only!!"Actually if you check properly you will find the given side is hidden a bit.
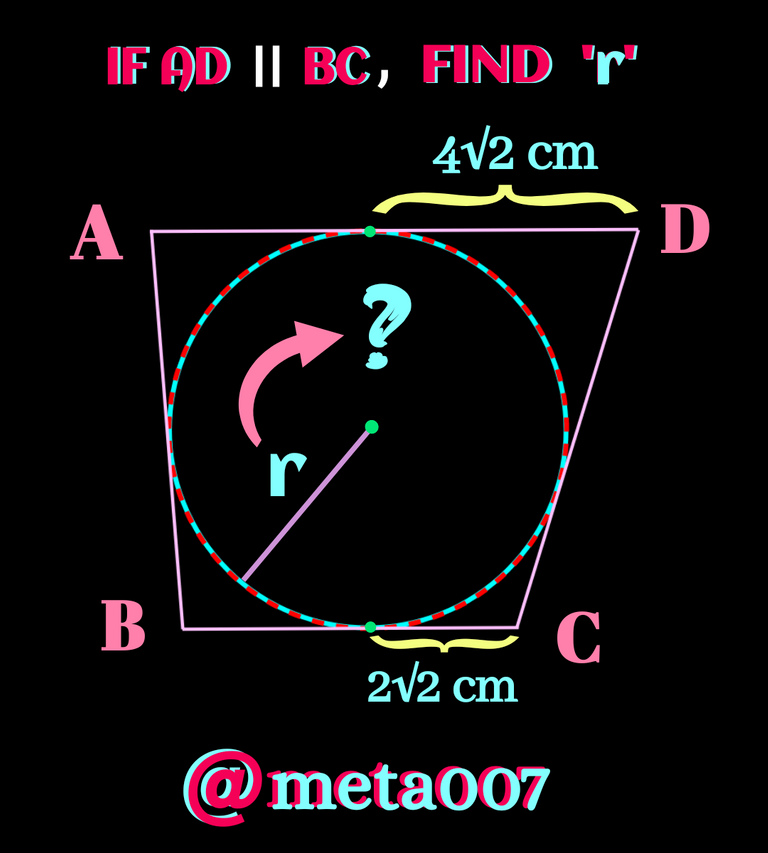
Now if you find the side, give it a try first.Find the radius(r).
Okay, before heading towards solution, I just want to remind you some concepts/postulates/axioms first. Here we go:
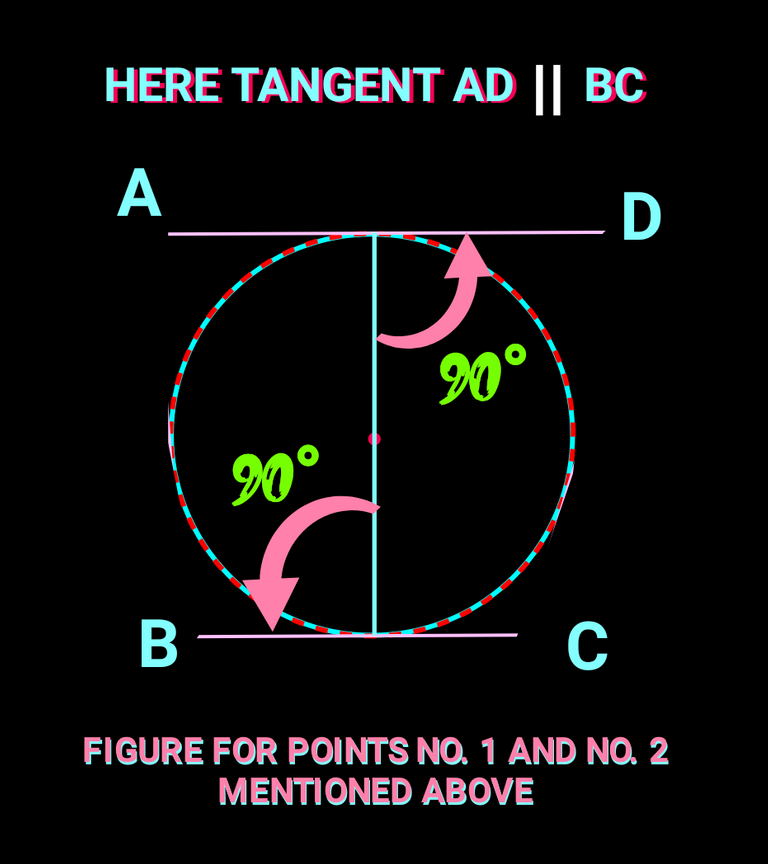
✅(1) The distance between two parallel tangents of a circle always passed through the centre.Thus the distance becomes its diameter.
✅(2) The radius of a circle is always perpendicular to its tangent. Hence, in the problem, the diameter is perpendicular to both of the tangents. Check the following figure:
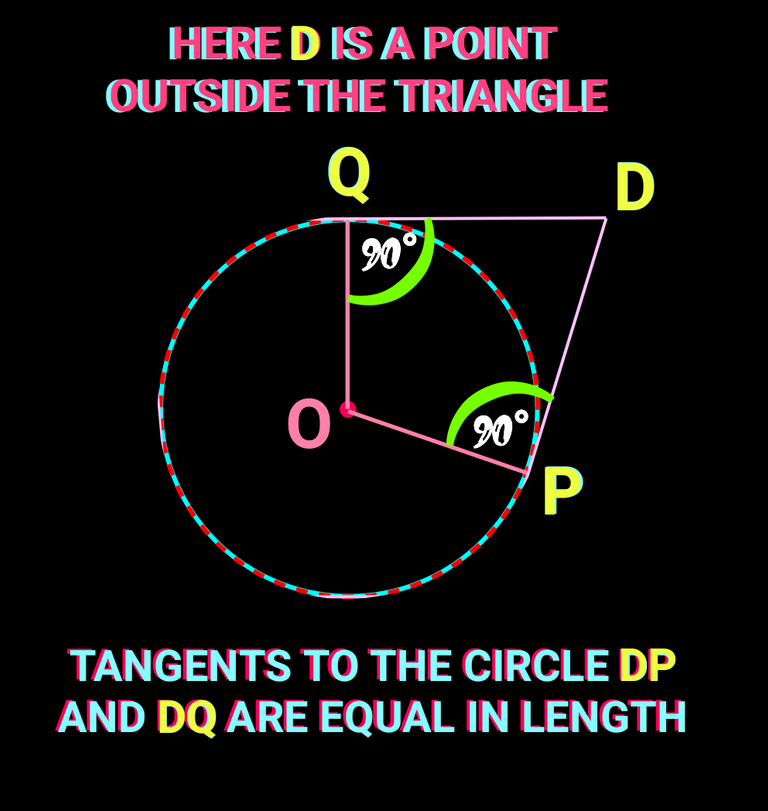
✅(3) Two tangents of a circle from a particular point outside cover equal distance to the point of contact.Check the following figure:
The same way the following figure is made:
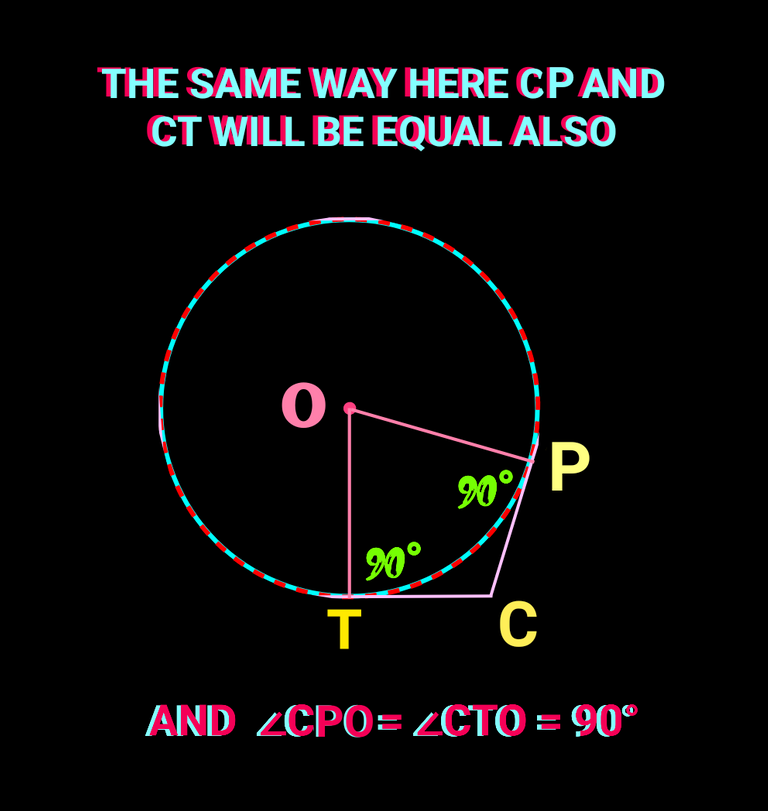
✅(4) Conditions of similarity of right angle triangles.And then need to find out thr relation between sides using it.If we combine the previous two figure we can find a right angle triangle.we just need to connect CO and DO. Check it below:
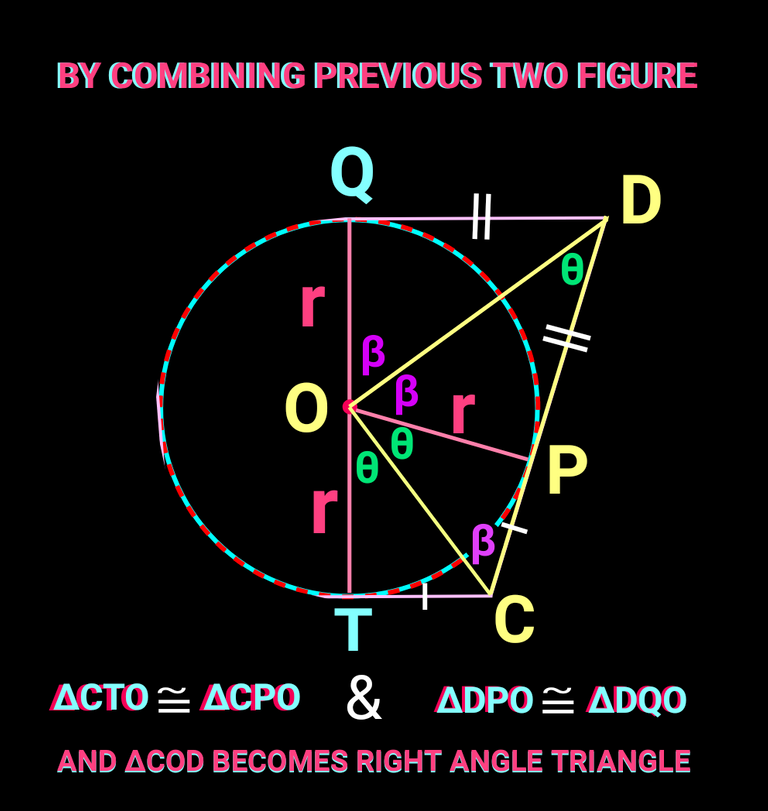
If you haven't figure out the answer yet, try it now ;you have all the concepts you need to solve it. And if you still don't get it, no worry ,let me now do it step by step.
You may be aware about similarity very well and if not check my previous detailed post on similarity.
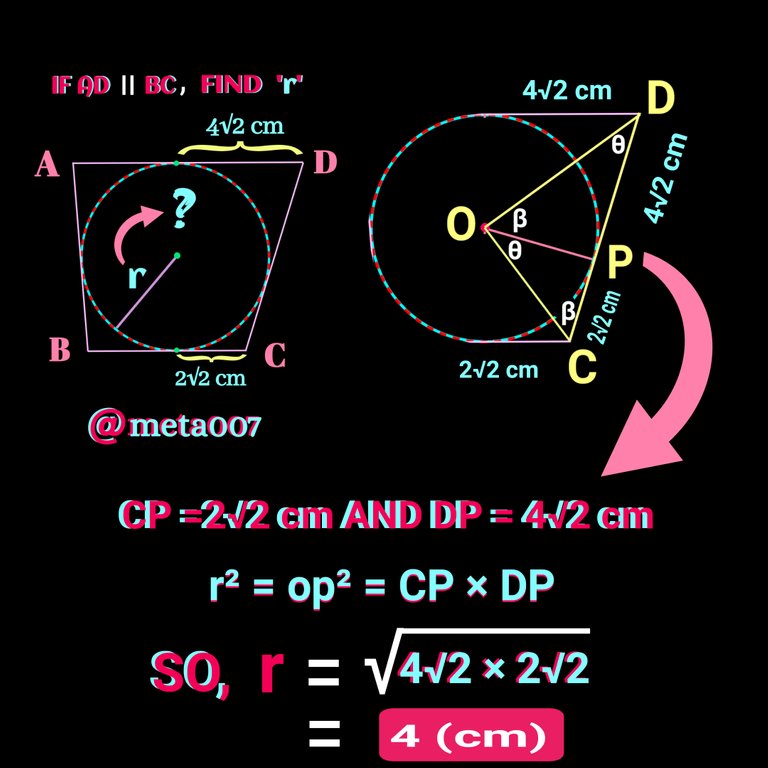
Let's consider the right angle ∆COD only. Using similarity we can write OP² = CP ×DP. How!! Check the following figure:

So, the required answer is "r" = square root of (4√2 ×2√2) cm.That is "r" = 4 cm 😃. Check the figure also:
All the figures made by me using Android apps. There may be some mistake while typing or making figures, please excuse me for that.
Thank you so much friends for stoping by. I hope you enjoyed it. Have a good day.
All is well
Regards: @meta007
You are really doing a marvelous work here in hive and I pray you get the great recognition you deserve.
What an elaborate step by step explanation to drive this home.
Indeed, it was great to come across this blog
I am glad that you took time to go through my work. Thank for your kind words ,wish and visit.
You're always welcomed man
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
Thanks for including @stemsocial as a beneficiary, which gives you stronger support.
Congratulations @meta007! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 20000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts:
Support the HiveBuzz project. Vote for our proposal!
Thanks for the back to school math refresher 😜 !PIZZA !KING
Well done King @meta007, blitzzzz(7/13) is appreciative of the time and attention you put into writing this post. Your efforts are truly valued.
Creating quality content has paid off! @blitzzzz has sent you 0.025 HKGENTHREE as a thank you for your efforts.
BTW! You will find powerful and charismatic NFTs in the AVATAR PACKS that you can use in all our games.
PIZZA Holders sent $PIZZA tips in this post's comments:
@blitzzzz(10/20) tipped @meta007 (x1)
Please vote for pizza.witness!