How To check if denominator divides neumerator.
Hello math bugs(🐞) and hivers(🐝)
I hope you are strong and stout and doing good in life.
Today I am going to share you some important facts about divisibility.The word divisibility itself is very interesting.Do you know why? Every consonant in the word follows a vowel and the vowel we use is the same 'I' and even 'y' is a semi-vowel.Thus we got 5 'I's in the word divisibility.I don't know any word having same five vowels ..lol. it's pronunciation is also amusing ; di-vi-si-bi-li-ti(y).

Some people crams multiple tabel upto 20 and some do more. so checking divisibility is easier for them if they know how to find factor of a large number but for that they also need to know concept behind factorisation.If the NEUMERATOR and the DENOMINATOR are a composite number , we can easily factor the them to make calculation easier but when it comes to a prime number sometime with got stuck.
I too myself never cram multiple tables. When I was younger , I was asked to cram them but I was actually never good at cramming things and I still lack it.Rrapeated practise helped me to learn some basic lower tables.😂😂
I'll suggest you to make it to the end cause everyone knows the rules for lower numbers but as I talking about divisibility, I should start from the begining.Without further ado let's get to the topic:
DIVISIBILITY:
✅ BY ZERO (0):
If we wanna divide any number by zero, It won't make any sense as for now. Zero multiplied by any number gives you a zero also. Zero multiplied by a number in infinity produces a zero aslo.If we devide a number by zero, we can't say answer is infinite.The best answer will be NOT DEFINED.Why it is so , checky it below: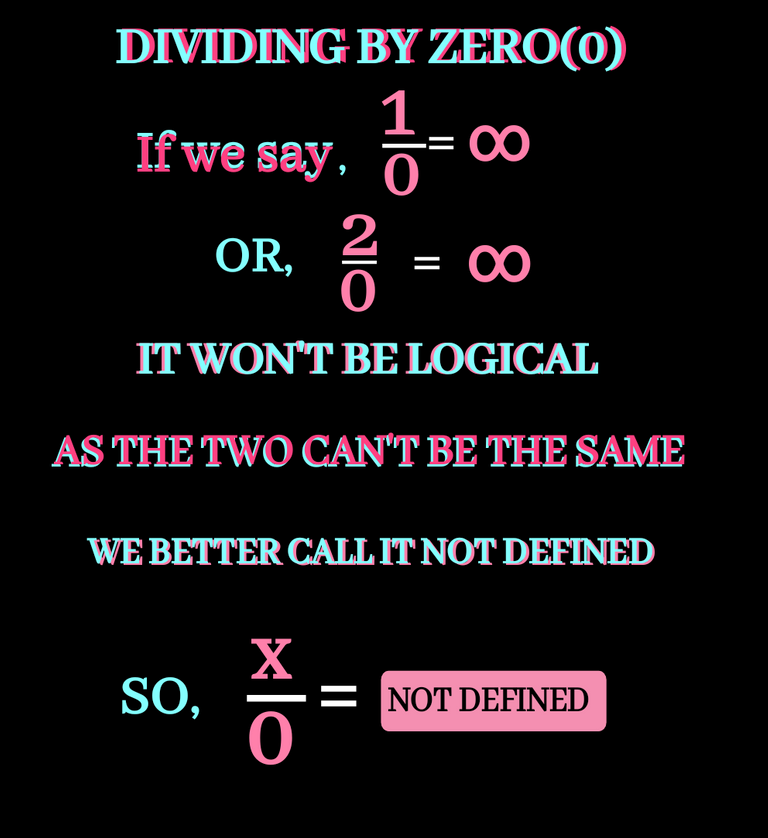
✅ BY ONE (1):
This is the simplest one. If we divide any number by one (1) ,the answer is always the NEUMERATOR. I think there is no need of any example.Still I decided to take an example at least for each of them as below:
✅ BY TWO (2):
If it is an even number, it is always perfectly divisible by two (2). Also we can say if a number ends (Unit digit) with multiple of two, it is always an even number and must be divisible by two (2). let's check it below:
✅ BY THREE (3):
If sum of digit (SOD) of a number is three, the number is perfectly divisible by three (3). As example , take random number ; let's say 9756. I can clearly see it is perfectly divisible by 3. Cause SOD of 9765 is a multiple of three or can say is divisible by 3.
Note: When we find SOD of a big number, adding all digit can be annoying or time consuming, instead we can remove 9s from the number because it won't affect the SOD. The 9(s) we gonna remove or ignore, in this regard, can be a single digit or sum of more digits
If sum of digits (SOD) comes as more than one digit, we can find SOD of the SOD. The process can be continued till we find a single digit SOD.
Let's check the following figure:

✅ BY FOUR (4):
When final two digits of a number is divisible by four (4) , the number will also be completely divisible by it. More precisely If the number made by digits at tens place and ones place of a number is divisible by four (4), the entire number will also be completely divisible by four (4).Check details below:

✅ BY FIVE (5):
If unit digit of a number is zero (0) or five (5), the number is divisible by five(5). Or we can say if a number end with zero(0) or five(5), the number is divisible by five(5). Also check the figure below:

✅ BY SIX (6):
Divisibility concepts of two (2) and three (3) have already been discussed. As six (6) is multiple of two (2) and three (3), If a number is divisible by both of the factors (2 & 3), the number will also divisible by six(6).
✅ BY SEVEN (7):
This is a special case. Let me tell how we can check if a huge number is divisible by seven (7) or not. We have to separate the digit in unit place. Then we should multiply it by two (2) and then the product should be subtracted from the remaining part of the original number.If answer after substracting is divisible by seven (7) , the original number will also be divisible by seven (7). Check detail below:

The process shown above can be used multiple times until we find us comfortable if the subtraction is divisible by seven or not.Detail is at the bottom of this post.
✅ BY EIGHT (8):
The Rule is similiar to the divisibility rule of four (4). In case of four(4) we checked the last two digit.If number made by last two digit of a number is divisible by four(4), the original number is divisible by four(4).In case of 8 we have to do the same but here we should take last three digits. Check it below how:

A number having three zero (0) in the end is always divisible by 8. We have to check just last three digits.
✅ BY NINE (9):
This one is similiar to divisibility rule of three (3).Here we have to find sum of digit (SOD).If SOD is divisible by 9 , the number will also be divisible by 9 also. Or we can say the SOD must be a multiple of nine (9). Here we can do the same as we do for three(3). To find SOD , we need to add up the all digits.We can remove 9s or the digits which add up to make a 9. After removing all the 9s, the SOD of remaining digits will SOD in this regard. Another point is while removing 9s if there is no digit left that means the original number must be divisible by 9. Also check divisibility rule for three (3) if you are confused.
✅ BY TEN (10):
The easiest one comes now. If a number end with a zero(0), the is divisible by then (10). Cause Zero (0) in neumerator and the zero(0) in denominator get cancelled.😀
✅ BY ELEVEN (11):
This one is also special case. For eleven (11) , we have to find SOD of digits at odd place and even place separately. Then we have to subtract the two SODs. If the result is divisible by 11, the original number will also be divisible by 11 or we can say the subtraction of two SOD mentioned above must be a multiple of 11 if the number is divisible by eleven (11). Check details:

✅ BY TWELVE (12):
Twelve is multiple of 2,4,6. If the number is divisible by both three(3) and four(4), it will also be divisible by 12.
But the problem comes when it is a prime number with two, three digits.I am gonna show you how we can find divisibility rule for any numbers specially for prime numbers.
Most people are know to divisibility concepts of lower numbers as I have discussed above.Now It's time for advance approach.
HOW TO MAKE DIVISIBILITY RULE:
You must have seen the concept of divisibility for number seven (7).If we want to check if a number is divisible by 7 or not, we separate digit in unit place of the number and then we multiply it by minus two (-2).Then we add the negetive product to the remaining part of the number and if the final result is divisible by 7, we know the original number will a multiple of 7 and hence it will be divisible by 7. If after adding the negetive product of unit digit and -2 to the remaining part, be still a large number , we can do the same process again again until we get a lower number which comes in lower multiple table.I have discussed this above in divisibility by 7.
Now the question arises what is this minus two (-2)? Where does it come from? It is the odd factor. Let me show how do we find it and what is it's importance.
Now here am going to share you how can be divisibility rule of 13 and then I'll explaine the above context. Totient method

Let's check how this odd factor is useful:

Let's draw the conclusion :

I hope you find this article valuable.
Thank you so much for stoping by.
Have a great day
All is well
Regards: @meta007
Greetings and thanks for sharing, this topic is good to share
Thanks man for appreciating and visiting.
This post has been manually curated by @bhattg from Indiaunited community. Join us on our Discord Server.
Do you know that you can earn a passive income by delegating to @indiaunited. We share 100 % of the curation rewards with the delegators.
Here are some handy links for delegations: 100HP, 250HP, 500HP, 1000HP.
Read our latest announcement post to get more information.
Please contribute to the community by upvoting this comment and posts made by @indiaunited.
Yay! 🤗
Your content has been boosted with Ecency Points, by @meta007.
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more
Really impressive how you take the time to break these maths down, must be alot of work. Well done🔥
Thanks for the appreciation queenstarr.
Yeah it takes huge time to make those visuals and the math part is easy for me.😀
You are so kind... Thanks for gifting 450 ecency points.
I have seen people to send many greetings through on chain emojis but I have none but What I can is to send some💖💖🙏.
Awe! No worries, well deserved. Keep up the hardwork🔥🥂
I never knew this secret! If I knew this secret when I was still at school, maybe I would like a guru 😂
The divisible by 7 was difficult that I had to read it again. I just hope I would be able to remember all of this.
Easiest would always be the 0, 1, 2, 5 and 10.
Yeah checking divisibility by 7 is quite different from the others and it is not taught in school.
if you check bottom three frame of my post,it will be cleared with the help of a little concentration.
I am really surprised to hear the word 'guru' from you.How do you know it?
You are are really guru at making good blogs and for maths ,You can still be a guru if you have enough interest in it.😀
I tried to re-read it again with concentration so I was able to understand it. It's just a bit tricky and hard to remember because it's kinda different from the rest.
Maybe from watching tv shows or movies? Hahaha I'm not sure!
I think you are a Math guru, @meta007! And you are making us learn from what you know.