Hello math bugs(🐞) and hivers(🐝)
I hope you are strong and stout & doing great.
Here , I have come up with another cute and interesting problem based on two different squares. Side of two square given and you have to find out the area of the triangle shaded yellow as you can see in the figure given below.
From the figure , we can easily find out the lenght of the line segment BZ easily using pythagorean triplet or theorem. So, We know the value of BZ. So, now the required area can be found easily and which is equal to (1/2 ×AZ ×BZ)=30 cm².
Check Pythagorean TRIPLET short cut with full details.
But if you are aksed to find the area of the other triangle placed above it, it may trouble you if you are facing it for the first time. So, My today's work will be on it. Thumbnail was little bit different because I wanted lure people a little bit giving an easy one.🤣🤣
The question can be formed as If ABCD and AXYZ are two squares , area of ∆ABZ = 30 cm and AZ = 12 cm then find area of ∆PBY. Check the follwiing figure.
After finding BZ frim pythagorean triplet, we can find BY which is (YZ - BZ)= (12- 5) cm= 7 cm. Now notice carfully if we find PY, the job is done because we then will have base (PY) and Height (BY) of the right angle ∆PBY.
We should keep it in mind that the ∆ PBY and ∆ BAZ are similiar. How!!! let check the following figure.
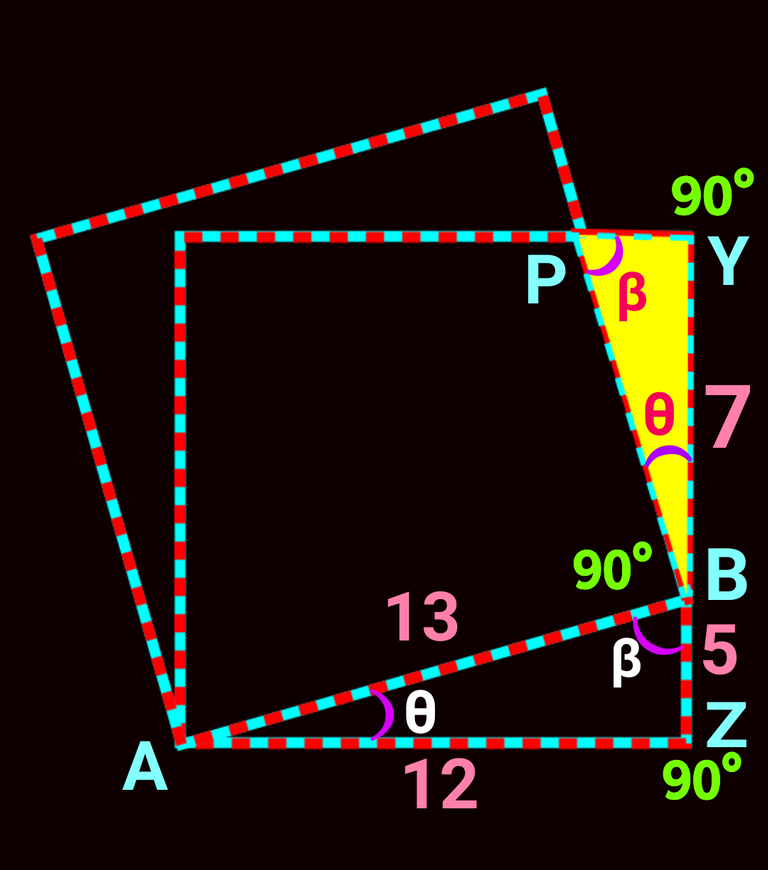
Here sum of every θ and β is 90°. The straight ∠YBZ=(θ+ 90°+β) = 180°. Hence (θ+β)= 90°. In case of both of the triangles (θ+β) is also 90°. Now using similarity we can write the following expression:
PY/BZ = BY/AZ
Or, PY/5 = 7/12
Or, PY = 5×7/12
Or, PY = 35/12 [cm]
How !! Check details of Similarity
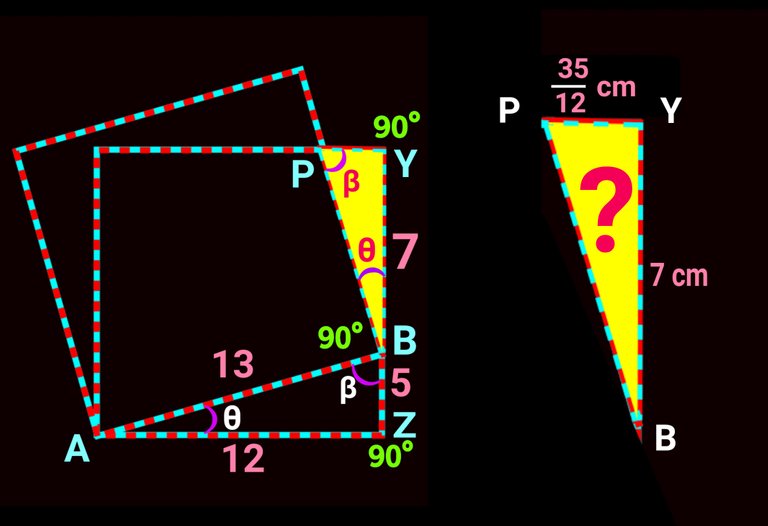
Now the area of the ∆PBY is given by as follows:
∆ = 1/2× BASE × HEIGHT unit²
= 0.5 × PY × BY unit²
= 0.5 × 35/12 × 7 cm²
= 25 × 49 / 120 cm²
= 25 × (50-1) /120 cm²
= 1225 / 120 cm²
= 102.08 /10 cm²
= 10.21 cm² (approx)
No calculator is used. If you wanna learn oral calculation, please hit a comment below. I will be glad to reply.
Please try to ingnore the silly mistake(s) if there is any.
All the images(figure) are made by my using android apps.
I hope you like my today's work.
Thanks you so much for your patiently visit.
Have a great day
All is well
Regards: @meta007
