Research diaries #9: types of convergence
A sequence is a list of ordered points. As we progress through a sequence it could be that these points are approximating some point. For example, look at the graph below
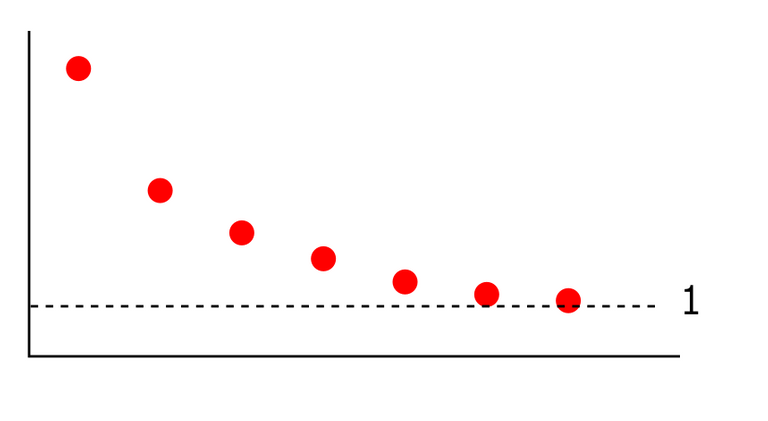
On the x-axis the position of the point in the sequence and on the y-axis the value at that position
We imagine now that this sequence is infinitely long, meaning that there are countably infinite points in this sequence. We investigate this sequence as lying on the real linea. The sequence very clearly approximates 1. However, 1 is not contained in this sequence. Denoting xn by the n-th point in the sequence. We suppose that xn = 1+ 1/n. The distance between 1 and xn becomes smaller as n increases. Or more specifically, for any y>0 there exists an n such that |xn-1|<y

The distance |xn-1|, indicated by the dotted line, goes to zero as n goes to infinity
Perhaps you might have seen this differently treated in your calculus class. The underlying space you were working in is then probably an Euclidean space, so Rn, with the natural distance. But the above connects to a more general treament of sequences, namely sequences in the context of metric spaces which are spaces with a general distance function.
Perhaps we could look at convergence differently. We could look at the distances of consecutive points so |xn- xm| and see if this gets smaller. More specifically, for all y>0 does there exist N such that for all n,m >N we have that |xn- xm|<y. This type of covergence is called cauchy-convergence. We will refer to the convergence from the first example just as convergence. It is not too difficult to see that our earlier example also satisfies this. An example of a sequence which does not cauchy converge:
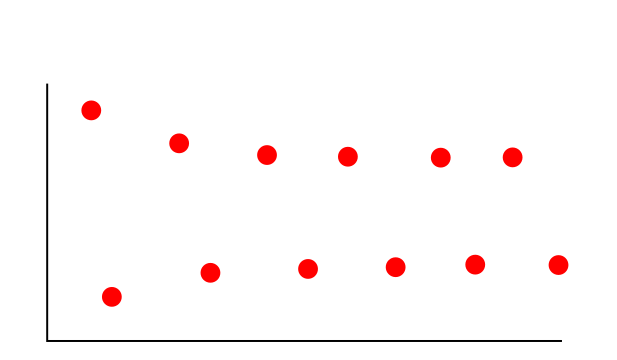
The distance between the odd and even indexed points does not become arbitrarily small for sufficiently large index value
But clearly the above sequence also does not converge. It can be shown that a convergent sequence is cauchy (see for example Theorem 6.8.2 in this metric space book) but not the other way around. Let's skip the proof of the former and look at a the latter. We return to our first example. Suppose that we investigate the sequence as lying on the real line with the number 1 removed. Then, the distance between the sequence and the limit cannot be measured because the limit is not contained. However, we can still consider the cauchy convergence because we are measuring the distance between points, additionally, this distance can become arbitrarily small.
Although it is not generally true that cauchy convergence implies convergence we can restrict to spaces where this implication holds. These resulting spaces with specialized distance functions are of great importance in math. These are Banach spaces. A plethora of math can be done on these spaces. It forms one of the cornerstones in modern math.
That's all for now hope you enjoy this little exploration into the fundamentals of modern analysis.
Cat tax

Yoyo analyzing birds
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Congratulations @mathowl! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 35000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Hmmm, infinitesimal calculus.
I would have loved if you had added vertical in brackets following the dotted lines in your second diagram to avoid confusion. In my eyes originally, your dotted lines also appeared as small dashed lines. So i was seeing dotted lines (relatively) everywhere and wondering the one you were referring to, until i made sense of it with the math.
Nice piece of writing though.
Nice seeing you here
That is a good point. I will keep it in mind for a next analysis post ^^