Research diaries #8: Weakening differentiability
In high school we all learned about how to compute the derivative. Here we will look at what it means for a function to be differentiable and how to weaken it.
A derivative of a function at a point gives the slope of the tangent at that point. See the pretty figure below.
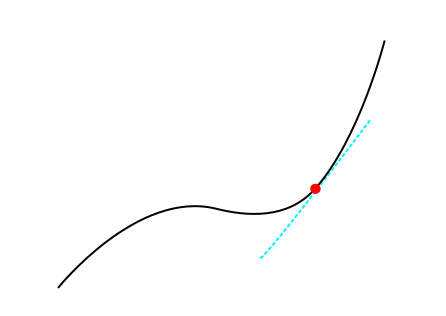
The blue line we can express as ax+b where a,b are two constants determined by making the line tangent to the black curve. The derivative is given by a
To make it more applied you can think of this graph as a function of position and time. The derivative at a give time then correspond to the speed at that time. Is a derivative always well-defined? No, Let's give an example:
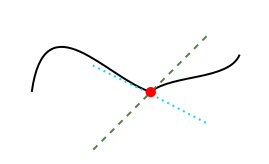
The black curve is dented. It has a sharp point at the red spot. If we do the previous procedure to find the derivative the derivative could have 2 different values
We see that at the point we want to compute the derivative we could draw 2 different lines that are tangent in two different ways: one approaches from the left and the other approaches from the right. So the derivative is not well defined because the slope can have 2 different values. We call this function not smooth. However, these 2 lines still give us information about how steep the function is. This weaker type differentiability is called Lipschitz continuity. I will skip the mathematical formalities and you can keep your intuitive understanding.
So what do functions look like that are not Lipschitz continuous. A simple example is

A discontinuous curve
The disconintuity makes it so that I cannot draw this double cone shape as before.
In the domain of mathematical analysis there is a large field which considers weak versions of properties we considered in a basic calculus course. By weakening these properties we can somehow obtain better results because the conditions are not that severe. Specifically, in the field of differential equations this is a common approach to find solutions of complicated equations which only exist in some weak sense. Maybe that is a nice topic for a future post.
All images made by me ^^
Cat tax

research dat !BEER
Thank you for your witness vote!
Have a !BEER on me!
To Opt-Out of my witness beer program just comment STOP below
Thanks for the beer, cheers :D
Thank you for your witness vote!
Have a !BEER on me!
To Opt-Out of my witness beer program just comment STOP below
View or trade
BEER.Hey @mathowl, here is a little bit of
BEERfrom @bluerobo for you. Enjoy it!Learn how to earn FREE BEER each day by staking your
BEER.Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.