Research diaries #7: Regular versus chaotic motion

This post connects to one of my old post on chaos in the logistic map. Here we will be looking at the sine circle map and showing how a critical feature of the map determines when chaos can occur

The sine circle map is a more complicated 1-dimensional map compared to the logistic map. The exact form is not that important for this post. As with the logistic map, the sine circle map depends on parameter(s) which when varied wil change the long time behaviour of the motion generated by the map. The sine circle map has 2 parameters whereas the logisitic map actually has one. But we will just fix one of these parameters and see what the long time behaviour looks like.

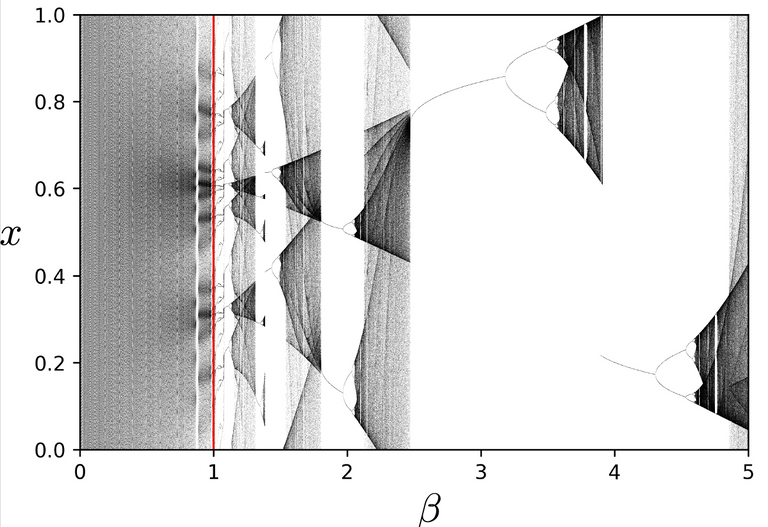
For the experts beta=K in the definition over here and Omega = 0.606661

After the red line it looks like the logistic map's long time behaviour. Let's repeat the corresponding plot over here:

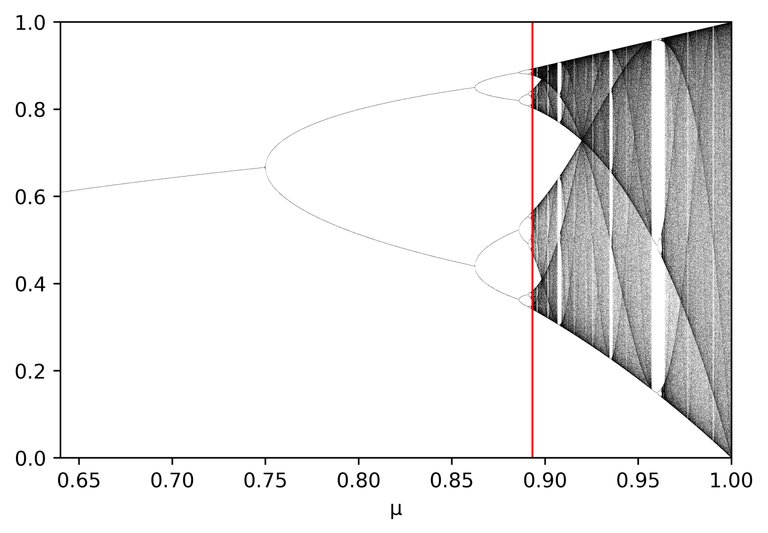
In red the transition to chaos. This is not related to the red line from the first figure.

So why does this chaotic structure not occur for beta<1 in the first figure? Chaos is caused by a stretching and folding dynamics over the motion in the one dimensional x-space. Folding means that if you take a short interval in the x-space this is folded double under application of the map. However an interesting property for beta<1 is that the maps are all invertible. This means that that motion backwards in time is also deterministic. Observe that the folding property does not implies this backwards determinism since for example, if you fold a piece of paper the resulting two paper sides map to a single location on the paper.

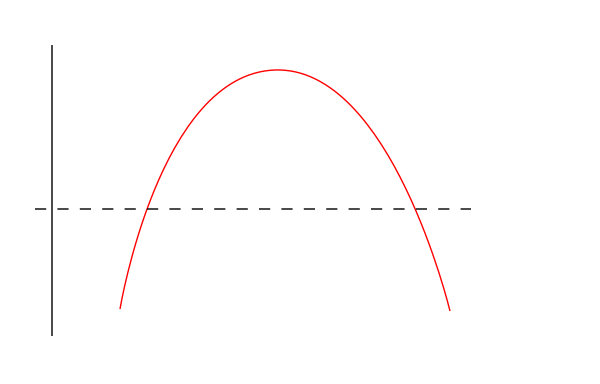
Folding is not invertible

A very nice book which treats interesting dynamics associated to the sine circle map is Chaos and nonlinear dynamics: an introduction for scientists and engineers by Robert C Hilborn et al. It is well suited for peeps not initiated to scary math. It also contains some elementary proofs including the invertibility property.

The sine circle map is in the literature commonly used as an example of phase locking or arnold tongues. The is a phenomenon where there are at least two interacting frequences which are locked to each other. This will be a topic for another post. But you should absolutely check the pretty pictures in the wiki.