Research diaries #14: An optimization puzzle
Occasionally I do some algorithm puzzles. This is quite a fun one from Hackerrank with rubik like features.

Today starting with the cat tax ^^
Suppose we have an array with integer entries. This array is of size 2n with n being an integer. Let's call the array A. We are allowed to perform 2 types of operations on this array:
- column flip: reverse the order of all entries in a single column
- row flip: reverse the order of all entries in a single row
The main question is: Applying these two flips any number of times to A what is the maximal value of the sum over the elements in the left top n by n sub-array.
Let's first have a look at a simple example.
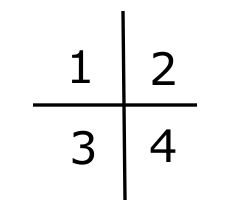
It is a 2 by 2 matrix. So the goal is to move the right bottom corner element to the left top element. Applying a column flip to the right column and then a row flip to the top row we are done.
That one was simple. But things get already a bit more difficult if the matrix is a size large 4 by 4. You can give that a try before you continue reading. Or if you are up for a real challenge you can try to find a general method to solve the problem ^^
Solution
I think that viewing these flips as some kind of operations on a special rubik's cube gave me a better feel of the problem. We will first look at where a given element can move.
If we column flip an element at position (i,j) we arrive at (i,2n-j) if we column flip that we arrive at the same position, but it we row flip it we arrive at (2n-i,2n-j). Now let's start with a row flip on (i,j) we arrive at (2n-i,j) and similarly only a column flip will give us a new position (2n-i,2n-j). So from (i,j) we can only get to 3 other position (i,2n-j), (2n-i,j), (2n-i,2n-j). This means that the maximum from the main question cannot exceed the sum of the maximum over (i,2n-j), (2n-i,j), (2n-i,2n-j) where i,j ranges over the positions of the top left n by n array. Now if we can prove that the sum of the maximum over (i,2n-j), (2n-i,j), (2n-i,2n-j) is attained we are done.
We will show that this maximum is attained. Flipping rows and columns we can get the maximal element at (n-1,n-1) which is the right bottom corner of the upper left n by n matrix (my indexing starts from 0). As soon as we put something in that position we need to be careful because flipping the nth row or nth column will mess up that maximum. So let's try to get the maximal elements in place in the 3 positions around (n-1,n-1).
(n-2,n-1): Suppose that the maximum is at one of these positions: (n,n+2), (n+2,n), (n+2,n+2). Observe that we only need flips at n+2 row or column we we can leave the (n-1,n-1) intact.
(n-2,n-2) & (n-1,n-2): This is a bit tricky because we need to get these right at the same time. Flips at n-1 messes up (n-1,n-1) and row flip at n-2 messes up (n-2,n-1) so we can only column flip at n-2. Let's draw some picture. Below in red are the maximum values over the 4 possible positions. We first get (n-2,n-2) in the right position. The possible position which it can move over are indicated in green.
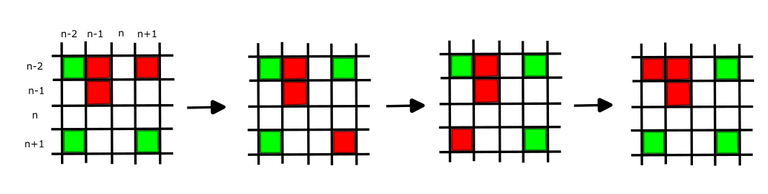
Observe that in the above process we encounter all possible values that the maximum corresponding to (n-2,n-2) can be at. A now for the final one (n-1,n-2). We introduced a new red block where the maximum value is at and green for all the possible positions it can move over.
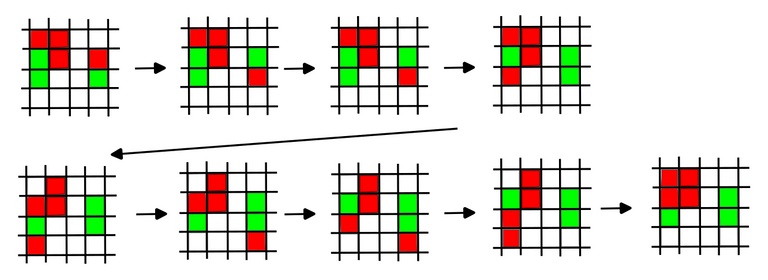
There is a tricky part in the second row where we have to move out the (n-2,n-2) to get the right value in at (n-1,n-2). It is a bit like solving a rubik's cube.
The above argument extends iteratively to the whole top right n by n block but I will leave that as an exercise. Of course I would love to know if anybody has a simpler derivation for the optimal strategy!
Congratulations @mathowl! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 400 posts.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Check out our last posts:
Support the HiveBuzz project. Vote for our proposal!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
The math is way beyond me, but the cat seems to follow 😇
=^..^=
damn
you are also still here :0
(you might only remember under my last acc @luegenbaron )
I have been on and off hive. Actually more off than on in the last 2 years :P